devbox
不正经
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

数据结构之红黑树（C++实现）_c++实现红黑树

作者：不正经 | 2024-05-19 16:25:20

赞

踩

c++实现红黑树

数据结构之红黑树

我之前的博客已经介绍过了二叉树和AVL树的基本概念和简单实现，具体参考数据结构-树（C语言实现篇）和数据结构之AVL树（C++实现）。

1. 红黑树

1.1 红黑树的概念

红黑树也是一种二叉搜索树，在此基础上每个结点增加一个存储位表示结点的颜色，可以是红色或者黑色，通过对任何一条从根节点到叶子结点的路径上每个结点颜色的限制，红黑树确保没有一条路径会比其他路径大一倍，因此，是接近平衡的一颗二叉搜索树。

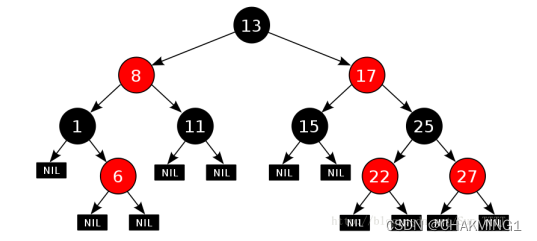
在这里插入图片描述

1.2 红黑树的性质
  1. 每个结点的颜色不是红色就是黑色。
  2. 根节点是黑色的。
  3. 如果一个节点是红色的，那么它的两个孩子结点是黑色的。
  4. 对于每个结点，从该结点到其所有后代的叶子结点的路径上，均包含相同数目的黑色结点。
  5. 每个叶子结点都是黑色的**（指的是空节点）**。

2. 红黑树的实现

2.1 红黑树结点的定义
// 结点的颜色
enum Colour {
    RED,
    BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;     // 左孩子
	RBTreeNode<K, V>* _right;   // 右孩子
	RBTreeNode<K, V>* _parent; // 父节点

	pair<K, V> _kv;  // 存储对
	Colour _col;      // 存储颜色

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
	{}
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
2.2 红黑树的插入操作

红黑树是在二叉搜索树的基础上加上了平衡限制条件，故分为两步：

  1. 按照二叉搜索树的规则插入新节点。

    typedef RBTreeNode<K, V> Node;
bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_col = BLACK; // 根节点必须为黑色
        return true;
    }
	
    // 按照二叉排序树的思路进行查找
    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    cur = new Node(kv);
    if (parent->_kv.first < kv.first)
    {
        parent->_right = cur;
    }
    else
    {
        parent->_left = cur;
    }

    cur->_parent = parent;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43

  2. 检测新结点插入之后，红黑树的性质是否被破坏。

    因为新插入的结点默认是红色的，因此，如果双亲结点是黑色，则没有违反红黑树任何性质。如果插入结点的双亲结点是红色的，就违背了红色结点的两个孩子结点是黑色的的性质。针对不同的情况进行分析：

    • 情况一：cur为红色，parent为红色，grandfather为黑色，uncle为红色。

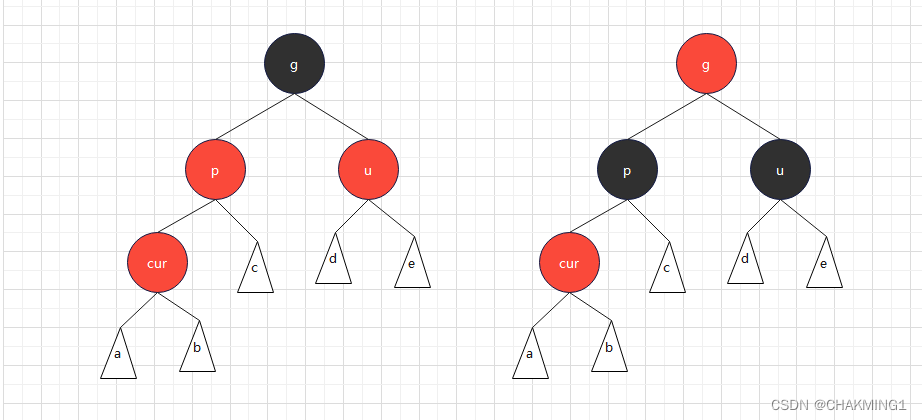
在这里插入图片描述

 设置双亲结点和双亲的兄弟结点为黑色。
 如果g结点为根节点，那么设置为黑色。因为根节点必须是黑色。
 如果g结点不为根节点，那么设置为红色，然后继续向上调整。

  • 1
  • 2
  • 3
  • 情况二：cur为红色，parent为红色，grandfather为黑色，uncle不存在/存在且为黑色。

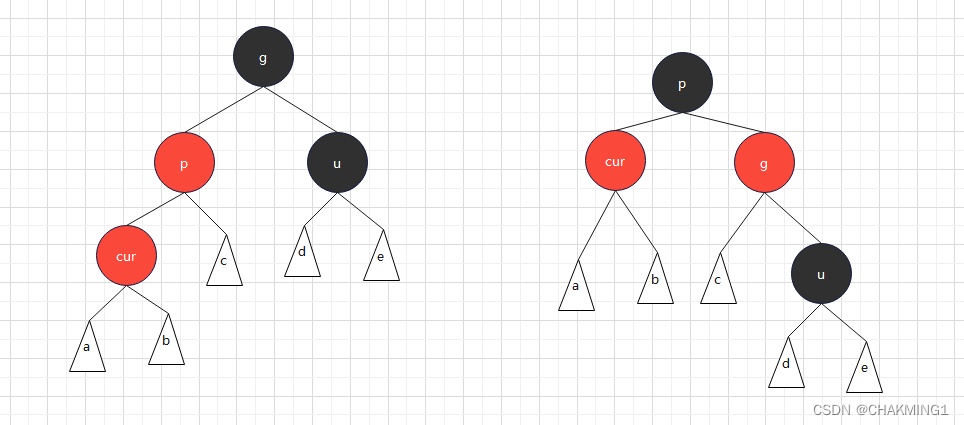
在这里插入图片描述
说明：（u结点分两种情况）

 如果u结点不存在，则cur一定是新插入的结点，因为cur和p都为红色，故冲突发生在这里，一定是有一个结点不满足，才会导致性质失效。
 如果u结点存在，则其一定是黑色的，那么cur结点原来的颜色也是黑色的，因为如果cur原来不是黑色的，就不满足从根节点到叶子结点的黑色节点数量相同。现在看到是黑色的原因在于cur的子树在调整过程中将cur结点的颜色从黑色改为红色。
 p结点为g结点的左孩子，cur结点为p结点的左孩子，进行右单旋。
 p结点为g结点的右孩子，cur结点为p结点的右孩子，进行左单旋。
 p结点变成黑色，g结点变成红色。

  • 1
  • 2
  • 3
  • 4
  • 5
  • 情况三：cur为红色，parent为红色，grandfather为黑色，uncle不存在/存在且为黑色。
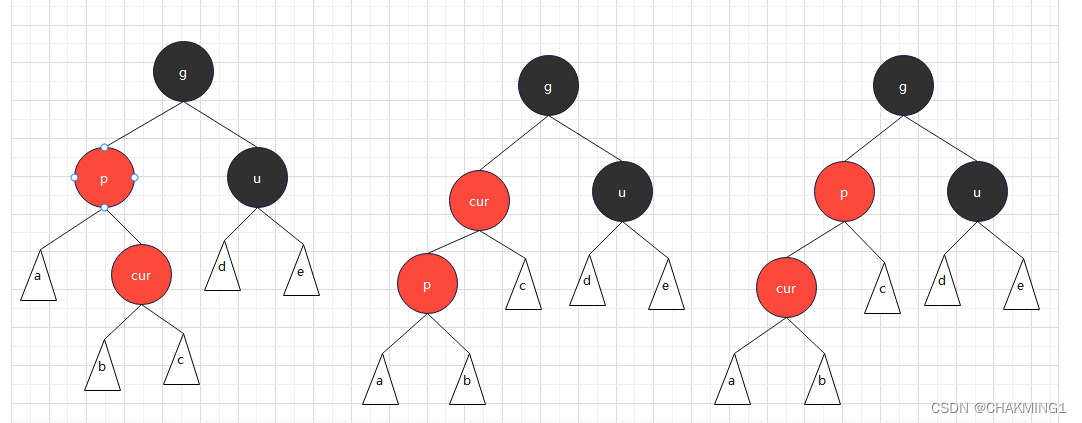
    在这里插入图片描述
p结点为g结点的左孩子，cur结点为p的右孩子，则对p做左单旋。
p结点为g结点的右孩子，cur结点为p的左孩子，则对p做右单旋。
最终变成了情况二，按照情况二接着处理即可。

  • 1
  • 2
  • 3

  1. 代码实现：

    // parent为红色
while (parent && parent->_col == RED)
{
    Node* grandfater = parent->_parent;
    assert(grandfater);
    assert(grandfater->_col == BLACK); // 如果爷爷的颜色不为黑色，那么前面的操作有误
    // 关键看叔叔
    // 若p为g左子树
    if (parent == grandfater->_left)
    {
        Node* uncle = grandfater->_right;
        // 情况一 : uncle存在且为红，变色+继续往上处理
        // 情况一只用变色，不需要旋转
        if (uncle && uncle->_col == RED)
        {
            parent->_col = uncle->_col = BLACK;
            grandfater->_col = RED;
            // 继续往上处理
            cur = grandfater;
            parent = cur->_parent;
        }// 情况二+三：uncle不存在 + 存在且为黑
        else
        {
            // 情况二：右单旋+变色
            //     g 
            //   p   u
            // c
            if (cur == parent->_left)
            {
                RotateR(grandfater); // 采用AVL树的旋转策略
                parent->_col = BLACK;
                grandfater->_col = RED;
            }
            else
            {
                // 情况三：左右单旋+变色
                //     g 
                //   p   u
                //     c
                RotateL(parent);  // 这一步结束后变成了情况二
                RotateR(grandfater); 
                cur->_col = BLACK;
                grandfater->_col = RED;
            }
			// 不需要在往上调整
            break;
        }
    }
    else // (parent == grandfater->_right)
    {
        Node* uncle = grandfater->_left;
        // 情况一
        if (uncle && uncle->_col == RED)
        {
            parent->_col = uncle->_col = BLACK;
            grandfater->_col = RED;
            // 继续往上处理
            cur = grandfater;
            parent = cur->_parent;
        }
        else
        {
            // 情况二：左单旋+变色
            //     g 
            //   u   p
            //         c
            if (cur == parent->_right)
            {
                RotateL(grandfater);
                parent->_col = BLACK;
                grandfater->_col = RED;
            }
            else
            {
                // 情况三：右左单旋+变色
                //     g 
                //   u   p
                //     c
                RotateR(parent);
                RotateL(grandfater);
                cur->_col = BLACK;
                grandfater->_col = RED;
            }
            break;
        }
    }
}

// 记得最后需要将根节点设置为黑色
_root->_col = BLACK;

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
2.3 红黑树的验证

红黑树的验证分为两步：

  1. 检测其是否满足二叉搜索树（中序序列是否是有序序列）。

    void InOrder()
{
    _InOrder(_root);
    cout << endl;
}

void _InOrder(Node* root)
{
    if (root == nullptr)
    {
    	return;
    }

    _InOrder(root->_left);
    cout << root->_kv.first << ":" << root->_kv.second << endl;
    _InOrder(root->_right);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17

  2. 检测是否满足红黑树的性质。

    bool IsBalance() 
{
    /* 性质：
        1. 根节点是黑色的
        2. 如果一个节点是红色的，则它的两个孩子结点是黑色的
        3. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
        4. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
     */
    if (_root == nullptr)
        return true;
    if (_root->_col == RED) {
        cout << "根节点不是黑色" << endl;
        return false;
    }
    // 黑色节点数量基准值
    int benchmark = 0;
    return PrevCheck(_root, 0, benchmark);
}

/*
	思路：
	判断每条路径上的黑色节点个数是否相同。
	blackNum为当前路径结点的个数
	benchmark第一次为0，第二次为第一次获取路径结点的个数
	如果benchmark不等于blackNum，表示当前路径的黑色节点个数与其他路径不相同，则不满足红黑树的条件。
*/
bool PrevCheck(Node *root, int blackNum, int &benchmark) 
{
    if (root == nullptr) {
        if (benchmark == 0) {
            benchmark = blackNum;
            return true;
        }

        if (blackNum != benchmark) {
            cout << "黑色节点数量不相等" << endl;
            return false;
        } else {
            return true;
        }
    }
    // 如果为黑色，那么黑色节点数量++
    if (root->_col == BLACK)
        ++blackNum;
	
    // 检查当前结点与其双亲结点是否都为红色
    if (root->_col == RED && root->_parent->_col == RED) {
        cout << "出现连续的红色结点" << endl;
        return false;
    }
    return PrevCheck(root->_left, blackNum, benchmark)
        && PrevCheck(root->_right, blackNum, benchmark);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
2.4 红黑树的删除

红黑树的删除这里不做讨论，有兴趣可以参考：《算法导论》或者《STL源码剖析》

https://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html

2.5 红黑树与AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(log_2(n))，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/不正经/article/detail/593691
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号