CVPR2023：BiFormer阅读笔记

前言

BiFormer是CVPR2023的一篇文章，文中提出自注意力机制作为Transformer的核心模块，可以帮助网络捕捉长距离上下文依赖，但是这种结构也有两个缺点：

1. 内存占用大
2. 计算代价高

有许多研究针对上述缺点进行优化：

1. 将注意力操作局限在局部窗口内，如图（b）。例如：Swin transformer
2. 将注意力操作局限在横向条纹内，如图（c）。
3. 将注意力操作局限在空洞窗口内，如图（d）。

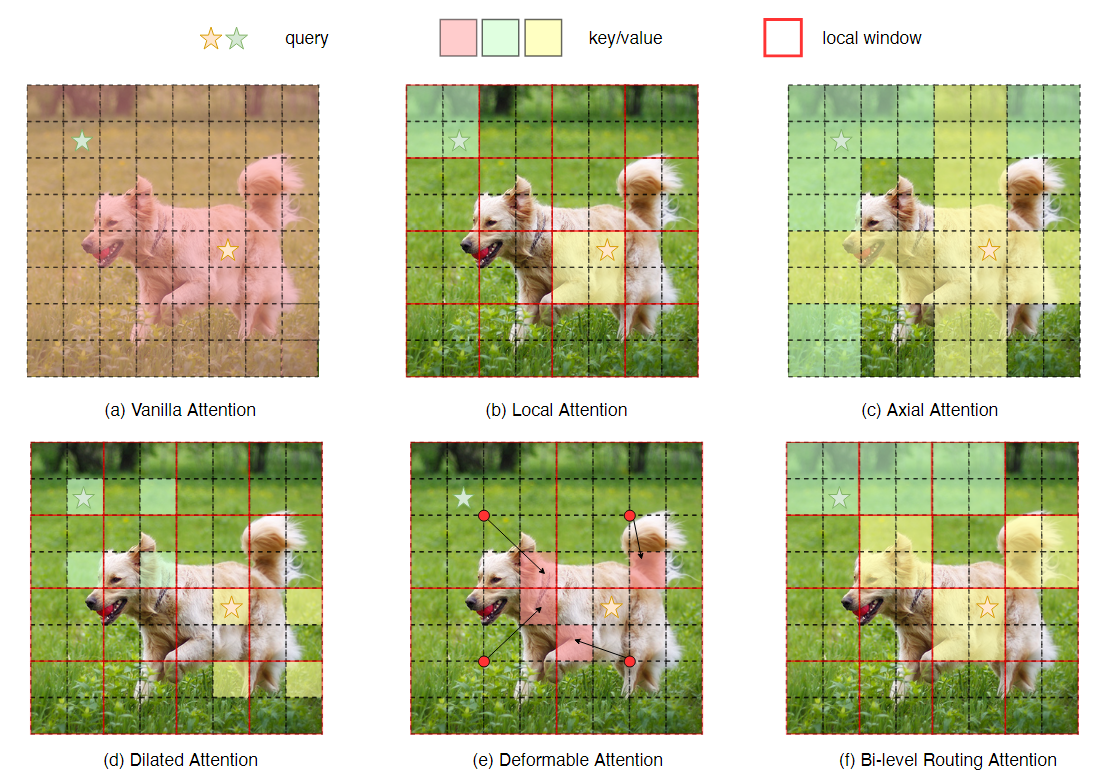
然后上述研究有两个共性的问题：

1. 使用手工制作的静态模式（无法自适应）
2. 所有Query共享相同的K / V对（无法做到互不干扰）

与上述研究不同，作者提出了一种新的动态稀疏注意力机制，通过双层路由来实现更灵活的算力分配，让每个Query处理语义上最相关的K-V对的一小部分。在此基础上，提出的BiFormer具有良好的性能和较高的计算效率。如图（f）。

计算复杂度由原来的$o((HW{)}^2)$降到了$o((HW{)}^{\frac{4}{3}})$。

1. 模型的特点

为了让每个Query处理语义上最相关的K-V对，首先面临的问题就是如何找到这些需要关注的K-V对。

一种方法是逐一为每个Query选择K-V对，那么就需要计算所有Query和所有Key之间的相关性，复杂性和原来的自注意力机制就相同了。

另一种方法是基于每个Query的局部上下文来预测注意力偏移量，如图（e），这虽然降低了计算复杂性，但会影响长距离依赖关系的建模。

为了解决这个问题，作者提出双层路由注意力机制（Bi-level Routing Attention, BRA）。核心思想是先在粗粒度区域级别过滤掉最不相关的键-值对，然后再去计算剩下的区域中的token-to-token注意力。

首先构造一个区域级关联图，然后对其进行修剪，使每个节点只保留前k个连接。因此每个区域只需要关注前k个路由区域。确定了参与区域后，下一步是应用token-to-token的注意，这是非常重要的，因为现在假定键值对在空间上是分散的。

2. 双层路由注意力机制（BRA）

输入一张图片，$X\in {\mathbb{R}}^{H\times W\times C}$，首先将其划分为$S\times S$个不同的区域，其中每个区域包含$\frac{HW}{S^2}$个特征向量。即将$X$变为$X^r\in {\mathbb{R}}^{S^2\times \frac{HW}{S^2}\times C}$

然后，通过线性映射获得$Q,K,V\in {\mathbb{R}}^{S^2\times \frac{HW}{S^2}\times C}$

$$Q=X^r{W}^q,K=X^r{W}^k,V=X^r{W}^v$$

其中，$W^q,W^k,W^v\in {\mathbb{R}}^{C\times C}$分别是query，key，value的投影权重。

使用有向图的region-to-region路由

通过构造一个有向图来找到每个给定区域应该参与的区域。

首先计算每个区域中Q和K的平均值，得到$Q^r,K^r\in {\mathbb{R}}^{S^2\times C}$

然后计算$Q^r$和$K^r$的区域间相关性的邻接矩阵：

$$A^r=Q^r(K^r{)}^T$$

然后只保留每个区域的前k个连接来修剪相关性图。有路由索引矩阵$I_r\in {\mathbb{N}}^{S^2\times k}$，逐行保存前k个连接的索引。

$$I^r=topkIndex(A^r)$$

$I^r$的第i行包含第i个区域的前k个最相关区域的索引。

token-to-token的注意力机制

利用区域到区域路由索引矩阵$I_r$，我们可以计算细粒度的token-to-token注意力 。对于区域i中的每个Query token，它将关注k个路由区域的并集中的所有键-值对，索引为$I_{(i,1)}^r,I_{(i,2)}^r,\dots ,I_{(i,k)}^r$。然而，要有效地实现这一步骤并不容易，因为这些路由区域将分散在整个特征图中，而GPU依赖于一次加载数十个连续字节的块的合并内存操作。因此，我们首先聚集key和value的tensor，即，

$$K^g=gather(K,I^r),V^g=gather(V,I^r)$$

其中，$K^g$和$V^g$是聚集后的key和value的tensor，然后对聚集后的K-V对使用注意力操作：

$$O=Attention(Q,K^g,V^g)+LCE(V)$$

此处，引入了一个局部上下文增强项$LCE((V))$，如论文Shunted Self-Attention via Multi-Scale Token Aggregation中所述。函数$LCE(\cdot )$用深度可分离卷积进行参数化，我们将卷积核大小设置为5。

3. BiFormer的结构

BiFormer结构如下图所示。

在第i个stage中，使用重叠的patch embedding（i=1时）或使用patch merging（i=2,3,4时）模块来降低输入空间分辨率，同时增加通道数量。然后使用使用$N_i$个相连的BiFormer块来对输入特征进行transformer操作。

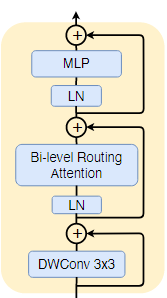
BiFormer块的细节结构如下图。先使用$3\times 3$卷积隐式编码相对位置信息。然后，依次使用BRA模块和一个2层的膨胀率为e的MLP模块进行跨位置关系建模和逐位置嵌入。

作者通过缩放网络宽度(即基本通道的数量$C$)和深度(即每个阶段使用的BiFormer块的数量$N_i,i=1,2,3,4$)，实例化了3个不同大小的BiFormer，如下表所示。其他结构保持一致。我们将每个注意力头设为32个通道，MLP扩展比e=3。对于BRA，由于输入分辨率不同，4个阶段我们使用$topk=1,4,16$，区域划分因子S = 7/8/16进行分类/语义分割/目标检测任务。