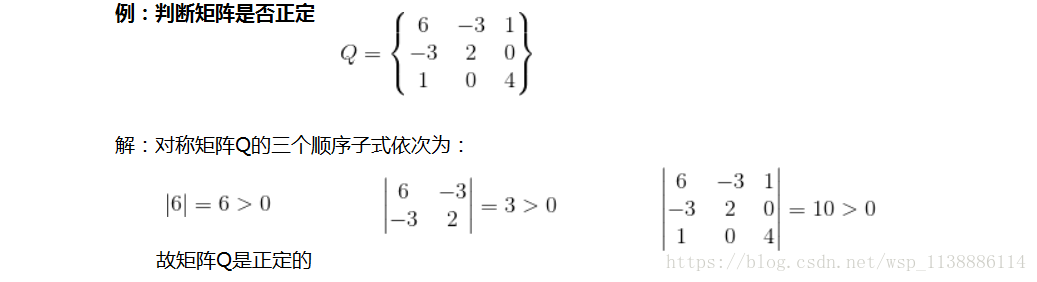协方差矩阵—Hessian矩阵—正定矩阵

一、基本概念

1.1 协方差矩阵 及推导

在统计学中用标准差描述样本数据的 “散布度” 公式中之所以除以 n-1 而不是 n,
是因为这样使我们以较少的样本集更好的逼近总体标准差。即统计学上所谓的 “无偏估计”。
关于 协方差 与 散度 ：https://blog.csdn.net/wsp_1138886114/article/details/80967843

方差：$$var(X)=\frac{{\sum }_{i=1}^n(X_i-\bar{X})(X_i-\bar{X})}{n-1}$$

各个维度偏离其均值的程度，协方差：$$\text{cov}(X,Y)=\frac{{\sum }_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{n-1}$$

协方差矩阵的计算：

c o v ( z ) = ( 1 2 3 4 3 4 1 2 2 3 1 4 ) j cov(z) =

$$\begin{pmatrix} 1 & 2 &3 &4 \\ 3&4 &1 & 2\\ 2& 3& 1& 4 \end{pmatrix}$$ j cov(z)=⎝⎛​132​243​311​424​⎠⎞​j

1.2 Hessian矩阵

Hessian矩阵定义：
若一元函数 $f(x)$ 在$x=x^{(0)}$ 点的某个领域内具有任意阶导数，则 $f(x)$ 在$x^{(0)}$ 点的泰勒展开式为：
$$f(x)=f(x^{(0)})+f^{\prime }(x^{(0)})\Delta x+\frac{1}{2}{f}^{\prime \prime }(x^{(0)})(\Delta x^2)+\cdots \text{\hspace{1em}(1)}$$

其中：$\Delta x=x-x^{(0)},\Delta x^2=(x-x^{(0)}{)}^2$

二元函数 $f(x_1,x_2)$在$X^{(0)}(x_1^{(0)},x_2^{(0)})$点处的泰勒展开式为：
$$\frac{1}{2}\left[\frac{{\partial }^{2}f}{{\partial }^2{x}_1^2}{|}_{x^{(0)}}\Delta x_1^2+2\frac{{\partial }^{2}f}{\partial x_1\partial x_2}{|}_{x^{(0)}}\Delta x_1\Delta x_2+\frac{{\partial }^{2}f}{{\partial }^2{x}_2^2}{|}_{x^{(0)}}\Delta x_2^2\right]+\cdots \text{\hspace{1em}(2)}$$

其中：$\Delta x_1=x_1-x_1^{(0)},\Delta x_2=x_2-x_2^{(0)}$

将上述(2)展开式写成矩阵形式，则有：
f ( X ) = f ( X ( 0 ) ) + ( ∂ f ∂ x 1 , ∂ f ∂ x 2 ) x ( 0 ) ( Δ x 1 Δ x 2 ) + 1 2 ( Δ x 1 , Δ x 2 ) { ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 } ∣ x ( 0 ) ( Δ x 1 Δ x 2 ) + ⋯ (3) f(X) = f(X^{(0)})+\left ( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2} \right )_{x^{(0)}}

$$\begin{pmatrix} \Delta x_1\\ \Delta x_2 \end{pmatrix}$$ +\frac{1}{2}(\Delta x_1,\Delta x_2) $$\begin{Bmatrix} \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1 \partial x_2}\\ \frac{\partial^2f}{\partial x_2 \partial x_1}& \frac{\partial^2f}{\partial x_2^2} \end{Bmatrix}$$ |_{x^{(0)}} $$\begin{pmatrix} \Delta x_1\\ \Delta x_2 \end{pmatrix}$$ +\cdots \tag{3} f(X)=f(X(0))+(∂x1​∂f​,∂x2​∂f​)x(0)​(Δx1​Δx2​​)+21​(Δx1​,Δx2​){∂x12​∂2f​∂x2​∂x1​∂2f​​∂x1​∂x2​∂2f​∂x22​∂2f​​}∣x(0)​(Δx1​Δx2​​)+⋯(3)

即为：
$$f(X)=f(X^{(0)})+\nabla f(X^{(0)}{)}^T+\frac{1}{2}\Delta x^{T}G(X^{(0)})\Delta X+\cdots \text{\hspace{1em}(4)}$$

其中：
G ( X ( 0 ) ) = { ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 } ∣ x ( 0 ) ,    Δ X = ( Δ x 1 Δ x 2 ) G(X^{(0)}) =

$$\begin{Bmatrix} \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1 \partial x_2}\\ \frac{\partial^2f}{\partial x_2 \partial x_1}& \frac{\partial^2f}{\partial x_2^2} \end{Bmatrix}$$ |_{x^{(0)}}, ~~\Delta X = $$\begin{pmatrix} \Delta x_1\\ \Delta x_2 \end{pmatrix}$$ G(X(0))={∂x12​∂2f​∂x2​∂x1​∂2f​​∂x1​∂x2​∂2f​∂x22​∂2f​​}∣x(0)​,  ΔX=(Δx1​Δx2​​)

$G(X^{(0)})$是 $f(x_1,x_2)$ 在 $X^{(0)}$ 点处的Hessian矩阵。它是由函数 $f(x_1,x_2)$ 在 $X^{(0)}$点处的二阶偏导数所组成的方阵。我们一般将其表示为:

H ( f ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] H(f) =

$$\begin{bmatrix} \frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2f}{\partial x_1 \partial x_n} \\ \frac{\partial^2f}{\partial x_2 \partial x_1} & \frac{\partial^2f}{\partial x_2^2} & \cdots & \frac{\partial^2f}{\partial x_2 \partial x_n}\\ \vdots & \vdots & \ddots &\vdots \\ \frac{\partial^2f}{\partial x_n \partial x_1} & \frac{\partial^2f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2f}{\partial x_n^2} \end{bmatrix}$$ H(f)=⎣⎢⎢⎢⎢⎢⎡​∂x12​∂2f​∂x2​∂x1​∂2f​⋮∂xn​∂x1​∂2f​​∂x1​∂x2​∂2f​∂x22​∂2f​⋮∂xn​∂x2​∂2f​​⋯⋯⋱⋯​∂x1​∂xn​∂2f​∂x2​∂xn​∂2f​⋮∂xn2​∂2f​​⎦⎥⎥⎥⎥⎥⎤​

简写成： Q H e s s i a n = [ I x x I x y I y x I y y ] \mathbf{Q_{Hessian}} =

$$\begin{bmatrix} I_{xx} & I_{xy}\\ I_{yx} & I_{yy} \end{bmatrix}$$ QHessian​=[Ixx​Iyx​​Ixy​Iyy​​]

1.3 Hessian矩阵 示例

1.3 正定矩阵定义及性质

在线性代数中，正定矩阵（positive definite matrix）简称正定阵。
定义：A是n阶方阵，如果对于任何非零向量x都有$x^{T}Ax>0$就称A正定矩阵。

1.4 正定矩阵 示例