1、线性回归模型

1、主要解决问题类型

1.1 预测分析（Prediction）

线性回归可以用来预测一个变量（通常称为因变量或响应变量）的值，基于一个或多个输入变量（自变量或预测变量）。例如，根据房屋的面积、位置等因素预测房价。

1.2 异常检测（Outlier Detection）

线性回归可以帮助识别数据中的异常值。异常值可能会影响回归模型的准确性，因此检测和处理异常值是线性回归分析的重要一环。

1.3 关联分析（Association）

线性回归可以帮助确定两个或多个变量之间的关系强度和方向。它可以显示自变量与因变量之间是正相关还是负相关，以及相关性的强度。

2、线性回归模型

2.1 什么是线性回归模型

模型表达式：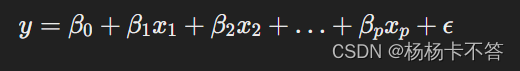

• y 是因变量（要预测的目标）
• x1,x2,…,xp 是自变量（特征或解释变量）
• β0,β1,…,βp 是模型的参数，表示因变量与自变量之间的影响关系
• ϵ 是误差项，表示模型无法解释的随机误差。

2.2 如何判断某个问题是否适合使用线性回归模型？

1. 线性关系假设：线性回归模型假设因变量与自变量之间的关系是线性的。因此，首先需要检验自变量和因变量之间是否存在大致的线性关系。可以通过绘制散点图观察变量之间的关系来初步判断。
2. 连续性和正态性假设：线性回归模型通常假设自变量和因变量是连续的，并且误差项 ϵ 是独立同分布的，并且服从正态分布。如果数据违反这些假设，可能需要考虑其他类型的模型。
3. 数据量：通常来说，线性回归对数据量的要求并不高，但是如果数据量非常少或者变量之间的关系非常复杂，可能需要考虑更复杂的模型。
4. 预测的需求：如果任务是预测一个连续的数值型目标变量，而且认为这些预测可以通过自变量的线性组合来实现，那么线性回归也是一个合适的选择。

2.3 NILM中的线性回归模型

2.3.1 负载识别问题

在NILM中，负载识别是一个核心问题，即通过总电力消耗数据来识别和分离出各个电器的能耗。线性回归模型可以应用于以下情况：

问题描述： 根据总电力消耗（因变量）和不同电器的特征（自变量，如电流波形、功率特征等），建立线性回归模型来预测每个电器的能耗。

实际案例： 假设我们有一个家庭的总电力消耗数据以及每个电器在不同时间段内的功率特征。我们可以利用线性回归模型来拟合这些数据，从而识别出在该家庭中运行的各种电器，比如冰箱、空调、洗衣机等。

求解过程如下

1. 数据的收集与准备

首先，我们需要收集如下数据：

• 总电力消耗数据： 在监测点（例如家庭电表）上采集的总电力消耗时间序列数据。
• 各个电器的特征数据： 这些特征数据可以包括电器的功率特性、波形数据（如电流波形）、电压特征等。这些数据通常是通过传感器或NILM系统采集的。

2. 模型设定

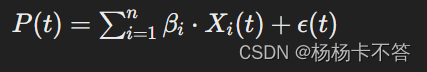
• P(t) 是在时刻 声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/人工智能uu/article/detail/761846