- 1SmsForwarder (短信转发器)无网络问题_短信转发器 不能转发
- 2AI作画的背后是怎么一步步实现的?一文详解AI作画算法原理+性能评测_ai绘画算法_ai绘图的原理
- 3力扣刷题笔记丨算法数据结构--链表--反转链表
- 4nginx(二十七)长连接和短连接_nginx tcp长链接代理
- 5NLP之MLP与CNN的姓氏分类实现
- 6数据结构与算法(七)(哈希表)_参考算法7.10,建立哈希表
- 7WebGL:基于web的交互式2D/3D图形引擎_基于 webgl2.0 设计二三维一体化的前端地图引擎
- 8Java获取resources下文件路径_jar包获取resource下的文件路径
- 9vmware workstation 各个版本官网下载链接_vmware workstation官网
- 10chatgpt赋能python:Python中如何快速有效地删除NaN值_去除数据中的nan
机器学习python实践——由特征选择引发的关于卡方检验的一些个人思考
赞
踩
最近在用python进行机器学习实践,在做到特征选择这一部分时,对于SelectPercentile和SelectKBest方法有些不理解,所以去了查看了帮助文档,但是在帮助文档的例子中出现了"chi2",没接触过,看过去就更懵了,查了一下资料知道"chi2"是在求卡方值,又没接触过,我整个人都裂了,但是还是耐着性子去查了资料,然后这篇文章主要想记录并分享一下关于卡方检验的一些个人思考,如果有误请见谅,欢迎大家一起前来探讨。当然,如果这篇文章还能入得了各位“看官”的法眼,麻烦点赞、关注、收藏,支持一下!
在引言中提到了SelectPercentile和SelectKBest所以先简单的啰嗦讲几句:
两个方法在我看来差不多,只不过一个是通过百分比来指定被选特征数量,一个是通过个数来指定被选特征数量,在帮助文档的例子中应该会看到 SelectKBest(chi2, k=2),这句语句的意思是我们将卡方值作为评分函数,然后选取分高的两个特征
特征选择的帮助文档的链接附上,有需要的小伙伴自取:1.13 特征选择-scikit-learn中文社区
下面我们进入正文,对卡方检验进行讲解:
一、卡方检验是什么?
个人感觉卡方检验主要是为了检验某个自变量/特征X和因变量/标签Y之间是否存在显著关系
二、卡方检验怎么做?
步骤1:先假定特征X与变量Y相互独立,即不存在显著关系
步骤2:根据上面假定算出理论值
步骤3:将理论值和观测值带入到Pearson公式中计算卡方值
步骤4:对计算出来的卡方值进行查表操作,以判断特征X和标签Y之间是否存在显著关系
三、独立样本2x2表格卡方检验计算举例
卡方值基本公式——Pearson公式:
![]()
其中A代表着实际值或观测值,T表示理论值或期望
步骤1没啥好讲的,就是一个假定,所以直接从步骤2开始,对于如何求解理论值,举个例子,大家感受一下,例子来源百度百科,相关链接大家有需要可以去文末自取。
假定我们要检验性别与化妆是否有关系,所以自变量X的定义域为{X1,X2}={化妆,不化妆},因变量Y的值域为{Y1,Y2}={男,女},我们用一个2x2的表格表示,即如下所示:
PS:表格中的括号外的数据为观测值,括号内的数据为理论值
| Y1:男 | Y2:女 | 行总计 | |
| X1:化妆 | 15(55) | 95(55) |
|
| X2:不化妆 | 85(45) | 5(45) |
|
| 列总计 |
|
|
|
表中15表示抽样时,男生化妆的数量,95表示女生化妆的数量,85表示男生不化妆的数量,5表示女生化妆的数量
先给出理论值公式:
![]()
其中![]() 表示X=Xi,Y=Yj的理论值,即第i行j列的理论值;
表示X=Xi,Y=Yj的理论值,即第i行j列的理论值;![]() 表示第i行总计,
表示第i行总计,![]() 表示第j列总计
表示第j列总计
将上述表格的数据带入到理论值公式中,就可以得到理论值,如下所示:
![]()
![]()
![]()
![]()
将所有的观测值和理论值带入到Pearson公式中,就可以得到卡方值,如下所示:
![]()
其中![]() 表示X=Xi,Y=Yj的观测值,即第i行j列的观测值
表示X=Xi,Y=Yj的观测值,即第i行j列的观测值
我们对下表进行查询,在下表中k值最大为10.828,而卡方值为129.29,所以我们可以知道卡方值大于10.828的概率是0.1%,也就是说性别与化妆与否不存在显著关系的概率最大仅有0.1%,即性别与化妆显著存在显著关系的概率大于99.9%,所以性别与化妆显著存在显著关系
由此可知,卡方值越大,两个变量之间存在显著关系的概率越大

看到了上面的卡方值计算,可能大部分小伙伴都会觉得计算很复杂,那有没有简便的速算公式去直接套用呢?我的答案是:有!!!下面给出:
对于2x2的表格,即特征数=2,标签数=2的情况,卡方值的速算公式如下:
![]()
我们将上面性别与化妆与否是否存在显著关系的数据带入到速算公式中检验一下,看看是否正确
![]()
经过速算公式算出的卡方值也是129.29,与Pearson公式结果一致,所以可证速算公式是正确的
四、多独立样本RxC表格卡方检验计算举例
可能很多小伙伴已经发现了,上面的例子是一个很特殊的情况,自变量或者特征的值只有两个,因变量或者标签的值也只有两个,那如果自变量或者因变量的值不止两个该怎么办呢?
两种办法:
1、按照上面给出的Pearson公式,先算出理论值,再把理论值带入到卡方值的公式中计算;
2、采用独立样本RxC表格的速算公式进行计算,具体公式如下所示:
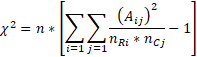
下面给出一个3x2表格卡方检验的例子,如下所示:
| 无效 | 有效 | 行总计 | |
| 外用膏药组 | 26(13.805) | 118(130.195) | 144 |
| 物理疗法组 | 7(19.748) | 199(186.252) | 206 |
| 药物治疗组 | 18(17.447) | 164(164.553) | 182 |
| 列总计 | 51 | 481 | 532 |
将所有的观测值和理论值带入到Pearson公式中,就可以得到卡方值,如下所示:
![]()
我们再用速算公式计算一下卡方值,如下所示:
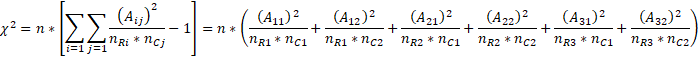
![]()
惊喜的发现速算公式算出来的结果和Pearson公式一致,所以可证速算公式是正确的
五、自由度说明
当然有些小伙伴在看一些相关资料的时候会看到自由度,我这边也简单的提一嘴,自由度的公式非常简单,如下所示:
![]()
以本文第一张表格和第三张表格为例,R代表表格中的行数,C代表表格中的列数,对于第一张表格R=C=2,对于第三张表格R=3,C=2
为啥要求自由度?——也是为了查表,只是查的不是本文中的第二张表,而是一张叫做“卡方分布临界值”的表,具体怎么用这个表,有兴趣的小伙伴可以查看下面的视频链接:
【统计科普】七分钟轻松掌握卡方检验 - 卡方拟合度检验、卡方独立性检验_哔哩哔哩_bilibili
六、数值型变量说明
在这里我必须先说明一下:卡方检验主要用于研究定类与定类数据之间的差异关系。
在上面的例子中都是一些字符串式的“类型特征”,通过上面的例子,我们也不难看出。但是,实际生活都是一群数值类型的“连续特征”,所以有些小伙伴就想强行用卡方检验来分析数值类型的“连续特征”,那么该如何处理呢?
如果想用卡方检验来分析数值类型的“连续特征”,其实也是不可以,只用将数据离散,然后分段即可,并且各段之间互不相交,再将每段看成一个类即可,有点类似“数据分箱”,比如说特征X,他的取值范围是(1,10),然后抽样十次,十次的结果是[1,2,3,4,5,6,7,8,9,4],我们将X分成两段,其中,第一段A1=(1,5],第二段A2=(5,10),之后将抽样结果按照每段的取值范围放入相应的段中即可,即A1:{1,2,3,4,4,5};A2:{6,7,8,9},然后我们将第一段A1看成类别1,将第二段A2看成类比2即可
七、应用条件
写到这里,有些乏了,不想手敲了,直接从网上截图

解释一下,样本含量对应本文中的n,理论频数对应本文中的![]()
矫正公式的话,大家可以去看一下下面的文章:
参考文章
卡方检验(Chi_square_test): 原理及python实现 - Leo_John - 博客园 (cnblogs.com)
卡方检验x2什么意思_卡方检验和方差分析-腾讯云开发者社区-腾讯云 (tencent.com)


