《算法设计与分析》第三章：动态规划_求将正整数n无序拆分成最大数为k(称为n的k拆分)的拆分方案个数,要求所有的拆分方

前言

更多动态规划内容可以参考本人其他相关博客，如下：

动态规划-背包问题详解
动态规划-线性Dp和区间Dp详解
动态规划-线性Dp进阶详解
动态规划-计数、数位统计、状态压缩、树形、记忆化搜索Dp

动态规划

适合动态规划求解的问题:

（1）具有最优子结构：原问题的最优解包含子问题的最优解
（2）有重叠子问题：子问题之间不独立，一个子问题在下一阶段决策中可能被多次使用到
（3）无后效性：某阶段状态一旦确定，就不受这个状态以后决策的影响

动态规划求解问题步骤：

（1）分析问题最优子结构，将大问题转换为小问题（状态转移）
（2）定义最优解（状态转移方程或递归方程，确定dp含义）
（3）以自底向上或自顶向下（备忘录法）方式填表或求解
（4）根据计算最优值时得到的信息，构造问题最优解

一、本章作业

1.子序列问题

子序列是字符串的若干字符（可能不连续，但前后关系不能变）构成的序列；子串是字符串的若干连续字符构成的序列。给定两个字符序列A和B：

（1）求两个序列的最长公共子序列的长度，并输出该子序列（输出一种即可）。

【DP数组含义】

• f[i][j]表示所有在第一个序列的前i个字母中出现，且在第二个序列的前j个字母中出现的子序列集合中，取最长公共子序列的长度值，即为f[i][j]的值

【状态转移方程】

• f[i][j] = max(f[i][j],f[i-1][j], f[i][j-1])
• 两个序列分别是a[i]、b[j]，我们则可以把f[i][j]分为四种情况，不包含a[i]不包含b[j]、不包含a[i]包含b[j]、包含a[i]不包含b[j]、包含a[i]包含b[j]
• 不包含a[i]包含b[j]：f[i-1][j]包含该种情况，该情况是f[i-1][j]的子集，因为f[i-1][j]可能包含b[j]也可能不包含b[j]（包含a[i]不包含b[j]同理）
• 包含a[i]包含b[j]：这种情况必须满足a[i] == b[j]，f[i-1][j-1]+1
• 不包含a[i]不包含b[j]：已经包含在f[i-1][j]里了

【算法实现与运行截图】

#include<bits/stdc++.h>

using namespace std;

const int Size = 1010;  
int c[Size][Size]; //dp数组
int b[Size][Size];    

int LCS_length(string X, string Y)
{
    int m = X.size();
    int n = Y.size();
    for(int i=1; i<=m; i++)
	{
		c[i][0] = 0;
	} 
	for(int j=1; j<=n; j++)
	{
		c[0][j] = 0;
	} 
    for(int i=1; i<=m; i++)
    {
        for(int j=1; j<=n; j++)
        {
            if(X[i-1] == Y[j-1]) 
            {
                c[i][j] = c[i-1][j-1] + 1;
                b[i][j] = 1;
            }
            else if(c[i-1][j] >= c[i][j-1])
            {
                c[i][j] = c[i-1][j];
                b[i][j] = 2;
            }
            else
            {
                c[i][j] = c[i][j-1];
                b[i][j] = 3;
            }
        }
    }
    return c[m][n]; //最长公共子序列的长度 
}
void LCS(string X, int i, int j)
{
    if(i==0 || j==0) return;
    if(b[i][j] == 1) 
    {
        LCS(X, i-1, j-1);
        cout<<X[i-1];  //a[i-1]==b[j-1]
    }
    else if(b[i][j]==2) LCS(X, i-1, j);
    else if(b[i][j]==3) LCS(X, i, j-1);
}
int main()
{
    string X, Y;
    cin>>X>>Y;
    cout<<"最大公共子序列长度为:"<<LCS_length(X, Y)<<endl;
    cout<<"最大公共子序列为:";
    LCS(X, X.size(), Y.size());
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

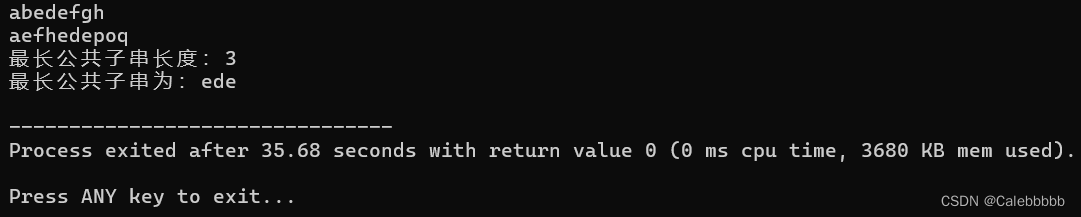
（2）求两个序列的最长公共子串的长度，并输出该子串（输出一种即可）。

【DP数组含义】

• f[i][j]表示所有在第一个序列且以a[i]结尾的子串，且在第二个序列且以b[i]结尾的子串，取最长公共子序列的长度值，即为f[i][j]的值

【状态转移方程】

• f[i][j] = max(f[i][j],f[i-1][j-1] + 1)

【算法实现与运行截图】

#include<bits/stdc++.h>

using namespace std;

int main()
{
	string s1,s2;
	cin>>s1>>s2;
	if(s1.size() > s2.size()) //以短的作为s1
		swap(s1,s2);
	int len1 = s1.size(), len2 = s2.size();
	int start = 0, mx = 0; //记录结果
	vector<vector<int> > dp(len1+1,vector<int>(len2+1,0));
	for(int i = 1;i<=len1;i++)
	{
		for(int j = 1;j<=len2;j++)
		{
			if(s1[i-1] == s2[j-1])
				dp[i][j] = dp[i-1][j-1] + 1;
			if(dp[i][j] > mx)
			{
				mx = dp[i][j];
				start = i - mx;
			}
		}
	}
	cout<<"最长公共子串长度："<<mx<<endl;
	cout<<"最长公共子串为："<<s1.substr(start,mx)<<endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.0-1背包问题

用动态规划求解0-1背包问题。输出放置哪几件物品使得背包价值最大？背包价值是多少？

【DP数组含义】

• f[i][j]表示在前i种物品种选取，使得容量不超过j，满足该情况的所有情况集合，在集合中选取最优解，该最优解的质量即为f[i][j]的值

【状态转移方程】

• f[i][j]=max(f[i-1][j-v[i]]+w[i],f[i-1][j])
• 优化为二维：f[j]=max(f[j],f[j-v[i]]+w[i])

【算法实现与运行截图】

#include <bits/stdc++.h>

using namespace std;

const int N=105;
int w[N]; //重量
int v[N]; //价值
int path[N][1005];//path[i][j] 
int dp[1005];  //dp[i][j]的优化

int main()
{ 
	int n,m;//商品件数和背包容量 ,要取得最大的价值 
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>w[i];
	}
	for(int i=1;i<=n;i++)
	{
		cin>>v[i];
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=w[i];j--)
		{
			path[i][j]=0;	
			if(dp[j-w[i]]+v[i]>dp[j])
			{
				path[i][j]=1;
				dp[j]=dp[j-w[i]]+v[i];
			}
		} 
	} 
	cout<<"最大背包价值："<<dp[m]<<endl;
	stack<int> st;
	int i=n;
	int j=m;
	while(i>0&&j>0)
	{
		if(path[i][j]==1)
		{	
			st.push(i);
			j-=w[i];
		}
		i--;
	}
	cout<<"所选物品：";
	while(!st.empty())
	{
		cout<<st.top()<<' ';
		st.pop();
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

3.设备分配问题

某企业根据计划安排，拟将n台相同的设备分配给m个子公司，各子公司获得这种设备后，可以盈利Cij(i台设备提供给j号子公司将得到的利润，1≤i≤n，1≤j≤m) 。问如何分配设备，才使这批设备利益最大化？

【DP数组含义】

• dp[i][j] 表示前 i 台设备分配给前 j 个子公司所能获得的最大利润

【状态转移方程】

• dp[i][j] = max(dp[i][j], dp[i - k][j - 1] + profit[k][j])

【算法实现与运行截图】

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 105;

int dp[MAXN][MAXN]; // dp[i][j] 表示前 i 台设备分配给前 j 个子公司所能获得的最大利润
int profit[MAXN][MAXN]; // 存储利润表，profit[i][j] 表示将 i 台设备分配给第 j 个子公司可以获得的利润

// 设备分配函数
int allocateDevices(int n, int m, vector<vector<int>>& c) 
{	
	// 根据提供的利润表，填充 profit 数组
	for (int i = 1; i <= n; ++i) 
	{
		for (int j = 1; j <= m; ++j) 
		{
			profit[i][j] = c[i][j];
		}
	}
	
	// 动态规划求解最大利润
	for (int i = 1; i <= n; ++i) 
	{
		for (int j = 1; j <= m; ++j) 
		{
			for (int k = 0; k <= i; ++k) 
			{
				dp[i][j] = max(dp[i][j], dp[i - k][j - 1] + profit[k][j]);
			}
		}
	}
	
	return dp[n][m]; // 返回最大利润
}

int main() 
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int n, m;
	cout << "请输入设备数量n和子公司数量m：" << endl;
	cin >> n >> m;
	
	vector<vector<int>> c(n + 1, vector<int>(m + 1, 0));
	cout << "请依次输入各个设备在各个子公司的利润：" << endl;
	for (int i = 1; i <= n; ++i) 
	{
		for (int j = 1; j <= m; ++j) 
		{
			cin >> c[i][j];
		}
	}
	
	int maxProfit = allocateDevices(n, m, c);
	cout << "最大利润为：" << maxProfit << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

4. 合唱队形问题

N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，而不改变其他同学的位置，使得剩下的K位同学排成合唱队形。合唱队形要求：设K位同学从左到右依次编号为1，2，…，K，他们的身高分别为T1,T2，…，TK，则他们的身高满足：
T1<…<Ti, 且Ti>Ti+1>…>TK(1<=i<=K)。
当给定队员人数N和每个学生的身高T[i]时，需要多少学生出列，可以得到最长的合唱队形。你也可以尝试输出需要出列哪些学生。

【算法思想】

• 用两个dp数组：l[i]代表从左开始以a[i]结尾的最长子序列长度为多少，r[i]代表从右开始以a[i]结尾的最长子序列长度为多少
• 从左到右遍历l：a[i]>a[j]&&sum<l[j]时，l[i] = l[j] + 1
• 从右到左遍历m：a[i]>a[j]&&sum<m[j]时，m[i] = m[j] + 1
• 最后将两者遍历相加取最大值即可

【算法实现与运行截图】

#include <bits/stdc++.h>

using namespace std;

const int N = 105;

int main()
{
	int n = 0;
	cin>>n;
	int a[N] = {0};
	int l[N] = {0};
	int m[N] = {0};
	for(int i = 0;i<n;i++)
	{
		cin>>a[i];
		l[i] = 1;
		m[i] = 1;
	}
		
	for(int i = 0;i<n;i++) 
	{
		int sum = INT_MIN;
		for(int j = 0;j<i;j++)
		{
			if(a[i]>a[j]&&sum<l[j])
			{
				sum = l[j];
				l[i] = l[j] + 1;
			}
		}
			
	}
		
	for(int i = n-1;i>=0;i--)
	{
		int sum = INT_MIN;
		for(int j = n-1;j>i;j--)
		{
			if(a[i] > a[j] && sum < m[j])
			{
				sum = m[j];
				m[i] = m[j] + 1;
			}
		}
	}
		
	int s = INT_MIN;
	for(int i = 0;i<n;i++)	
	{
		if(s<(l[i] + m[i] - 1) )
		{
			s = l[i] + m[i] - 1;
		}
	}
	cout<<n-s<<endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

【时空复杂度】

• 时间复杂度： O(n^2)
• 空间复杂度： O(N)

5. 石子合并问题

路边n堆石子排成一排，每堆石子个数不一。现要将石子有序地合并成一堆。规定每次只能选相邻的 2 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的耗费力气。试设计一个算法，计算将 n 堆石子合并成一堆的最省力气数。
例如有 4 堆石子分别为 1，3，5，2， 如果先合并 1、2 堆，代价为 4，得到 4，5，2；又合并 1，2 堆，代价为 9，得到 9，2 ；再合并得到 11，总代价为 4+9+11=24。如果第二步是先合并 2，3 堆，则代价为 7，得到 4，7，最后一次合并代价为 11，总代价为 4+7+11=22。

【算法思想】

• 状态表示：f[i][j]表示将第i堆石子和第j堆石子合并的所有方法的集合中，取代价最小值的最优解，f[i][j]的值即为该最小值
• 状态计算：可以从第i堆石子和第j堆石子合并方法的最后一次合并在何处后入手
• 利用前缀和：定义为数组s[N]
• 综上：f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1])

【算法实现与运行截图】

#include<bits/stdc++.h>

using namespace std;

const int N = 110,INF = 1e9;

int n;
int s[N];
int f[N][N];

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);
	
	for(int i = 1; i <= n; i ++ ) s[i] += s[i-1]; //计算前缀和
	
	for(int len = 2; len <= n; len ++ ) //遍历每种长度 
		for(int i = 1; i + len - 1 <= n; i ++ ) //遍历每种起点 
		{
			int l = i, r = i + len - 1;
			f[l][r] = INF;//初始化，全局变量初始值为0 
			
			for(int k = l; k < r; k ++ )
				f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l-1]);
		}
		
	printf("%d\n",f[1][n]);
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

【时空复杂度】

• 时间复杂度： O(n^3)
• 空间复杂度： O(N^2)

二、算法积累

1. 奇葩国家钞票问题

如果某奇葩国家的钞票面额分别是1、5、11，如何凑n元的面额，用张数尽量少的钞票？

• 状态表示：dp[i]凑i元的面额最少需要多少张钞票
• 状态计算：dp[i] = min(dp[i-1], dp[i-5],dp[i-11])

#include <bits/stdc++.h>

using namespace std;

const int MMM = 105;
const int INF = 0x3f3f3f3f;

int n;
int c1, c2, c3;
int dp[MMM];

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin >> n;
	
	for(int i = 1; i <= n; i ++ )
	{
		c1 = INF, c2 = INF, c3 = INF;
		if(i - 1 >= 0) c1 = dp[i - 1] + 1;
		if(i - 5 >= 0) c2 = dp[i - 5] + 1;
		if(i - 11 >= 0) c3 = dp[i - 11] + 1;
		dp[i] = min(min(c1, c2),c3);
	}
	
	cout << "所需纸币张数：" << dp[n] << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2. 组合数问题

求C_n^m，输入n和m，输出结果

• 状态表示：dp[i][j]表示C_i^j的结果
• 状态计算：dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]（排除i == j时等于1）

#include <bits/stdc++.h>

using namespace std;

const int MMM = 105;

int dp[MMM][MMM];

int ComB(int n, int m)
{
	for(int i = 1; i <= n; i ++ ) dp[i][0] = 1;
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			if(i == j) dp[i][j] = 1;
			else if(i > j) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
	
	return dp[n][m];
}

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	
	int n, m;
	cin >> n >> m;
	cout << ComB(n, m) << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

3. n的k分解问题

求将正整数n无序拆分成最大数为k（称为n的k拆分）的拆分方案个数，要求所有的拆分方案不重复

• 状态表示：f[i][j]表示i的j拆分方案数
• 状态计算：
  

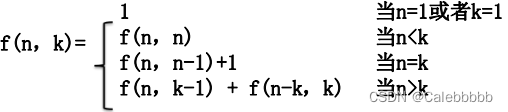
#include <bits/stdc++.h>

using namespace std;

const int MMM = 105;

int dp[MMM][MMM];

int Split(int n, int k)
{
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= k; j ++ )
		{
			if(i == 1 || j == 1) dp[i][j] = 1;
			else if(i < j) dp[i][j] = dp[i][i];
			else if(i == j) dp[i][j] = dp[i][j - 1] + 1;
			else if(i > j) dp[i][j] = dp[i][j - 1] + dp[i - j][j];
		}
	
	return dp[n][k];
}

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	
	int n, k;
	cin >> n >> k;
	cout << Split(n, k) << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

4. 矩阵连乘问题

给定n个矩阵｛A1,A2,…,An｝，其中，Ai与Ai+1是可乘的(i=1,2 ,…,n-1)。用加括号的方法表示矩阵连乘的次序，不同的计算次序计算量（乘法次数）是不同的，找出一种加括号的方法，使得矩阵连乘的次数最小。

• 状态表示：dp[i][j]表示矩阵连乘的最优值（所需乘法的最少次数）
• 状态计算：（设矩阵Ai的行分别为pi）
  

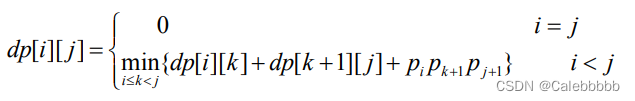
#include<bits/stdc++.h>

using namespace std;

const int MMM = 100;

int p[MMM];
int m[MMM][MMM],s[MMM][MMM];
int n;

void matrixchain()
{
	for(int r=2;r<=n;r++)//矩阵连乘的规模为r
	{
		for(int i=1;i<=n-r+1;i++)
		{
			int j=i+r-1;
			m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];//对m[][]开始赋值
			s[i][j]=i;//s[][]存储各子问题的决策点
			for(int k=i+1;k<j;k++)//寻找最优值
			{
				int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
				if(t < m[i][j])
				{
					m[i][j]=t;
					s[i][j]=k;
				}
			}
		}
	}
}

void print(int i,int j)
{
	if(i == j)
	{
		cout<<"A["<<i<<"]";
		return;
	}
	cout<<"(";
	print(i,s[i][j]);
	print(s[i][j]+1,j);//递归1到s[1][j]
	cout<<")";
}

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	
	cout<<"请输入矩阵的个数n : "<<endl;
	cin>>n;
	cout<<"请依次输入每个矩阵的行数和最后一个矩阵的列数："<<endl;
	for(int i=0;i<=n;i++) cin>>p[i];
	
	matrixchain(); 
	print(1,n);
	cout<<endl;
	
	cout<<"最小计算量的值为："<<m[1][n]<<endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

5. 整数分解问题

求将正整数n无序拆分的拆分方案个数，要求所有的拆分方案不重复

• 状态表示：f[i][j]表示i的j拆分方案数
• 状态计算：
  

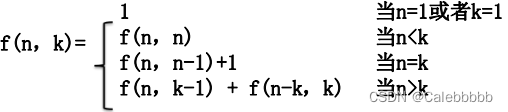
#include <bits/stdc++.h>

using namespace std;

const int MMM = 105;

int dp[MMM][MMM];

int Split(int n, int k)
{
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= k; j ++ )
		{
			if(i == 1 || j == 1) dp[i][j] = 1;
			else if(i < j) dp[i][j] = dp[i][i];
			else if(i == j) dp[i][j] = dp[i][j - 1] + 1;
			else if(i > j) dp[i][j] = dp[i][j - 1] + dp[i - j][j];
		}
	
	return dp[n][k];
}

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	
	int n;
	cin >> n ;
	cout << Split(n, n) << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

6. 字符串编辑距离问题

设A和B是两个字符串，现在要用最少的字符操作次数，将字符串A转换为字符串B。这里所说的字符操作包括3种：
（1）删除一个字符。
（2）插入一个字符。
（3）将一个字符替换另一个字符。
求将字符串A转换为字符串B的最少操作次数。
例如，A=“sfdqxbw”，B=“gfdgw”，结果为4。

• 状态表示：两个数组分别表示为a[N]、b[N]，则f[i][j]表示所有将a[1…i]变成b[1…j]的操作方式集合中，操作次数最少的方案，该方案的操作次数即为f[i][j]的值
• 状态计算：我们可以将f[i][j]的计算从其上一步来源出发，即a的最后一个元素a[i]要如何处理，分为三种情况：增、删、改（有条件）
  • 增：f[i][j-1]+1
  • 删：f[i-1][j]+1
  • 改：a[i]==b[j]则f[i-1][j-1]，a[i]!=b[j]则f[i-1][j-1]+1

#include<bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
	scanf("%d%s", &n, a + 1);
	scanf("%d%s", &m, b + 1);
	
	//初始化 
	for(int i = 0; i <= m; i ++ ) f[0][i] = i; //全增 
	for(int i = 0; i <= n; i ++ ) f[i][0] = i; //全删 
	
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
		{
			f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
			if(a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
			else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
		}
		
	printf("%d\n", f[n][m]);
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

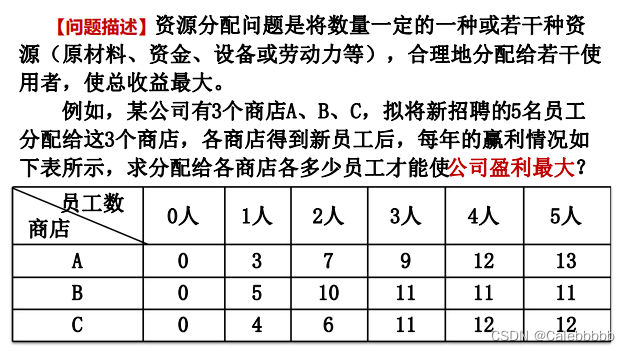
7.资源分配问题

• dp[i][j] 表示前 i 人分配给前 j 个商店所能获得的最大利润
• dp[i][j] = max(dp[i][j], dp[i - k][j - 1] + profit[k][j])

【算法实现与运行截图】

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 105;

int dp[MAXN][MAXN]; // dp[i][j] 表示前 i 台设备分配给前 j 个子公司所能获得的最大利润
int profit[MAXN][MAXN]; // 存储利润表，profit[i][j] 表示将 i 台设备分配给第 j 个子公司可以获得的利润

// 设备分配函数
int allocateDevices(int n, int m, vector<vector<int>>& c) 
{	
	// 根据提供的利润表，填充 profit 数组
	for (int i = 1; i <= n; ++i) 
	{
		for (int j = 1; j <= m; ++j) 
		{
			profit[i][j] = c[i][j];
		}
	}
	
	// 动态规划求解最大利润
	for (int i = 1; i <= n; ++i) 
	{
		for (int j = 1; j <= m; ++j) 
		{
			for (int k = 0; k <= i; ++k) 
			{
				dp[i][j] = max(dp[i][j], dp[i - k][j - 1] + profit[k][j]);
			}
		}
	}
	
	return dp[n][m]; // 返回最大利润
}

int main() 
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int n, m;
	cout << "请输入设备数量n和子公司数量m：" << endl;
	cin >> n >> m;
	
	vector<vector<int>> c(n + 1, vector<int>(m + 1, 0));
	cout << "请依次输入各个设备在各个子公司的利润：" << endl;
	for (int i = 1; i <= n; ++i) 
	{
		for (int j = 1; j <= m; ++j) 
		{
			cin >> c[i][j];
		}
	}
	
	int maxProfit = allocateDevices(n, m, c);
	cout << "最大利润为：" << maxProfit << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

8.最大连续子序列和

• 每次在原有基础加上当下元素值，小于0则置0，大于0则继续
• 每次和以前的最大和比较，取较大值

#include <bits/stdc++.h>

using namespace std ;

int main ( ) 
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	
	int n;
	cin >> n;
	int a[n + 1];
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	
	int ans = 0 , now = 0 ;
	
	for ( int i = 1 ; i <= n ; i++ ) 
	{
		now += a[i] ;
		if ( now < 0 ) now = 0 ;
		if ( ans < now ) ans = now ;  // 每次更新 ans 的值 ， 那么 ans 中存的一定是最大的元素和  
	}
	
	cout << ans << endl ;
	
	return 0 ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

9.最长递增子序列

• T(n)=O(n²)方法：
• 子序列并非指在连续的单元形成的子序列，可以不连续
• 状态表示：用f[i]表示状态，f[i]是指所有以第i个数结尾的上升子序列的集合中，取最长上升子序列，f[i]的值就是该最长上升子序列的长度值
• 状态计算：我们可以从上一个元素是什么入手，即从倒数第二个元素是什么入手，f[i]=max(f[j]+1),j=0,1,2,…,i-1
• 遍历计算后，在遍历一遍所有f[i]取最大值

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N],f[N]; //a[N]存所有元素，f[N]存所有状态 

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
	
	for(int i = 1; i <= n; i ++ )
	{
		f[i] = 1;
		for(int j = 1; j < i; j ++ )
			if(a[j] < a[i]) //只有该元素小于a[i]才符合逻辑 
				f[i] = max(f[i], f[j] + 1);
	}
	
	//遍历所有f[i] 
	int res = 0;
	for(int i = 1; i <= n; i ++ ) res = max(res, f[i]);
	
	printf("%d\n", res);
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

• T(n)=O(nlogn)方法：
• 采用二分法优化：改变dp[i]的含义：dp[i]表示长度为 i 的最长递增子序列末尾最小的数
• 例如：
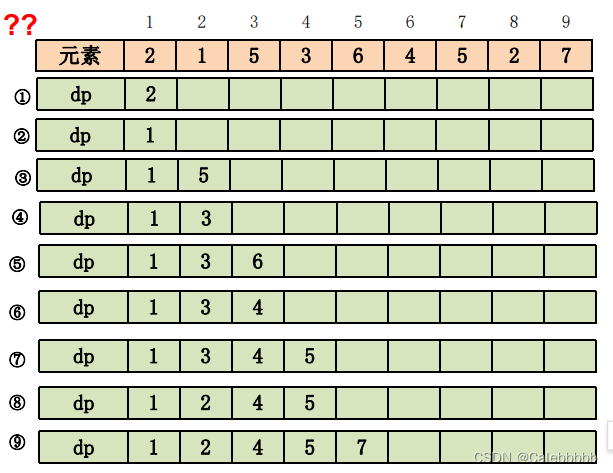
• 最后取dp数组长度即为最长递增子序列

#include <bits/stdc++.h>

using namespace std ;

const int MMM = 1e3 + 20;
const int inf = 0x3f3f3f3f;
int a[MMM];
int dp[MMM];
int n;

int BinarySearch(int dp[], int len, int x)
{
	int left = 1, right = len;
	while (left <= right)
	{
		int mid = (left + right) / 2;
		if (dp[mid] > x)
		{
			right = mid - 1;
		}
		else
		{
			left = mid + 1;
		}
	}
	return left;
}

int LIS(int n)
{
	dp[1] = a[1];
	int ans = 1;
	for(int i = 2; i <= n; i ++ )
	{
		if(a[i] > dp[ans])
		{
			ans ++;
			dp[ans] = a[i];
		}
		else
		{
			int temp = BinarySearch(dp, ans, a[i]);
			dp[temp] = a[i];
		}
	}
	return ans;
}

int main ( ) 
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	
	cin >> n;
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	
	fill(dp, dp + MMM, inf);
	int re = LIS(n);
	cout << re << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

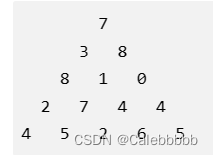
10.数字三角形

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

• 状态表示：用f[i][j]来表示状态，其中i表示第几行（从1开始），j表示第几斜列（从1开始），斜列是指从右上到左下的列，比如该题中7、3、8、2、4在第1斜列。则f[i][j]表示，从起点到a[i][j]的所有情况集合中，使得路径和最大的一种情况，其f[i][j]的值就是该路径和的值
• 状态计算：在该三角中，我们可以将f[i][j]的计算划分来源，分为从a[i][j]左上f[i-1][j-1]而来和从a[i][j]右上f[i-1][j]而来
• 所以综上：f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j])
• 在遍历计算后，遍历最后一行取最大值即可

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 510, INF = 1e9; //INF定义为无穷 

int n;
int a[N][N]; //存三角形每个数 
int f[N][N]; //存每个状态 

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= i; j ++ )
			scanf("%d", &a[i][j]);
	
	//状态全部初始化为负无穷，且边界外的一层也要做此处理
	//处理原因：a[i][j]可能是负数，而且边界外的一层有可能需要用到 
	for(int i = 0; i <= n; i ++ )
		for(int j = 0; j <= i + 1; j ++ )
			f[i][j] = -INF;
			
	f[1][1] = a[1][1];
	for(int i = 2; i <= n; i ++ )
		for(int j = 1; j <= i; j ++ )
			f[i][j] = max(f[i-1][j-1] + a[i][j], f[i-1][j] + a[i][j]);
			
	//遍历最后一行 
	int res = -	INF;
	for(int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
	
	printf("%d\n",res);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

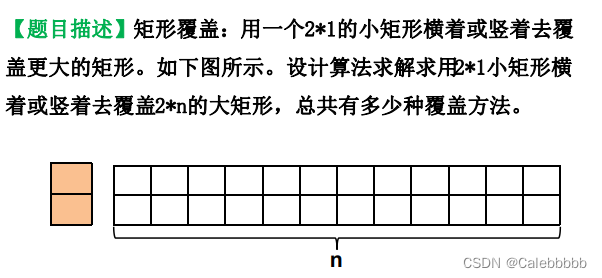
11.矩阵覆盖问题

• 思路：
  
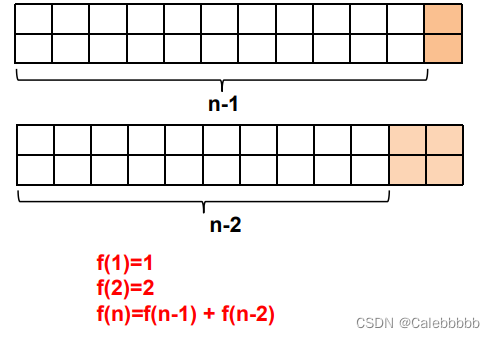
• 可以推广到多行

#include<bits/stdc++.h>

using namespace std;

int main()
{
	int n;
	cin >> n;
	int f[n + 10];
	f[1] = 1;
	f[2] = 2;
	for(int  i = 3; i <= n; i ++ )
	{
		f[i] = f[i - 1] + f[i - 2];
	}
	cout << f[n] << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

12.蒙德里安的梦

求把 N×M 的棋盘分割成若干个 1×2 的长方形，有多少种方案。
例如当 N=2，M=4时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。
如下图所示：

• 状态压缩Dp的核心思路就是将状态转化为二进制
• 此题行向摆放确定，则列向摆放确定，所以我们只需要考虑行向即可
• 状态表示：f[i][j]表示第i列的状态为j的所有方法数
• j二进制表示状态：j表示每一行是否为1*2条形块的第二个正方形元素
• j表示当前列状态，k表示上一列状态，存在必须满足的条件：（1）（j&k）== 0表示不会形成有重合部分的1*2条形块（2）j|k不存在连续奇数个0，表示第k层不会有奇数个空白列向元素（不符合摆放满标准）

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 12, M = 1 << N;

int n, m;
long long f[N][M];
bool st[M];

int main()
{
    while (cin >> n >> m, n || m)
    {
        for (int i = 0; i < 1 << n; i ++ )
        {
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; j ++ )
                if (i >> j & 1)
                {
                    if (cnt & 1) st[i] = false;
                    cnt = 0;
                }
                else cnt ++ ;
            if (cnt & 1) st[i] = false;
        }

        memset(f, 0, sizeof f);
        f[0][0] = 1;
        for (int i = 1; i <= m; i ++ )
            for (int j = 0; j < 1 << n; j ++ )
                for (int k = 0; k < 1 << n; k ++ )
                    if ((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];

        cout << f[m][0] << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

13.括号匹配

给一个字符串，里面只包含’(‘,’[‘,’{‘,’}‘,’]‘,’)'六种符号，请问需要至少添加多少个括号才能使这些括号匹配。

• 用一个栈来存储左侧括号
• 每一个右侧括号出现，都可以去栈顶匹配，不匹配则答案加一，并出栈，匹配则直接出栈
• 可以直接使用栈，不需要DP

#include <bits/stdc++.h>

using namespace std;

int minAddToMakeValid(string s) 
{
	stack<char> st;
	int count = 0;
	
	for(char c : s) 
	{
		if(c == '(' || c == '[' || c == '{') 
		{
			st.push(c);
		} 
		else 
		{
			if(st.empty()) 
			{
				count++; // 如果栈为空，表示没有左括号与之匹配，需要添加右括号
			} 
			else 
			{
				char top = st.top();
				st.pop();
				if((c == ')' && top != '(') || (c == ']' && top != '[') || (c == '}' && top != '{')) 
				{
					count++; // 如果栈顶左括号与当前右括号不匹配，需要添加右括号
				}
			}
		}
	}
	
	// 遍历完字符串后，栈中剩余的左括号需要添加右括号与之匹配
	count += st.size();
	
	return count;
}

int main() 
{
	string s;
	cout << "请输入只包含括号的字符串: ";
	cin >> s;
	
	int minAdd = minAddToMakeValid(s);
	cout << "至少需要添加 " << minAdd << " 个括号才能使括号匹配。" << endl;
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50