【YOLOv8改进】MSCA: 多尺度卷积注意力 (论文笔记+引入代码).md_yolov8中引入msca

YOLO目标检测创新改进与实战案例专栏

专栏目录： YOLO有效改进系列及项目实战目录 包含卷积，主干 注意力，检测头等创新机制 以及 各种目标检测分割项目实战案例

专栏链接: YOLO基础解析+创新改进+实战案例

摘要

我们提出了SegNeXt，一种用于语义分割的简单卷积网络架构。最近基于变换器的模型由于自注意力在编码空间信息方面的效率而在语义分割领域占据主导地位。在本文中，我们展示了卷积注意力是一种比变换器中的自注意力机制更高效和有效的编码上下文信息的方式。通过重新审视成功的分割模型所拥有的特征，我们发现了几个关键组件，这些组件导致了分割模型性能的提升。这激励我们设计了一种新颖的卷积注意力网络，该网络使用廉价的卷积操作。没有任何花哨的技巧，我们的SegNeXt在包括ADE20K、Cityscapes、COCO-Stuff、Pascal VOC、Pascal Context和iSAID在内的流行基准测试上，显著提高了先前最先进方法的性能。值得注意的是，SegNeXt超越了EfficientNet-L2 w/ NAS-FPN，在Pascal VOC 2012测试排行榜上仅使用1/10的参数就达到了90.6%的mIoU。平均而言，与最先进的方法相比，SegNeXt在ADE20K数据集上的mIoU提高了约2.0%，同时计算量相同或更少。

创新点

基本原理

MSCA 主要由三个部分组成：（1）一个深度卷积用于聚 合局部信息；（2）多分支深度卷积用于捕获多尺度上下文信息；（3）一个 1 × 1 逐点卷积用于模拟特征中不同通道之间的关系。1 × 1 逐点卷积的输出被直接用 作卷积注意力的权重，以重新权衡 MSCA 的输入。

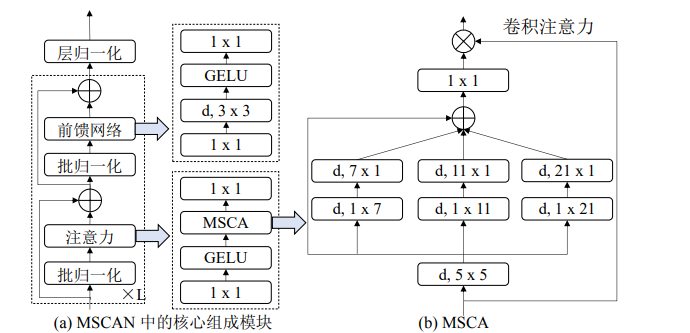
MSCA 可以写成 如下形式：其中 F 代表输入特征，Att 和 Out 分别为注意力权重和输出，⊗ 表示逐元素的矩 阵乘法运算，DW­Conv 表示深度卷积，Scalei (i ∈ {0, 1, 2, 3}) 表示上图右边侧图中的第 i 个分支，Scale0 为残差连接。遵循[130]，在 MSCA 的每个分支中，SegNeXt 使用两个深度条带卷积来近似模拟大卷积核的深度卷积。每个分支的卷积核大 小分别被设定为 7、11 和 21。 选择深度条带卷积主要考虑到以下两方面原 因：一方面，相较于普通卷积，条带卷积更加轻量化。为了模拟核大小为 7 × 7 的标准二维卷积，只需使用一对 7 × 1 和 1 × 7 的条带卷积。另一方面，在实际 的分割场景中存在一些条状物体，例如人和电线杆。因此，条状卷积可以作为 标准网格状的卷积的补充，有助于提取条状特征。

yolov8 引入

class MSCAAttention(BaseModule):
   """Attention Module in Multi-Scale Convolutional Attention Module (MSCA).

   Args:
       channels (int): The dimension of channels.
       kernel_sizes (list): The size of attention
           kernel. Defaults: [5, [1, 7], [1, 11], [1, 21]].
       paddings (list): The number of
           corresponding padding value in attention module.
           Defaults: [2, [0, 3], [0, 5], [0, 10]].
   """

   def __init__(self,
                channels,
                kernel_sizes=[5, [1, 7], [1, 11], [1, 21]],
                paddings=[2, [0, 3], [0, 5], [0, 10]]):
       super().__init__()
       self.conv0 = nn.Conv2d(
           channels,
           channels,
           kernel_size=kernel_sizes[0],
           padding=paddings[0],
           groups=channels)
       for i, (kernel_size,
               padding) in enumerate(zip(kernel_sizes[1:], paddings[1:])):
           kernel_size_ = [kernel_size, kernel_size[::-1]]
           padding_ = [padding, padding[::-1]]
           conv_name = [f'conv{i}_1', f'conv{i}_2']
           for i_kernel, i_pad, i_conv in zip(kernel_size_, padding_,
                                              conv_name):
               self.add_module(
                   i_conv,
                   nn.Conv2d(
                       channels,
                       channels,
                       tuple(i_kernel),
                       padding=i_pad,
                       groups=channels))
       self.conv3 = nn.Conv2d(channels, channels, 1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

task与yaml配置

详见：https://blog.csdn.net/shangyanaf/article/details/136057088