- 1技术实践|使用 Agents for Amazon Bedrock 构建智能体和知识库 - 金蝶发票云票据助手的开发实践...
- 2oracle对象授权中的方案添加,Oracle 中创建方案scheme
- 3最长子序列总结_最长子序列有多少种形态
- 4SAP所有模块用户出口 _sap a004bapi
- 5LLM和数据分析的结合应用_基于llm做数据分析
- 6宝塔面板一键部署SSL证书,免费配置https_宝塔免费证书
- 7matlab 多元多项式回归_Matlab:符号变量、符号函数、泰勒级数
- 8计算机出现找不到msvcp140.dll无法继续执行代码怎么办?推荐7个有效解决方法
- 9AI跟踪报道第49期-新加坡内哥谈技术-本周AI新闻: 开源AI王者归来的一周
- 10k-近邻算法及识别手写数字的案例
BFS:FloodFill算法_flood fill 算法
赞
踩

FloodFill算法简介
Flood Fill算法是一种用于确定与某个给定节点相连的区域的算法,常用于计算机图形学和图像处理。该算法可以用于诸如填充多边形、检测连通区域等任务。Flood Fill算法有多种实现方式,其中最常见的是递归方法和使用栈或队列的迭代方法。
基本思想
Flood Fill算法从一个初始像素开始,检查该像素的颜色。如果颜色匹配(即需要填充的颜色),则将其填充为新的颜色,然后对相邻的像素重复这一过程,直到所有相连的匹配像素都被填充为止。

FloodFill算法也叫洪水灌溉法,上图中0表示岛屿,1表示海洋,如果要我们求岛屿的个数的话就可以用洪水灌溉法则。

灌溉之后就像上面一样。
接下来,我们来练习几道题熟悉一下FloodFill算法。
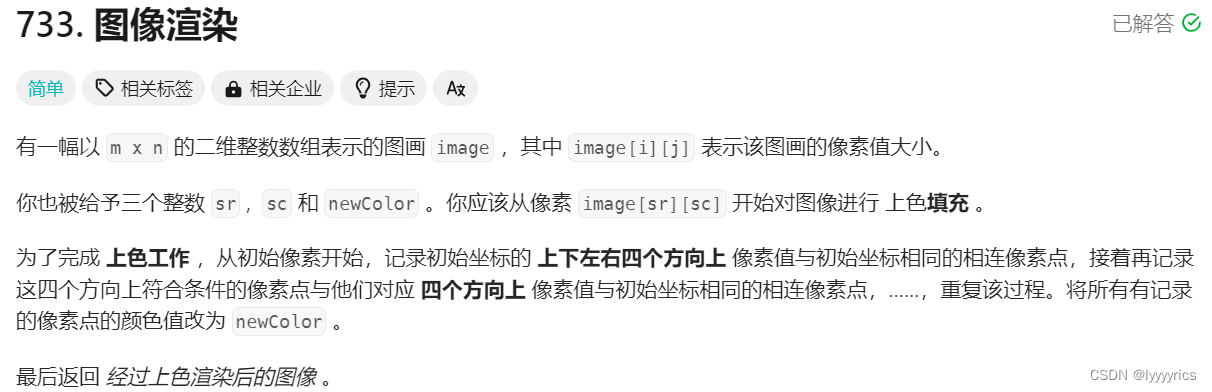
1.图像渲染
题目链接
题目:
样例输入和输出:
这道题的意思很简单,就是我们固定一个位置,这个位置的坐标是[sr,sc]这个位置周围的和这个这个区块数字相同数都会被变成新的数字。
以上面这个例子为例,初始坐标是中间坐标,那么渲染的区块就是:


如果利用FloodFill算法的话,我们按顺序灌溉应该是1->2->3->4。
算法原理:
利用BFS的FloodFill算法,这个算法我们只需要借助队列,每次入队列的时候改变当前节点的值。
代码展示:
class Solution { public: typedef pair<int,long> PIL; //定义一个方向数组,上下左右四个位置 int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) { //标记一下需要修改的像素值 int prev=image[sr][sc]; int m=image.size(); int n=image[0].size(); if(prev==color) { return image;//处理边界情况 } queue<PIL> q; q.push({sr,sc}); while(q.size()) { auto [a,b]=q.front(); q.pop(); image[a][b]=color; for(int i=0;i<4;i++) { int x=a+dx[i]; int y=b+dy[i]; if(x>=0&&x<m&&y>=0&&y<n&&image[x][y]==prev) { q.push({x,y}); } } } return image; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
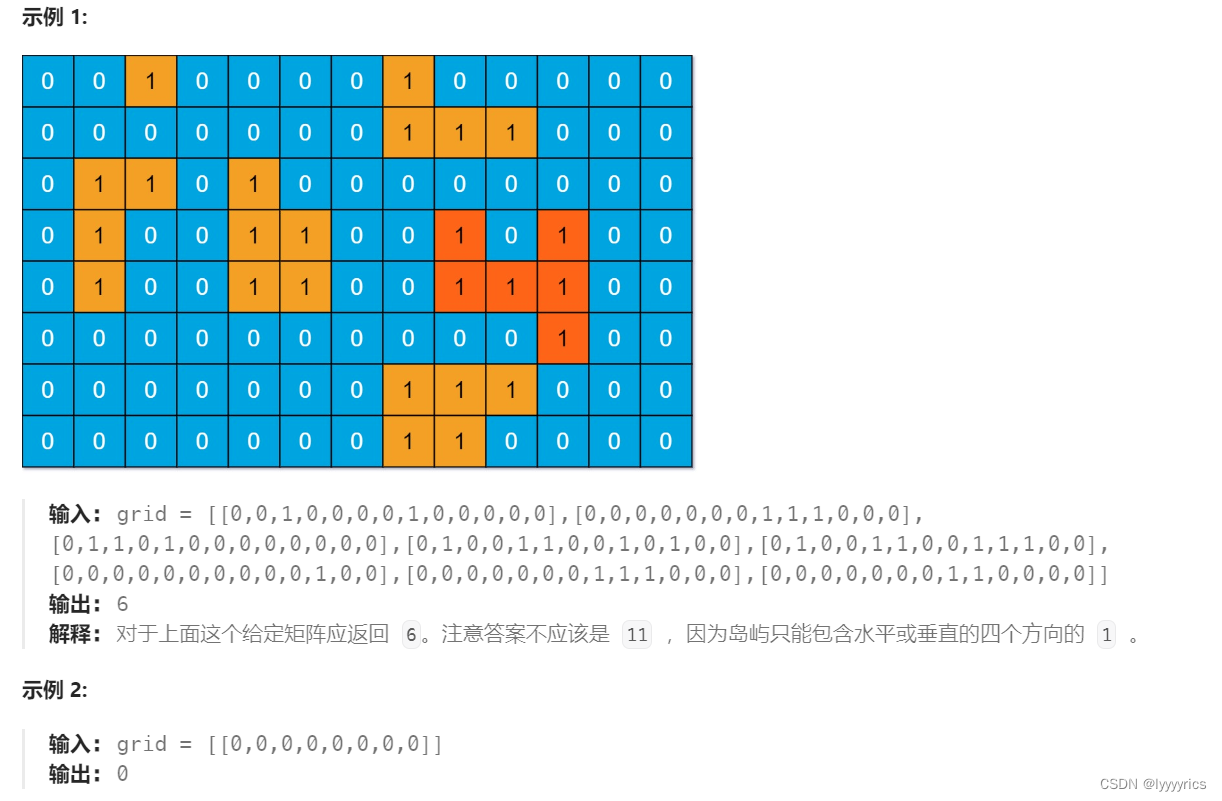
2.岛屿数量
题目链接
题目:
样例输入和输出:
我们来看示例1:
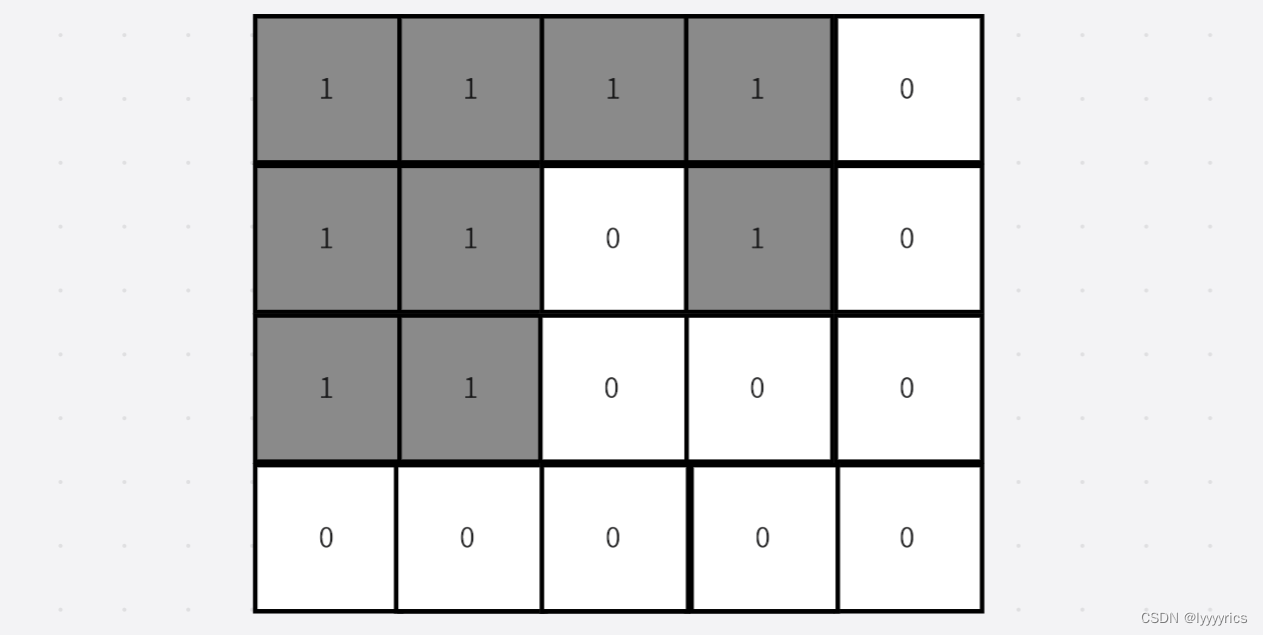
这道题1是岛屿,0是海,然后这个数组的周围默认都是海。
算法原理:
这道题和上道题的思路是一样的,但是还多出来一步,就是当我们利用bfs来遍历数组的时候,假如我们从第一个位置开始遍历,遍历了一遍,记录了一个岛屿,但是我们第二次遍历的时候从第二个位置的1开始遍历,但是第二个位置的1是属于第一个岛屿的,所以这里就会产生重复,解决这种重复问题的办法就是开一个bool类型的vis数组,这个数组的大小和给定的数组的大小是相同的,我们每访问一个岛屿就将这个岛屿上对应的vis变为true,表示我们已经访问过这个节点了,所以这里进行bfs的条件多了一个不仅需要这个节点的值是1,还需要这个节点对应的vis数组是true。
代码展示:
class Solution { public: typedef pair<int,int> PIL; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; bool vis[301][301]; int ret=0; int m,n; void bfs(vector<vector<char>>& grid,int i,int j) { queue<PIL> q; q.push({i,j}); vis[i][j]=false; while(q.size()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;k++) { int x=a+dx[k]; int y=b+dy[k]; if(x < m && x >= 0 && y >= 0&&y<n&&grid[x][y]=='1'&&vis[x][y]==false) { vis[x][y]=true; q.push({x,y}); } } } } int numIslands(vector<vector<char>>& grid) { m=grid.size(); n=grid[0].size(); for(int i=0;i<grid.size();i++) { for(int j=0;j<grid[i].size();j++) { if(grid[i][j]=='1'&&vis[i][j]==false) { bfs(grid,i,j);//将这个陆地标记一下 ret++; } } } return ret; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
3.岛屿的最大面积
题目链接
题目:
样例输入和输出:
这道题的背景和上一道题是一样的,但是这道题不是让我们求岛屿的数量而是让我们求所有岛屿中面积最大的那个岛屿大面积
算法原理:
这道题需要的变量和上道题也是一样的,但是唯一不同的一点是上一道题是void,这道题是int,所以我们需要记录每次BFS的结果,我们用S记录每次BFS的结果,然后每次BFS之后,和前一次求出来的面积进行比较,最后直接返回最大值。
代码展示:
class Solution { public: typedef pair<int,int> PIL; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; bool vis[51][51]; int m,n; int S; int bfs(vector<vector<int>>& grid,int i,int j) { int Sum=0; queue<PIL> q; q.push({i,j}); Sum++; vis[i][j]=true; while(q.size()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;k++) { int x=a+dx[k]; int y=b+dy[k]; if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&vis[x][y]==false) { vis[x][y]=true; q.push({x,y}); Sum++; } } } return Sum; } int maxAreaOfIsland(vector<vector<int>>& grid) { m=grid.size(); n=grid[0].size(); for(int i=0;i<m;i++) { for(int j=0;j<n;j++) { if(grid[i][j]==1&&vis[i][j]==false) { int S1=bfs(grid,i,j); if(S<S1) { S=S1; } } } } return S; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
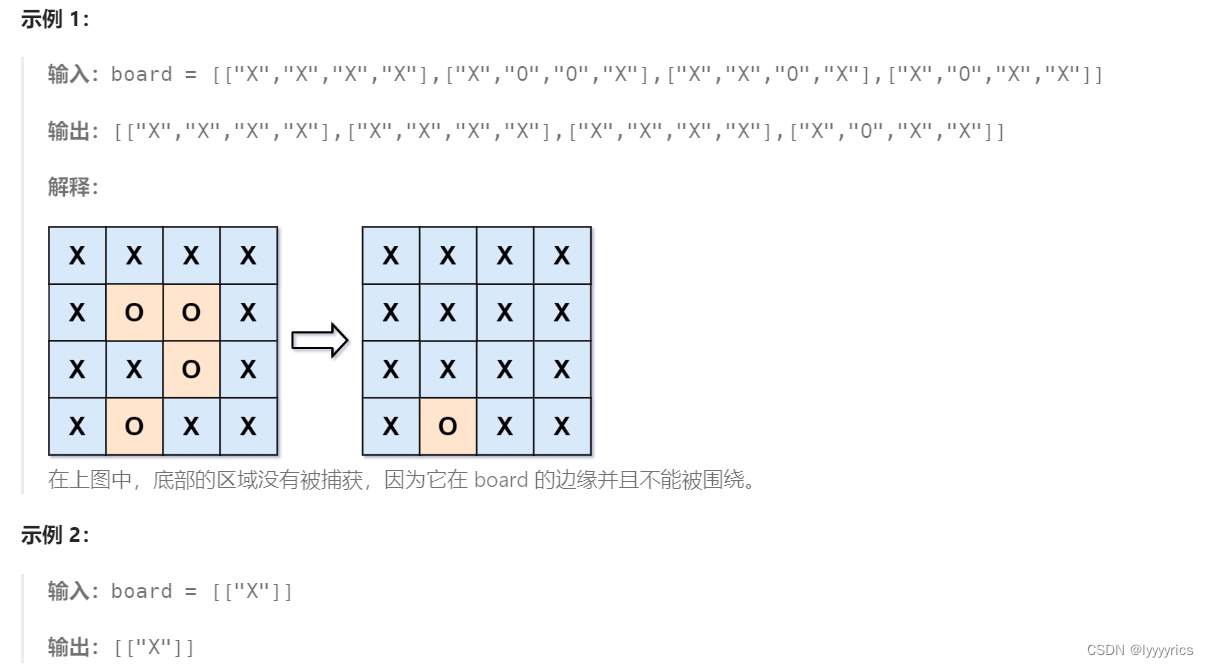
4.被围绕的区域
题目链接
题目:
样例输入和输出:
这道题给出的二维数组中的值只有X和O,这道题的意思就是让我们修改被x包围的O为x,然后边界的联通区域不需要修改。
我们用一个例子来表示上面的题意:
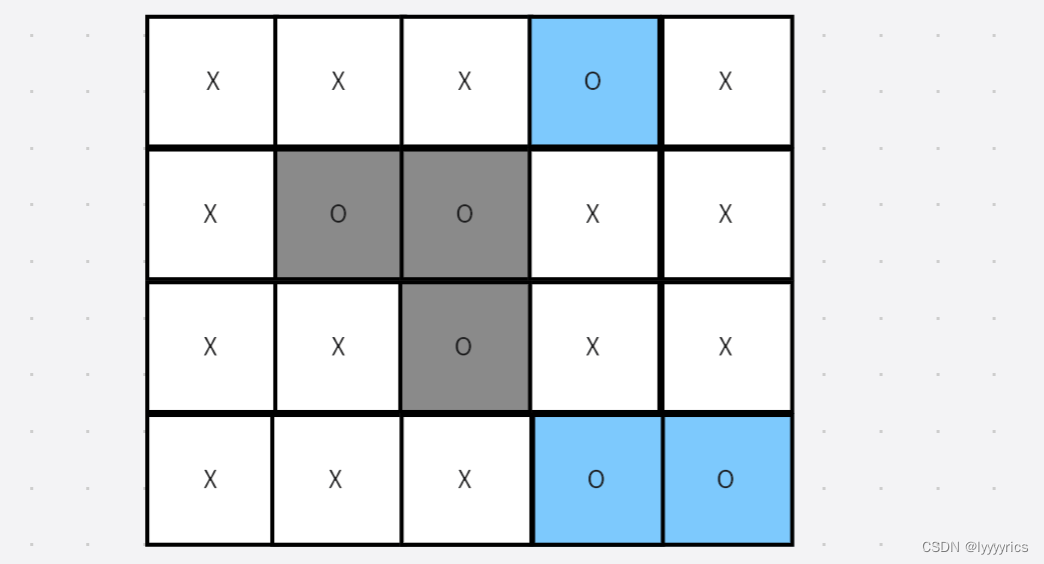
蓝色区域表示不能修改的边界联通区域,灰色区域表示被X围住的中间的需要修改的联通区域。
算法原理,如果这道题我们直接正面做的话,很难,因为当我们进行BFS的时候,我们并不知道这块区域是边界联通的区域,就像下面这种情况:
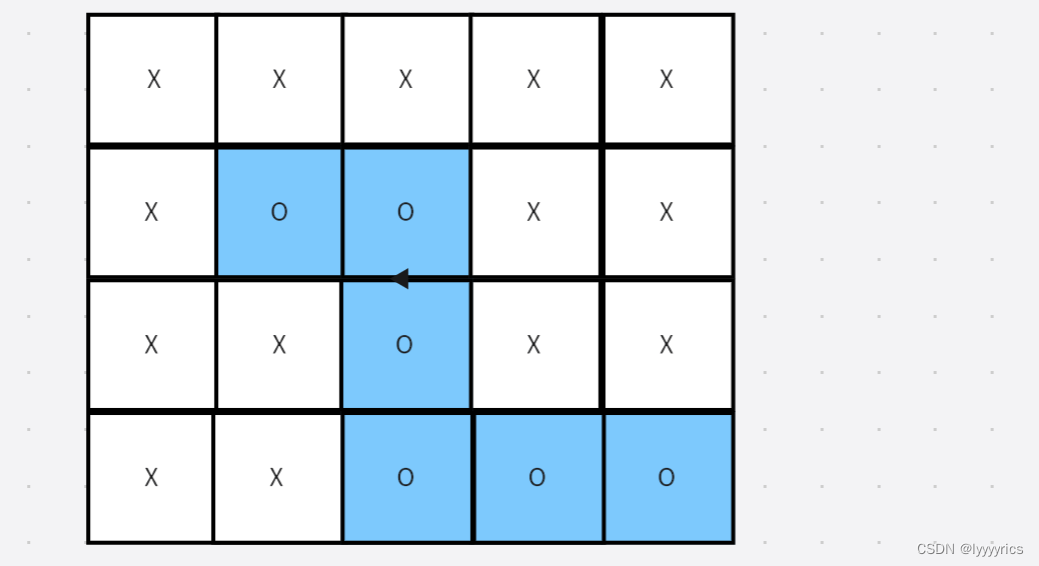
上面这种情况,当我们从第一个位置开始BFS我们到后面才知道这个联通区域是边界区域,但是我们又不能倒过去找,所以我们只能先标记这个边界区域,然后再用一次BFS对可修改区域进行修改,所以这里我们先对边界区域进行遍历,先把边界区域修改为另一个字符,这里我们将这个字符定义为’*'修改了之后,我们只需要对这个二维数组遍历一遍,将O修改为X,将 *修改为O即可。
代码展示:
class Solution { public: typedef pair<int,int> PII; int m,n; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; void bfs(vector<vector<char>>& board,int i,int j) { queue<PII> q; q.push({i,j}); board[i][j]='*'; while(q.size()) { auto [a,b]=q.front(); q.pop(); for(int k=0;k<4;k++) { int x=a+dx[k]; int y=b+dy[k]; if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='O') { q.push({x,y}); board[x][y]='*'; } } } } void solve(vector<vector<char>>& board) { m=board.size(); n=board[0].size(); for(int j=0;j<n;j++) { if(board[0][j]=='O')bfs(board,0,j); if(board[m-1][j]=='O')bfs(board,m-1,j); } for(int i=0;i<m;i++) { if(board[i][0]=='O')bfs(board,i,0); if(board[i][n-1]=='O')bfs(board,i,n-1); } for(int i=0;i<m;i++) { for(int j=0;j<n;j++) { if(board[i][j]=='O') board[i][j]='X'; if(board[i][j]=='*') board[i][j]='O'; } } } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
总结
Flood Fill算法在图像处理和计算机图形学中扮演着重要角色。无论是用于简单的填色任务,还是复杂的区域检测,这一算法都展示了其强大的功能。本文详细介绍了Flood Fill算法的基本思想,并提供了递归和迭代两种实现方式。递归方法虽然简单直观,但在处理较大图像时可能会遇到递归深度的限制;而迭代方法则通过显式管理待填充的像素,克服了这一问题。
通过这两种实现方法的比较,我们不仅了解了Flood Fill算法的原理,也掌握了如何选择合适的实现方式来应对不同的应用场景。希望这篇博客能帮助大家更好地理解和应用Flood Fill算法,在实际项目中解决相关问题。
如果您有任何问题或需要进一步讨论,欢迎在评论区留言。感谢您的阅读!