金融风控实战——可解释人工智能技术_可解释性人工智能

可解释的基本概念

机器学习/人工智能可解释性（简称 XAI）正变得越来越流行。随着算法在金融、医疗保健和保险等行业的高风险决策中变得越来越普遍，对可解释性的需求持续增长。关于“可解释性”的精确定义，目前工业界和学术界仍未达成一个统一的标准，但是一个比较简单直接的定义为：“可解释性”是帮助 人工智能技术的的决策和行为能够被人类理解的一系列方法。

可解释人工智能技术中的大部分概念和我们熟悉的人工智能技术中的概念是完全相同的，例如数据集，样本，特征，模型等等，这里需要额外说明两个在可解释人工智能技术中相对比较独特的两个概念。

黑盒模型，灰盒模型和白盒模型

黑盒模型是⼀个内部机制无法使用人类语言来描述的模型系统。在人工智能技术中，黑盒模型指即使算法工程师通过查看参数也⽆法理解的模型。这其中最典型的就是神经网络模型，大部分神经网络模型都是难以直接使用人类语言逻辑来描述的

灰盒模型相对于黑盒模型而言，经过深入复杂的分析是具备了一定程度上的人类可理解性的，这方面的典型代表就是随机森林，对于随机森林而言，每一棵树对应的分裂规则都是可理解的，而模型最终的决策是完全受每一棵树的判定结果最终进行平均而得到的，因此，一定程度上，我们可以将随机森林的预测解释为大量明确的复合的规则的综合判定。（if else规则）

白盒模型是可以直接使用人类逻辑理解并使用语言表述的模型，这类模型一般都较为简单，例如常见的逻辑回归或单棵决策树，都是可以直接使用人类语言来解释为什么模型会做出这样的预测。典型的例子就是银行使用的基于逻辑回归的传统评分卡

为什么我们需要可解释

1.人类需要不断的持续学习的渴求：
我们逢年过节回家，经常会听到长辈提到自己的“成功”史，因为我当初做了XXXX，所以后来就成为了XXX，赚到了XXX。。。人类在地球上生存了上千年的历史长河里，已经习惯了大量的学习和总结，并产生新的经验和规则等等，因此我们需要模型预测的同时能够提供可解释性以帮助我们更好的理解问题；

2.人类对于未知的探索欲望：例如在信贷申请中，一个用户如果被机器学习模型拒绝了贷款申请，那么对于用户而言，就会非常想知道为什么自己会被拒绝申请，怎么做才能避免自己被拒绝。搞笑的是，这一点也正是欺诈分子所致力于解决的问题，当一个欺诈分子使用的虚拟账号的申请被拒绝的时候，他就会非常想知道怎么去解释模型到底是因为什么而拒绝了虚假账户的贷款，是账户的邮箱使用了临时邮箱？还是虚拟账号和其它高危账号存在关联？另⼀个例⼦是令人讨厌的广澳推荐，就我个⼈⽽⾔，我⼀直都很疑惑为什么知乎总是给我推荐相亲广告，是因为我的年龄正好到了适婚年龄？还是因为我经常浏览关于婚恋相关的问题又或者是因为我的职业是一名程序员？

3.我们希望模型能够教会我们新的知识：在许多科学学科中，从定性⽅法到定量⽅法 (例如社会学、⼼理学)，以及到机器学习 (⽣物学、基因组学) 都发⽣了变化。科学的目标是获取知识，但是许多问题都是通过⼤数据集和⿊盒机器学习模型来解决的。模型本⾝应该成为知识的来源。可解释性使得人类可以提取模型捕获的这些额外知识；

4.我们需要使用人类的经验和知识来辅助模型：这一点在小样本问题中是比较重要的，模型只是没有感情的代码，由一大堆参数构成，模型只能模型和近似人类逻辑，在小样本问题中，模型很容易近似错误的逻辑，例如对于一个小型的信贷评分卡项目，如果正负样本恰好分别是北京人和上海人，则模型很容易学习到上海人都是好客户而北京人都是坏客户这样错误的知识；

5.我们需要通过对模型的解释来让人们更容易信任模型：对于一些重要的决策，例如电商领域中对销量的预测结果如果作为补货的重要依据，则我们希望模型能够具备很严谨的可解释逻辑，因为一旦模型出错则可能会带来很大的损失；

6.处理法律法规和政策风险：在消费行业，用户的订单如果因为模型的判断而被取消，用户是可以投诉消费者协会的，则决策者往往需要对用户和相关政府机构提供充足的证据证明这笔订单被取消的原因。同样，在金融领域也存在类似的问题；

7.提高模型的鲁棒性：这一点和第四点类似，通过对模型进行解释，我们可以知道模型为什么会做出这样的决策，很多时候，由于训练数据的大小或者有偏等问题，模型很容易学习到一些错误的知识，例如我们的训练数据集中，欺诈用户的性别全是女性，正常用户的性别全是男性，则模型很容易误认为女性=欺诈用户，因此一旦欺诈用户更改性别的设置，很容易使得模型的预测结果发生巨大的变化，即模型的鲁棒性很差；

8.可解释性可以帮助算法工程师更好的调试模型：这一点相信大家应该是最熟悉的，对于常用的xgboost模型，我们常常会根据tree的特征重要性，去对高特征重要性的特征进行一些组合特征的衍生，从而进一步提高模型的增益，可解释性可以更好的帮助我们理解模型，分析模型为什么会对样本发生误判等；

什么时候我们不需要考虑可解释性

总体而言，不会造成重大影响的应用或者可解释性会产生危害的应用不需要考虑可解释性

对于推荐系统而言，其对可解释性的需求就不高，因此推荐中一大堆复杂的深度学习模型，主要而言，模型对于用户的商品推荐并不会产生重要的影响，即使推荐错误，最大的代价也就是用户不点击商品，电商平台少一些利润而已；或企业内部的预警系统，对于产生的异常，人工去查证从而降低监控的成本等；

在反欺诈领域的一些应用里，例如流量反欺诈，本身是用户无感的，并且对于虚假流量的检测和剔除本身也不会造成影响，这个时候，如果使用可解释性去解释模型的检测机制是存在风险的，因为欺诈用户很容易通过可理解的逻辑去改变自己的欺诈策略，从而轻松绕过现有的反欺诈模型体系

可解释方法的分类

根据可解释方法的在模型中的应用过程

1.在模型训练时的可解释方法：例如我们通过对逻辑回归设定l1正则化从而尽量让无用的特征权重系数为0，从而使得逻辑回归的权重系数更稀疏，从而更好理解不同的特征对预测结果的贡献；或我们通过设置单个决策树的深度，使得决策树能够更好理解；

2.在模型训练之后的可解释方法：在模型训练之后的可解释方法基本上都是模型无关的，即这种方法可以适用于广泛的任意的模型，例如permutation importance，通过对特征进行shuffle然后比较验证集的预测结果从而特征是否为噪声特征；

根据可解释方法的输出

1.输出统计指标：例如gbdt中的特征重要性，为每个特征返回一个特征重要性值，从而描述特征在训练过程中对目标任务的贡献程度；
2.输出可视化结果：特征的部分依赖图就是这样⼀种情况。部分依赖图是显⽰特征随着取值变化之后，模型预测结果的变化曲线。呈现部分依赖关系的最佳⽅法是实际绘制曲线，⽽不是打印坐标；
3.模型本身容易解释：上文题都的白盒模型；
4.输出样本：这个类别的⽅法是返回样本以使模型可解释。这种方法在nlp和cv中特别有用，例如下图：

是否特定于模型

特定于模型的解释⽅法仅限于特定的模型类，例如线性模型中回归权重的解释就是特定于模型的解释，因为根据定义，本质上可解释模型的解释通常是特定于模型的解释。

相对应的，与模型⽆关的⼯具可以⽤于任何机器学习模型，并在模型经过训练后应⽤ (事后的)。这些模型⽆关的⽅法通常通过分析特征输⼊和输出来⼯作。根据定义，这些⽅法是不能访问模型的内部信息，如权重或结构信息。

基于局部还是全局

解释⽅法是否解释单个实例预测或整个模型⾏为？还是范围介于两者之间？

个人总结

从应用层面来看，一般来说，我们将可解释性方法划分为四类：
1.从样本层面出发，对样本进行一些特定分析和处理从而解释模型；
2.从特征层面出发，对特征进行一些特定分析和处理从而解释模型；
3.从模型层面出发，对模型进行一些特定分析和处理从而解释模型；
4.从代理模型层面出发，使用简单的可解释模型作为复杂的黑盒模型的代理近似，从而间接解释黑盒模型；
5.混合

后面我们会对这几种方法展现一些具体的案例，我们先来看看最常见的，从模型层面出发的可解释方法

工具函数定义

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
def plot_feature_importance(importances,feature_names):
    feature_importance=pd.DataFrame()
    feature_importance['features']=feature_names
    feature_importance['importance']=importances
    feature_importance.sort_values(by='importance', ascending=False,inplace=True)
    plt.figure(figsize=(16, 16))
    fig=sns.barplot(data=feature_importance, \
                    x='importance', y='features').set(xlim=(min(importances),max(importances)));
    return feature_importance.reset_index(drop=True)
    
def plot_effect(importances,feature_names,features):
    feature_importance=pd.DataFrame()
    for i,col in enumerate(feature_names):
        feature_importance[col]=features[col]*importances[i]
    for col in feature_importance.columns:
        plt.figure(figsize=(4,4))
        feature_importance[col].plot(kind='box')
    feature_importance.sort_values(by='importance', ascending=False,inplace=True)
    return feature_importance.reset_index(drop=True)


def plot_sample_effect(importances,feature_names,features):
    sample_importance=pd.DataFrame()
    sample_importance['feature']=feature_names
    res=[]
    for i,col in enumerate(feature_names):
        res.append(importances[i]*features[i])
    sample_importance['importance']=res
    sample_importance.sort_values(by='importance', ascending=False,inplace=True)
    
    plt.figure(figsize=(16, 16))
    fig=sns.barplot(data=sample_importance, \
                    x='importance', y='feature')
    return sample_importance.reset_index(drop=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

模型层面的可解释

逻辑回归的例子

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score
df = pd.read_csv(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data",
    header=None)
df.columns = [
    "Age", "WorkClass", "fnlwgt", "Education", "EducationNum",
    "MaritalStatus", "Occupation", "Relationship", "Race", "Gender",
    "CapitalGain", "CapitalLoss", "HoursPerWeek", "NativeCountry", "Income"
]
train_cols = df.columns[0:-1]
label = df.columns[-1]
X = pd.get_dummies(df[train_cols])
y = df[label]
y=y.factorize()[0]     #y>50或者<=50
X_train,X_test,y_train,y_test=train_test_split(X,y,stratify=y,test_size=0.2)
#stratify是为了保持split前类的分布。比如有100个数据，80个属于A类，20个属于B类。如果#train_test_split(... test_size=0.25, stratify = y_all), 那么split之后数据如下： 
#training: 75个数据，其中60个属于A类，15个属于B类。 
#testing: 25个数据，其中20个属于A类，5个属于B类。 

from sklearn.linear_model import LogisticRegression
lr= LogisticRegression()
lr.fit(X_train,y_train)
roc_auc_score(y_test,lr.predict_proba(X_test)[:,1])
#0.5915883390767834
plot_feature_importance(lr.coef_.tolist()[0],list(X_train.columns))
或者
'''pd.DataFrame({"features":X_train.columns,"importance":lr.coef_.tolist()[0]}).sort_values("importance",ascending=False)'''
'''
a = pd.Series(lr.coef_.tolist()[0],index=X_train.columns)
plt.figure(figsize=(20,10))
a.sort_values(ascending=False).plot(kind="bar")
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

可以看到，我们通过可视化逻辑回归的权重系数结合逻辑回归本身的决策逻辑，很容易理解逻辑回归的整个决策过程，除此之外，更重要的是，我们可以看到，对于上述逻辑回归模型，其稳定性是较差的，可以看到，模型受到部分很少量特征的影响非常大，则模型很容易失效（（例如欺诈分子可以修改通过修改年龄轻易修改绕开模型检测）），我们最为理想的情况应该是所有的权重系数尽量均匀，这样模型的鲁棒性会比较强。

这个时候，我们先去看看数据的情况，数据没有进行标准化则很容易出现这种问题

可以看到，原始的特征没有进行标准化处理，所以逻辑回归模型的权重在会在大量纲的特征上变得很大，这是由于梯度下降法优化而导致的（逻辑回归、线性回归、神经网络这类以梯度下降法求参数的模型容易受到特征量纲的影响）

X_train
1

X_test
1

from sklearn.preprocessing import MinMaxScaler
mms=MinMaxScaler()
cols=list(X_train.columns)

mms.fit(X_train[cols])

X_train[cols]=mms.transform(X_train[cols])
X_test[cols]=mms.transform(X_test[cols])

X_train
1
2
3
4
5
6
7
8
9
10

X_test
1

lr= LogisticRegression()
lr.fit(X_train,y_train)
plot_feature_importance(lr.coef_.tolist()[0],list(X_train.columns))
1
2
3

roc_auc_score(y_test,lr.predict_proba(X_test)[:,1])
#0.9129606797218381
1
2

可以看到，通过模型本身的可解释性质，我们从特征重要性上，发现数据标准化的问题没有处理，从而对数据进行标准化，提高了模型的鲁棒性，可以看到，特征的重要程度相对来说更加均衡。同时我们可以看到capital gain的重要性非常高超过了16，对于一个理想的逻辑回归而言，我们希望模型的权重系数尽量保持在一个较小的范围内，否则大权重对应的特征一旦发生微小的变化很容易使得预测结果发生巨大的变化从而降低了模型的鲁棒性，我们通过l2正则化对齐进行约束即可

lr= LogisticRegression(C=0.01)
lr.fit(X_train,y_train)
plot_feature_importance(lr.coef_.tolist()[0],list(X_train.columns))
1
2
3

roc_auc_score(y_test,lr.predict_proba(X_test)[:,1])
#0.8896387043189369
1
2

通过上述的整个过程，我们就完成了一个基本的模型可解释的应用，通过模型本身的可解释性我们优化了模型的表现，同时作为白盒模型的逻辑回归模型可以直接使用人类语言来描述模型的预测过程。

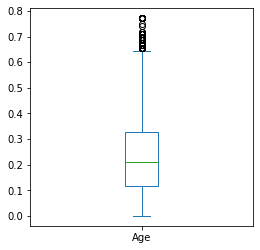
下面，我们在此基础上，引入特征层面的可解释方法，对于逻辑回归而言，我们需要计算逻辑回归的权重为每一个特征带来的计算结果的区间，我们一般称之为effect plot

以age对应的图为例，我们可以看到，对于大多数样本而言，age为样本所提供的预测的贡献在0.1到0.3之间，而少部分年龄较大的用户其提供的预测则较高超过了0.6,更详细的报告可以看下表，可以看到，Age这个特征对于大部分用户提供的预测为1的平均贡献约为0.21左右(标准化以后了)

def plot_effect(importances,feature_names,features):
    feature_importance=pd.DataFrame()
    for i,col in enumerate(feature_names):
        feature_importance[col]=features[col]*importances[i]
    for col in feature_importance.columns:
        plt.figure(figsize=(4,4))
        feature_importance[col].plot(kind='box')
    return feature_importance.reset_index(drop=True)
    
feature_importance= plot_effect(lr.coef_.tolist()[0],X_train.columns,X_train)
1
2
3
4
5
6
7
8
9
10

feature_importance.describe()
1

最后，我们从样本层面出发来进行可解释

对于逻辑回归而言，单个样本的可解释和上述的过程是类似的，假设我们想要知道模型为什么倾向于将某个样本预测为1或预测为0，则我们可以这么做

def plot_sample_effect(importances,feature_names,features):
    sample_importance=pd.DataFrame()
    sample_importance['feature']=feature_names
    res=[]
    for i,col in enumerate(feature_names):
        res.append(importances[i]*features[i])
    sample_importance['importance']=res
    sample_importance.sort_values(by='importance', ascending=False,inplace=True)
    plt.figure(figsize=(16, 16))
    fig=sns.barplot(data=sample_importance, x='importance', y='feature')
    return sample_importance.reset_index(drop=True)

sample_importance=plot_sample_effect(lr.coef_.tolist()[0],list(X_train.columns),X_train.iloc[0].tolist())
1
2
3
4
5
6
7
8
9
10
11
12
13

可以看到，单个样本的局部特征重要性结果和全局的特征重要性结果存在巨大的差异，全局特征重要性从整体上考虑特征的贡献情况，优点在于可以快速的从整体上理解模型的解释性，缺点在于我们无法知道每个样本的预测差异，核心原因在于，每个样本的特征都是不同的，因此最终模型作用于每个样本的效果也是存在很大区别的。

从样本层面的可解释可以直接作为bad case分析的重要依据（预测不准）（正负样本概率分布图结果存在交叉部分），例如，我们假设上述的这个样本是预测错误的样本，则我们可以看到模型对样本实际的预测过程中，martialstatus这个特征对于样本预测为1的贡献是最大的，因此我们可以优先从这个角度出发看看能够对这类特征进行一些变换或衍生从而缓解误判的问题

上述过程，我们也可以使用interpret这个开源工具来帮助实现

from interpret import set_visualize_provider
from interpret.provider import InlineProvider
set_visualize_provider(InlineProvider())

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

from interpret.glassbox import LogisticRegression
from interpret import show


lr = LogisticRegression(random_state=seed,fit_intercept=False)
lr.fit(X_train, y_train)

lr_global = lr.explain_global()
show(lr_global)

lr_local = lr.explain_local(X_test[:5], y_test[:5])
show(lr_local)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

但是对于定制化的需求，interpret支持的并不是很好，索性这些逻辑也都不复杂，问题不大，可以自己手撸

决策树的例子

对于决策树而言，其基于模型的可解释方法和逻辑回归存在很大不同，对于tree模型而言，我们就不需要做标准化处理了

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score
df = pd.read_csv(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data",
    header=None)
df.columns = [
    "Age", "WorkClass", "fnlwgt", "Education", "EducationNum",
    "MaritalStatus", "Occupation", "Relationship", "Race", "Gender",
    "CapitalGain", "CapitalLoss", "HoursPerWeek", "NativeCountry", "Income"
]
train_cols = df.columns[0:-1]
label = df.columns[-1]
X = pd.get_dummies(df[train_cols])
y = df[label]
y=y.factorize()[0]
X_train,X_test,y_train,y_test=train_test_split(X,y,stratify=y,test_size=0.2)

from interpret import set_visualize_provider
from interpret.provider import InlineProvider
set_visualize_provider(InlineProvider())

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

from interpret.glassbox import ClassificationTree
from interpret import show


dt = ClassificationTree(random_state=seed)
dt.fit(X_train, y_train)

dt_global = dt.explain_global()
show(dt_global)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

dt_local = dt.explain_local(X_train[:5], y_train[:5])
show(dt_local)
1
2

对于tree而言，由于其训练过程中的特征用于分裂，因此不像线性模型那样存在乘的关系，所以我们只能通过其特征重要性来对特征层面的可解释进行实现，而对于每个样本层面上的特征贡献，我们通过上图的决策路径来理解模型决策的过程就可以了

plot_feature_importance(dt.sk_model_.feature_importances_.tolist(),list(X_train.columns))
1

roc_auc_score(y_test,dt.predict_proba(X_test)[:,1])
#0.8507308067311858
1
2

skope rules的例子

skope rules是一种特殊的随机森林，原理并不复杂，其实就是通过行列采样构建出了大量的tree，然后对其中每个tree的性能进行评估，将其中性能最好的部分tree输出成为规则集合，在可解释性和性能之间进行了一定的折衷

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

from interpret.glassbox import DecisionListClassifier
from interpret import show

dl.sk_model_
#SkopeRules(feature_names=['feature_0', 'feature_1', 'feature_2', 'feature_3',
#                          'feature_4', 'feature_5', 'feature_6', 'feature_7',
#                          'feature_8', 'feature_9', 'feature_10', 'feature_11',
#                          'feature_12', 'feature_13', 'feature_14',
#                          'feature_15', 'feature_16', 'feature_17',
#                          'feature_18', 'feature_19', 'feature_20',
#                          'feature_21', 'feature_22', 'feature_23',
#                          'feature_24', 'feature_25', 'feature_26',
#                          'feature_27', 'feature_28', 'feature_29', ...],
#           random_state=1)
dl = DecisionListClassifier(random_state=seed,n_estimators=10, \
                            max_samples=0.8, max_samples_features=0.8, \
                            max_depth=10,precision_min=0.55,
                 recall_min=0.55)
dl.fit(X_train, y_train)
dl_global = dl.explain_global()
show(dl_global)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

dl_local = dl.explain_local(X_test[:15], y_test[:15])
show(dl_local)
1
2

对于金融风控中简单的规则挖掘而言，skope rules是一个比较方便强大的工具，可以快速生成大量规则

特征层面的可解释

从上述的过程中，我们可以看到，模型层面的可解释方法是非常局限的，并且特定于模型，对于我们常用的xgboost，lightgbm，catboost等，模型层面的可解释方法并不足够，并且也并不好理解，对于单个决策树而言，我们可以很清晰的观察其决策路径，但是对于gbdt而言，往往包含了成百上千的tree，即使可视化了所有树的决策路径，对于人类而言也是非常难理解的，下面我们来看一下对于复杂的模型而言，从特征层面出发有哪些可解释的方法

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score
df = pd.read_csv(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data",
    header=None)
df.columns = [
    "Age", "WorkClass", "fnlwgt", "Education", "EducationNum",
    "MaritalStatus", "Occupation", "Relationship", "Race", "Gender",
    "CapitalGain", "CapitalLoss", "HoursPerWeek", "NativeCountry", "Income"
]
train_cols = df.columns[0:-1]
label = df.columns[-1]
X = pd.get_dummies(df[train_cols])
y = df[label]
y=y.factorize()[0]
X_train,X_test,y_train,y_test=train_test_split(X,y,stratify=y,test_size=0.2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

import xgboost as xgb
clf=xgb.XGBClassifier(n_estimators=50)
clf.fit(X_train,y_train)
#XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
#              colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,
#              importance_type='gain', interaction_constraints='',
#              learning_rate=0.300000012, max_delta_step=0, max_depth=6,
#              min_child_weight=1, missing=nan, monotone_constraints='()',
#              n_estimators=50, n_jobs=12, num_parallel_tree=1, random_state=0,
#              reg_alpha=0, reg_lambda=1, scale_pos_weight=1, subsample=1,
#              tree_method='exact', validate_parameters=1, verbosity=None)
roc_auc_score(y_test,clf.predict_proba(X_test)[:,1])
#0.9315672009450899
plot_feature_importance(clf.feature_importances_.tolist(),list(X_train.columns))
1
2
3
4
5
6
7
8
9
10
11
12
13
14

通过可视化树的特征重要性是最为简单直接的特征层面的可解释方法，除此之外，后续又衍生出了许多类似于feature importance的特征可解释方法例如permutation importance和null importance以及lofo importance，rfe等等。可以看到，gbdt的这种可解释性方法非常的粗糙，因为仅能从一个比较大的level来解释特征的效果，但是实际上我们其实无法用语言来进一步描述模型是怎么工作的，这种层面的可解释大都只能作为模型的调试和优化以及特征选择来使用而无法直接对外输出为人类语言逻辑

而如果要较好的解释xgb这类复杂模型，则我们需要使用到基于特征和基于样本的可解释方法，一般我们也把这两种可解释方法称为模型无关的可解释方法，这也是目前复杂模型的主要的可解释手段

部分依赖图

首先是常用的部分依赖图

from sklearn.inspection import partial_dependence, plot_partial_dependence
list(X.columns)
#['Age',
# 'fnlwgt',
# 'EducationNum',
# 'CapitalGain',
#
# 'NativeCountry_ Thailand',
# 'NativeCountry_ Trinadad&Tobago',
# 'NativeCountry_ United-States',
# 'NativeCountry_ Vietnam',
# 'NativeCountry_ Yugoslavia']
1
2
3
4
5
6
7
8
9
10
11
12

部分依赖图的原理比较简单，对于这里的二分类问题而言，下面的计算过程实际上是，将X_train中所有样本的age依次从小到大设置为原始的age特征中值，例如原始的年龄范围为15~60，则所有样本的age会统一被设置为15，16.。。60，具体的设置的范围根据我们的参数来定义，通过这种方式，我们可以直观的了解，对于模型而言，随着某个特征取值的变化，模型的预测结果发生的变化情况。

可以看到，下图中，随着年龄增加，模型整体的预测概率的均值是逐渐上升的，而后超过50之后又逐渐下降，这样的U型分布和我们平常在风控里对年龄的认知也是相似的

fig, ax = plt.subplots(figsize=(15,15))
ax.set_title("Age")
plots = plot_partial_dependence(clf,       
                                   features=['Age'],
                                   X=X_train,          
                                   grid_resolution=100,kind= 'both',ax=ax) 
1
2
3
4
5
6

fig, ax = plt.subplots(figsize=(15,15))
ax.set_title("EducationNum")
plots = plot_partial_dependence(clf,       
                                   features=['EducationNum'],
                                   X=X_train,          
                                   grid_resolution=100,kind= 'both',ax=ax) 
1
2
3
4
5
6

fig, ax = plt.subplots(figsize=(15,15))

plots = plot_partial_dependence(clf,       
                                   features=[('Age','EducationNum')],
                                   X=X_train,          
                                   grid_resolution=100,ax=ax) 
1
2
3
4
5
6

当然，如果我们想要看两个以上的交互特征的变化对模型预测结果的影响，思路也是一样的，例如age，educationnum的双特征交互，我们只需要对两个特征的取值进行组合即可，例如age取100个点，educationnum取100个点，则一共是10000个不同的取值组合和10000次的预测，对于海量数据来说，一般我们会对计算次数进行限制避免过多的模型预测过程，因为速度会非常慢

当然，部分依赖图也很容易扩展到样本层面的解释，我们只需要取部分样本进行部分依赖图的绘制就可以了，例如

fig, ax = plt.subplots(figsize=(10,10))
ax.set_title("EducationNum")
plots = plot_partial_dependence(clf,       
                                   features=['EducationNum'],
                                   X=X_train.sample(2),          
                                   grid_resolution=100,kind= 'both',ax=ax) 
1
2
3
4
5
6

我们随机选择2个用户进行pdp的绘制，可以看到，不同用户的Age的取值的变化所造成的模型概率的预测影响差异很大。这种针对样本进行解释的图我们也称之为个体期望图（Ice）

部分依赖图的计算很直观部分依赖图很容易实现。部分依赖图的计算具有因果关系。我们⼲预⼀项特征并测量预测的变化。在此过程中，我们分析了特征与预测之间的因果关系。

但是部分依赖图的缺点也很明显
独立性的假设是 PD 图最⼤的问题。假定针对其计算了部分依赖性的特征与其他特征不相关。例如，假设你要根据⼀个⼈的体重和⾝⾼来预测⼀个⼈⾛多快。对于其中⼀个特征 (例如⾝⾼) 的部分依赖性，我们假设其他特征 (体重) 与⾝⾼不相关，这显然是错误的假设。对于某个⾝⾼ (例如 200 厘⽶) 的 PDP 的计算，我们对体重的边际分布求平均值，其中可能包括 50 公⽄以下的体重，这对于2 ⽶⾼的⼈来说是不现实的。换句话说：当特征关联时，我们会在特征分布区域中创建实际概率⾮常低的新数据点 (例如，某⼈⾝⾼ 2 ⽶但体重不⾜ 50 公⽄的概率不⼤)。解决这个问题的⼀种⽅法是适⽤于条件分布⽽⾮边际分布的累积局部效应图或简称 ALE 图。

异质效应可能被隐藏，因为 PD 曲线仅显⽰平均边际效应。假设对于⼀个特征，你的数据点中的⼀半与预测具有正相关关系——特征值越⼤，预测值越⼤——另⼀半有负相关性——特征值越⼩，预测值越⼤。PD 曲线可能是⼀条⽔平线，因为数据集的两半的效果可能会相互抵消。然后，你可以得出结论，该特征对预测没有影响。通过绘制个体条件期望曲线⽽不是聚合线，我们可以发现异构效应。例如下图

累积局部效应

累积局部效应（ALE）主要用来描述特征与预测值的平均关系，基本上与 PDP 的功能相同，但 ALE 利用了条件分布（ Conditional Distribution）的概念，摆脱了「特征独立的假设」使得结果更于稳健。因此，在应用上 ALE 是比 PDP 更广泛的 。 PDP 与 ALE 的比较如下表所示：

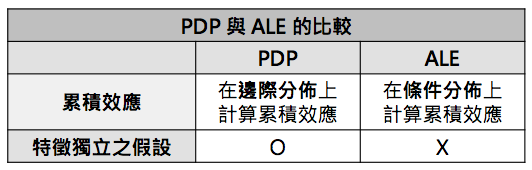
ALE 的分析步骤如下：

• 1.将欲观察的特征x1分为多个区间（区间大小可任意决定）。
• 2.对于每个区间，将区间内的所样本点除了x₁之外的特征值代入，并将x₁以该区间的上下界代入模型，得到两个上下界的预测结果。
• 3.计算每个样本点上下界的预测差异，并对该区间的预测差异值取平均。
• 4.累加前面所有区间的平均预测差异，最后得到每一区间 特征 x₁ 对预测值 y 的平均影响

ALE 图是无偏的，这意味着在特征相关时它们仍然有效。在这种情况下，部分依赖图将失败，因为它们会边缘化不太可能甚⾄物理上不可能的特征值组合。ALE 绘图的计算速度比 PDP 更快

ALE 图的解释很清楚：在给定值的条件下，可以从 ALE 图中读取更改特征对预测的相对影响。

缺陷：
ALE 图可能会变得有些不稳定 (许多⼩起伏)，间隔很多。在这种情况下，减少间隔数可以使估计更稳定，但也可以使预测模型的实际复杂度消除和隐藏。没有完美的解决方案来设置间隔的数量。如果数量太⼩，则 ALE 图可能不太准确。如果数量太⼤，曲线可能会变得不稳定。与 PDP 不同，ALE 图不附带 ICE 曲线。对于 PDP 来说，ICE 曲线是很好的，因为它们可以揭⽰特征效应的异质性，这意味着对于数据⼦集⽽⾔，特征的效应看起来有所不同。对于 ALE 图，你只能检查每个间隔实例之间的效应是否不同，但是每个间隔具有不同的实例，因此它与 ICE 曲线不同。

permutation importance

permutation importance的思路也比较直接，即对特征进行shuffle然后重新预测观察模型的预测结果的变化情况，permutation importance的主要作用是用于检测特征是否为噪声特征，对于噪声特征而言，对其进行shuffle并不会显著影响模型的预测结果变化，对于重要特征而言，shuffle之后模型的预测结果会发生较大变化。

from sklearn.metrics import make_scorer
auc=make_scorer(roc_auc_score)
'''
from sklearn.metrics import SCORERS
SCORERS
'''
from sklearn.inspection import permutation_importance
import numpy as np
result = permutation_importance(clf, X_train, y_train, n_repeats=5,
                                random_state=42,scoring=auc)
result
#{'importances_mean': array([ 5.67829006e-02,  1.20504794e-02,  5.81638354e-02,  6.41669483e-02,
#         2.08584694e-02,  2.55826236e-02,  3.61688959e-05,  3.41881477e-03,
#         2.46421372e-03,  0.00000000e+00,  1.64248562e-03,  2.36678172e-03,
#         1.34460472e-03,  4.39421412e-04,  0.00000000e+00,  0.00000000e+00,
#
#         3.84808935e-05,  0.00000000e+00,  0.00000000e+00,  2.15809815e-04,
#         0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
#         0.00000000e+00,  1.00242506e-03,  2.44176928e-04,  0.00000000e+00]),
# 'importances_std': array([1.16379065e-03, 1.00988664e-03, 2.02336528e-03, 1.89800340e-03,
#        9.49718850e-04, 1.21617228e-03, 3.57773737e-05, 2.82843049e-04,
#        5.83117938e-04, 0.00000000e+00, 3.74688244e-04, 2.33453837e-04,
#        1.82527309e-04, 1.72490128e-04, 0.00000000e+00, 0.00000000e+00,
#
#        3.18826718e-05, 0.00000000e+00, 0.00000000e+00, 5.17407337e-05,
#        0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
#        0.00000000e+00, 4.42826018e-04, 1.05045229e-04, 0.00000000e+00]),
# 'importances': array([[ 5.69991957e-02,  5.83838226e-02,  5.76021692e-02,
#          5.55529155e-02,  5.53763999e-02],
#        [ 1.11620508e-02,  1.31821667e-02,  1.17392642e-02,
#          1.32948645e-02,  1.08740507e-02],
#       
#        [ 8.39929036e-04,  5.46386768e-04,  6.59084556e-04,
#          1.19560019e-03,  1.77112474e-03],
#        [ 2.09982259e-04,  2.93542268e-04,  4.23817847e-04,
#          1.59413359e-04,  1.34128909e-04],
#        [ 0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
#          0.00000000e+00,  0.00000000e+00]])}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

perm_sorted_idx = result.importances_mean.argsort()
#表示对数据进行从小到大进行排序，返回数据的索引值
#array([107,  25,  86,  85,  28,  84,  83,  82,  65,  81,  80,  79,  78,
#        76,  40,  75,  74,  34,  22,  87,  97, 104, 103, 102, 101, 100,
#        98,  19,   9,  95,  62,  17,  94,  93,  14,  91,  20,  72,   6,
#        96,  69,  77,  21,  29,  73,  89,  18,  16,  66,  53,  99,  15,
#        90,  70,  88,  36,  67,  61,  68,  71, 106,  41,  23,  31,  27,
#        59,  26,  57,  60,  24,  47,  13,  92,  52,  32,  30,  55, 105,
#        11,  39,  38,  37,   7,  50,  54,  51,  10,   8,  45,  44,  43,
#        12,  63,  49,  35,  48,  46,  64,  56,  42,  58,   1,   4,   5,
#         2,   0,   3,  33])
1
2
3
4
5
6
7
8
9
10
11

tree_importance_sorted_idx = np.argsort(clf.feature_importances_)
tree_indices = np.arange(0, len(clf.feature_importances_)) + 0.5

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))
ax1.barh(tree_indices,
         clf.feature_importances_[tree_importance_sorted_idx], height=0.7)
ax1.set_yticks(tree_indices)
ax1.set_yticklabels(X_train.columns[tree_importance_sorted_idx])
ax1.set_ylim((0, len(clf.feature_importances_)))
ax2.boxplot(result.importances[perm_sorted_idx].T, vert=False,
            labels=X_train.columns[perm_sorted_idx])
fig.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13

这里我们定义评估结果为auc，可以看到，最重要的特征进行shuffle之后对auc造成的变动也是最大的，而特征重要性为0的特征进行shuffle几乎不影响模型的效果。

缺陷
置换特征的重要性取决于对特征的改变，这会增加测量的随机性。重复置换后，结果可能会有很大差异。重复置换并在重复中对重要性值进⾏平均，可以鲁棒地度量结果，但会增加计算时间。

如果特征是相关的，则置换特征重要性可能会因不切实际的数据实例而有偏差。问题与部分依赖图相同：特征的置换在两个或多个特征关联时不会产⽣数据实例。当它们正相关时 (例如⼀个⼈的⾝⾼和体重)，并且我改变了其中⼀个特征时，我创建了不太可能甚⾄是物理上不可能的新实例 (例如，体重 2 公⽄的 2 ⽶体重的⼈)，但是我使⽤了这些新实例衡量重要性。换句话说，对于相关特征的置换特征重要性，我们考虑了当我们将特征与在现实中永远不会观察到的值交换时，模型性能会降低多少。检查特征是否紧密相关，如果是，对特征重要性的解释要⼩⼼。

另⼀个棘⼿的事情：添加相关特征可以通过在两个特征之间拆分重要性降低关联特征的重要性。

⼀个例⼦：比如我们要预测下⾬的概率，并将前⼀天上午8 点的温度⽤作特征，以及其他不相关的特征。我训练了⼀个随机森林，结果发现温度是最重要的特征，⼀切都很好，第⼆天晚上我睡得很好。现在想象另⼀个场景，其中我另外包括了上午 9 点的温度，它作为与上午 8 点的温度强相关的特征。如果我已经知道上午 8 点的温度，那么上午 9 点的温度不会给我太多其他信息。但是拥有更多特征总是好的，对吧？我⽤两个温度特征和不相关特征训练了另⼀个随机森林。随机森林中的⼀些树基于上午 8 点的温度，⼀些树基于上午 9 点的温度，⼀些则是同时拥有，还有⼀些则都没有。这两个温度特征⼀起⽐以前的单个温度特征具有更多的重要性，但是每个温度现在不在重要特征列表的顶部，⽽是在中间。通过引⼊相关特征，我将最重要的特征从重要性的顶端踢到了中间。上午 8 点的温度已经变得不那么重要了，因为该模型现在也可以依靠上午

9 点的测量值。另⼀⽅⾯，这使得特征重要性的解释变得相当困难。假设你要检查特征是否存在测量错误。检查费⽤昂贵，你决定只检查最重要特征中的前 3 个。在第⼀种情况下，你将检查温度，在第⼆种情况下，你将不包括任何温度特征，因为它们现在具有同等的重要性。即使重要性值在模型⾏为的层次上可能有意义，但如果你具有相关特征，则仍会造成混淆。

这是包括xgb，lgb在内的所有树模型统一都会存在的问题，即高相关特征会大大影响特征重要性的可信度，一般进行特征重要性计算之前都会先合并高相关特征的特征重要性。

基于代理模型的可解释

lime

直观上，lime的思路是解释模型行为的局部线性近似。虽然模型在全局范围内可能非常复杂，但在特定样本附近更容易对其进行近似。

在将模型视为黑盒的同时，我们扰乱了我们想要解释的样本，并围绕它学习了一个简单的可解释对的模型。上图比较直观的描述了这一点。模型的决策函数由蓝色/粉红色背景表示，明显是非线性的。明亮的红色十字是我们要解释的样本（我们称之为 X）。我们对 X 周围的样本进行采样，并根据它们与 X 的接近程度对它们进行加权（这里的权重由大小表示）。然后我们学习一个线性模型（虚线），它在 X 附近很好地近似模型，但不一定是全局的。

lime的诞生为后续的很多基于代理模型的可解释方法提供了很好的思路，例如，对于复杂的深度模型而言，我们可以使用其预测概率作为标签，然后使用原始特征作为特征，构建一个线性回归模型，然后通过线性回归模型的权重来间接解释深度模型

训练局部代理模型的方法也很直接简单：
1. 使用难以解释的复杂模型对样本进行预测，输出预测结果。
2. 选择一个简单的可解释模型例如线性模型或决策树来拟合原始样本特征和复杂模型的输出
此时，我们使用的线性模型或决策树就是我们的代理模型
3. 基于简单的可解释的代理模型来间接解释复杂模型

shap

这里我们引用shap作者在google上公开的例子，非常好理解shap的原理

假定以下情况：
你已经训练了机器学习模型来预测公寓价格。对于某套公寓，它的预计价格为 300,000 欧元，你需要对此做出解释。公寓的大小为 50 平⽅⽶，位于 2 楼，附近有公园，并且禁⽌猫⼊内：

所有公寓的平均预测价格为 310,000 欧元。与平均预测相⽐，每个特征值对预测有多少贡献？对于线性回归模型，答案很简单。每个特征的效应是特征的权重乘以特征值。这仅因模型的线性⽽起作⽤。对于更复杂的模型，我们需要不同的解决⽅案。例如，LIME 建议使⽤局部模型来估计特征效应。另⼀种解决⽅案来⾃合作博弈理论：Shapley 值 (由 Shapley (1953)[33] 创造) 是⼀种根据玩家对总⽀出的贡献分配⽀出给玩家的⽅法。玩家在联盟中进⾏合作，并从此合作中获得⼀定的收益。玩家？游戏？⽀出？与机器学习预测和可解释性有什么关系？“游戏” 是数据集单个实例的预测任务。“收益” 是此实例的实际预测值减去所有实例的平均预测值。“玩家” 是实例的特征值，它们协同⼯作以获得收益。在我们的公寓⽰例中，特征值 “公园附近”、“禁⽌猫进⼊”、“50 平⽅⽶” 和 “2 楼”

共同实现 300,000 欧元的预测。我们的⽬标是解释实际预测 (300,000 欧元) 与平均预测 (310,000 欧元) 之间的差额：-10,000 欧元。答案可能是：“公园附近” 贡献 30,000 欧元；“50 平⽅⽶” 贡献 10,000 欧元；“2 楼” 贡献 0 欧元；“禁⽌猫进⼊” 贡献 -50,000 欧元。贡献总计为 -10,000 欧元，即最终预测减去平均预测公寓价格。我们如何计算⼀个特征的 Shapley 值？Shapley 值是所有可能的联盟 (Coalition) （特征组合）中特征值的平均边际贡献。在下图中，我们评估了将 “禁⽌猫进⼊” 添加到 “公园附近” 和 “50 平⽅⽶” 组成的联盟中时的贡献。我们通过从数据中随机绘制另⼀套公寓，模拟出只有 “公园附近”、“禁⽌猫进⼊” 和 “50 平⽅⽶” 在⼀个联盟中，并将它的值⽤于楼层特征。“2 楼” 被随机抽取的 “1 楼” 所取代，然后我们预测这个组合的公寓价格 (310,000 欧元)。在第⼆步中，我们将 “禁⽌猫进⼊” 从联盟中删除，从随机绘制的公寓中将猫允许/禁⽌进⼊的特征值替换。在这个随机⽰例中为 “允许猫进⼊”，但也可能再是 “禁⽌猫进⼊”。我们预测对 “公园附近” 和 “50 平⽅⽶” 联盟的公寓价格 (320,000 欧元)。“禁⽌猫进⼊” 的贡献 310,000 - 320,000 = -10.000 欧元。此估计取决于⽤作猫和楼层特征值的 “贡献者”的随机绘制的值。如果我们重复此采样步骤并平均贡献，将会得到更好的估计。

我们对所有可能的联盟重复此计算。Shapley 值是对所有可能的联盟的所有边际贡献的平均值。

上图显⽰了确定 “禁⽌猫进⼊” 的 Shapley 值所需的所有特征值联盟。第⼀⾏显⽰没有任何特征值的联盟。第⼆，第三和第四⾏显⽰随联盟⼤⼩增加⽽不同的联盟，以 “|” 分隔。总⽽⾔之，可能的联盟如下：
•空(用所有样本的特征进行均值计算，将均值计算的结果来作为一种近似的空的一种体现)
• “公园附近”
• “50 平⽅⽶”
• “2 楼”
• “公园附近”+“50 平⽅⽶”
• “公园附近”+“2 楼”
• “50 平⽅⽶”+“2 楼”
• “公园附近”+“50 平⽅⽶”+“2 楼”

对于这些联盟中的每个联盟，我们都计算带有或不带有特征值 “禁⽌猫进⼊” 的预测公寓价格，并取其差值以获得边际贡献。Shapley 值是边际贡献的 (加权) 平均值。我们⽤公寓数据集中的随机特征值替换不在联盟中的特征的特征值，以从机器学习模型中获得预测。

样本层面的可解释

样本层面的可解释方法绝大多数都和cv中的分析相关，这里就不赘述了

工业界的一些可解释思路

模型可解释性在中国人寿保险理赔反欺诈中的实践

人寿保险的这个可解释机器学习的应用场景主要是面向客诉和监管要求的，即对于申请理赔的用户，如果根据模型判定其为欺诈，则不进行理赔，则客户大概率会投诉相关部门诉诸法律，那么面对客诉问题，我们就需要解释模型为何将其预测为欺诈用户，在分享的案例中，人寿的做法还是比较中规中矩的，没有太多变化，基本上就是直接使用原生的shap来对客诉的样本进行模型预测的解释，shap最终的效果其实本质上就是把复杂模型统统使用类lr的方式来解释，例如某个用户被判定为欺诈的原因在于某个feature过高或者某些feature过低等等，那么根据shap反馈的结果，算法工程师将对应的高贡献度的特征反馈给审核员，由审核员来整理相应的话术反馈客诉用户,从而完成对客诉的回应。

除此之外，

根据shap反馈的结果，算法工程师可以确定哪些特征是具有重要的业务意义的，将这些特征反馈给业务人员，业务人员根据自身的业务知识积累，对这些特征进行业务层面的分析，从而形成新的知识

度小满的子评分卡思路

度小满的子评分卡集成的思路是一个非常好的方法，虽然严格意义上来说，并没有使用到典型的shap，lime，deeplift这类复杂的可解释性方法，但是对于实际的应用来说，帮助很大，因为实现上简单，并且从思路上来看，也可以在很大程度上折衷模型性能和可解释性的问题

不过这种思路也依赖于百度本身庞大的多源数据和实力，包括了用户的app行为数据，位置移动数据（依赖于百度地图），征信报告和运营商数据（依赖于度小满本身的较为充裕的现金流，毕竟像征信报告数据价值不菲），那么子评分卡集成的思路其实也非常的巧妙：

• 1.对于多源数据的建模方法，百度使用了简单的，每个源的数据单独建模的思路，例如app行为数据这类的时序数据使用时序类模型构建，征信报告数据使用常规的gbdt模型来构建，运营商数据可以使用图模型来构建。。。对于不同源的数据使用相适应的模型来进一步榨取不同模态数据的价值；
• 2.将不同源的模型的输出进行stacking集成，meta 学习器使用简单的逻辑回归或决策树，不得不说，是一个妙招，不仅仅在很大程度上提供了较好的可解释性（逻辑回归可以直接解释用户被判定为坏用户是由于上图哪个分偏高或偏低导致的，从而在一定程度上让建模人员和业务人员都能快速定位和了解某个用户被判定为坏用户的主要原因），stacking集成了多个复杂模型的输出，一定程度上通过集成的方式来提升总模型的效果，这也是比赛中比较常用的套路了~