热门标签
热门文章
- 1flutter开发实用技巧_flutter开发技巧
- 2哥斯拉还原加密流量_ctf misc 哥斯拉流量解密脚本
- 3Flutter-仿腾讯视频Banner效果
- 4Android 实现Activity后台运行_startactivity 在后台允许
- 5时序预测 | MATLAB实现SVM(支持向量机)时间序列多步预测_matlab的支持向量机时间序列预测
- 6conda创建python虚拟环境
- 7Delphi Professional Crack,IDE插件开发和扩展IDE_delphi ide扩展
- 8哔哩哔哩android4.3,哔哩哔哩(tv.danmaku.bili) - 6.26.0 - 应用 - 酷安
- 9python编程与ai计算大数据分析_python只是一门做数据分析与人工智能的编程语言吗?你有什么其他看法?...
- 10一口气搞懂「Flink Metrics」监控指标和性能优化,全靠这33张图和7千字(建议收藏)_flink metrics详细
当前位置: article > 正文
【图论】树链剖分
作者:从前慢现在也慢 | 2024-03-15 18:09:51
赞
踩
【图论】树链剖分
本篇博客参考:
基本概念
首先,树链剖分是什么呢?
简单来说,就是把一棵树分成很多条链,然后利用数据结构(线段树、树状数组)维护链上的信息
下面是一些定义:
- 重子结点:父亲结点的所有儿子结点中子树结点数目最多的结点称为重子结点
- 轻子结点:父亲结点的所有儿子中除了重子结点的其他结点称为轻子结点
如果某个结点是叶子结点,那么它既没有重子结点也没有轻子结点
- 重边:父亲结点和重子结点连成的边
- 轻边:父亲结点和轻子结点连成的边
- 重链:多条重边连接成的链
- 轻链:多条轻边连接成的链
落单的点也当做重链,那整棵树就会被分成若干条重链,类似这样:(图源Oi Wiki)
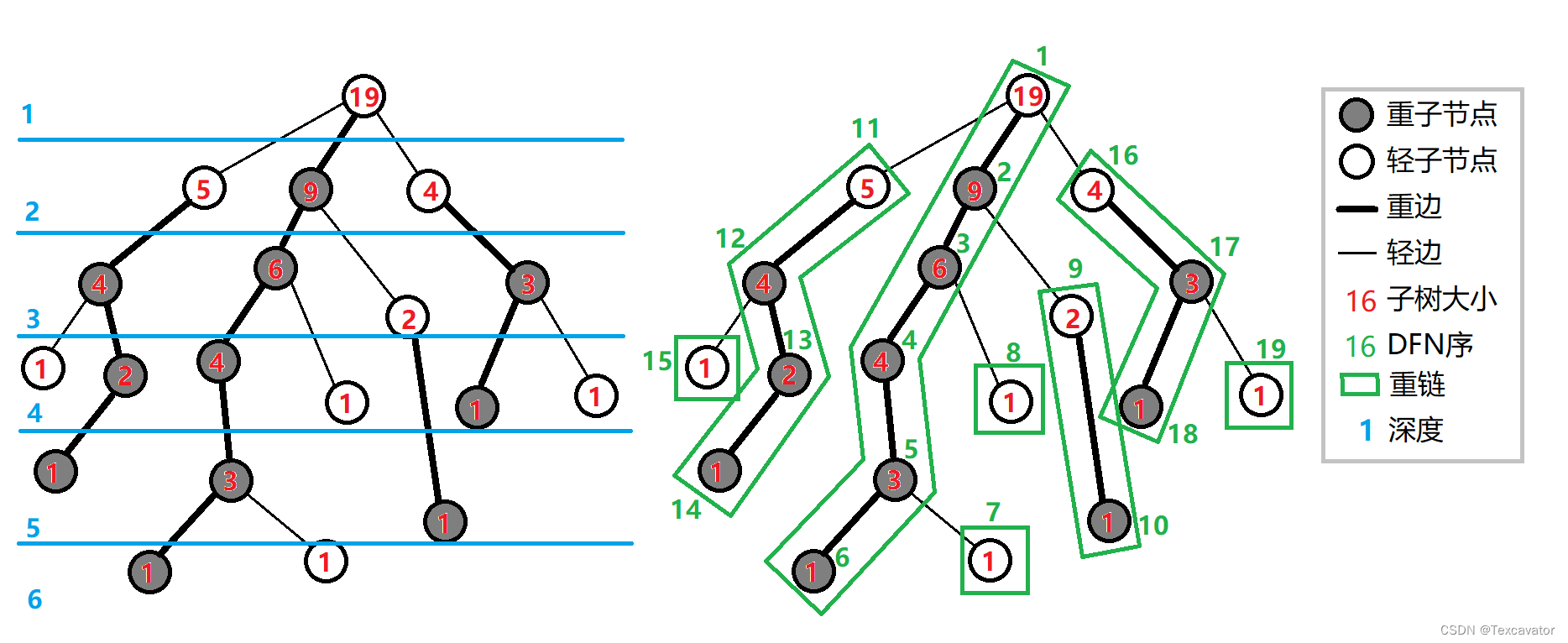
下面是一些变量声明:
fa[u]结点 u 的父亲结点dep[u]结点 u 的深度sz[u]以结点 u 为根的子树的结点个数son[u]结点 u 的重儿子top[u]结点 u 所在链的顶端结点dfn[u]结点 u 在 dfs 中的执行顺序,同时也是树链剖分后的新编号,可以理解为dfs序的映射id[u]dfn 标号 u 对应的结点编号,有id[dfn[u]] == u
树链剖分的一些性质
- 重链开头的结点不一定是重子结点(因为每一个非叶子结点不管是重子结点还是轻子结点都有重边)
- 剖分时重链优先遍历,最后的 dfs 序中(也就是
dfn数组),重链的 dfs 序时连续的,按 dfs 序排序后的序列就是剖分后的链 - 时间复杂度 O ( l o g n ) O(logn) O(logn)
代码实现
接下来需要实现树链剖分,也就是把每个结点划到一条链里,这通常是由两边 dfs 来实现的
第一遍 dfs
目的:处理 fa[u] dep[u] sz[u] son[u]
void dfs1(int u, int father, int depth) // u: 当前结点 fa: 父结点 depth: 当前深度
{
fa[u] = father; // 更新当前结点父结点
dep[u] = depth; // 更新当前结点深度
sz[u] = 1; // 子树大小初始化为1
for (int i = 0; i < g[u].size(); i ++ )
{
int j = g[u][i]; // 子结点编号
if (j == father) continue;
dfs1(j, u, depth + 1);
sz[u] += sz[j]; // 用子结点的sz更新父结点的sz
if (sz[j] > sz[son[u]]) son[u] = j; // 更新重子结点
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
第二遍 dfs
目的:处理 top[u] dfn[u] id[u]
void dfs2(int u, int tt) // u: 当前结点 tt: 重链顶端结点 { top[u] = tt; // 更新当前结点所在重链顶端 dfn[u] = ++ cnt; // 更新dfs序 id[cnt] = u; // 更新dfs序的映射 if (!son[u]) return; // 叶子结点 直接退出 // 优先遍历重子结点 目的是保证链上各个结点的dfs序连续 // 当前结点的重子结点和当前结点在同一条链上 所以链的顶端都是tt dfs2(son[u], tt); for (int i = 0; i < g[u].size(); i ++ ) { int j = g[u][i]; // 子结点编号 if (j == son[u] || j == fa[u]) continue; // 遇到重子结点或者父结点就跳过 dfs2(j, j); // j点位于轻链顶端 它的top必然是本身 } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
常见应用
两遍 dfs 之后,就已经完成了树链剖分的操作,但是由于本人举一反三能力缺失根本不知道应该怎么用,所以后面再放几个常见的使用情况
路径维护:求树上两点路径权值和
这里做的是一个类似LCA的操作,如果两个结点不在同一条链上,就让深度更大的结点往上跳(每次只能跳一个结点,避免两个结点一起跳导致擦肩而过)直到跳到同一条链上,因为同一条链上的点 dfs 序是相邻的,所以可以直接在这条链上用数据结构计算权值和(下面的代码用的是线段树)
int sum(int x, int y) // xy表示待求的两点路径权值和 { int ans = 0; int tx = top[x], ty = top[y]; // tx ty分别表示x和y所在重链的顶端结点 while (tx != ty) // 让x和y跳到同一条链上 { if (dep[x] >= dep[y]) // x比y更深 让x先跳 { ans += query(dfn[tx], dfn[x]); // query是线段树的区间求和函数 x = fa[tx], tx = top[x]; // 让x跳到原先链顶端的父结点 更新tx } else { ans += query(dfn[ty], dfn[y]); // query是线段树的区间求和函数 y = fa[ty], ty = top[y]; // 让y跳到原先链顶端的父结点 更新ty } } // 循环结束 x和y终于到了同一条链 但是二者不一定是同一个结点 所以还需要计算两点之间的贡献 if (dfn[x] <= dfn[y]) ans += query(dfn[x], dfn[y]); else ans += query(dfn[y], dfn[x]); return ans; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
路径维护:改变两点最短路径上的所有点的权值
和上面的求最短路径权值和很像,都是先让两个点跳到同一条链上再进行计算
void update(int x, int y, int c) // 把x与y的最短路上所有点的权值都加上c { int tx = top[x], ty = top[y]; while (tx != ty) { if (dep[tx] >= dep[ty]) { modify(dfn[tx], dfn[x], c); // modify是线段树区间修改的函数 x = fa[tx], tx = top[x]; // 让x跳到原先链顶端的父结点 更新tx } else { modify(dfn[ty], dfn[y], c); // modify是线段树区间修改的函数 y = fa[ty], ty = top[y]; // 让y跳到原先链顶端的父结点 更新ty } } // 循环结束 x和y终于到了同一条链 但是二者不一定是同一个结点 所以还需要对两点之间的结点进行修改 if (dfn[x] <= dfn[y]) modify(dfn[x], dfn[y], c); else modify(dfn[y], dfn[x], c); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
求最近公共祖先
思路就是,如果两个点不在一条重链上,那就不断让深度大的结点往上跳,直到跳到同一条链上,那么深度较小的点就是LCA
int lca(int u, int v) // 求u和v的lca
{
while (top[u] != top[v]) // 如果u和v不在同一条链上就一直让深度大的点往上跳
{
if (dep[top[u]] > dep[top[v]]) u = fa[top[u]];
else v = fa[top[v]];
}
return dep[u] > dep[v] ? v : u; // 深度小的结点就是lca
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/243509
推荐阅读
相关标签



