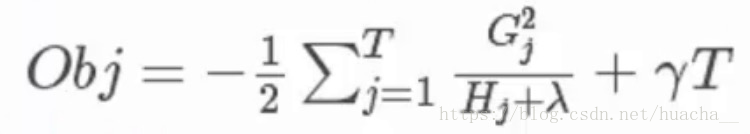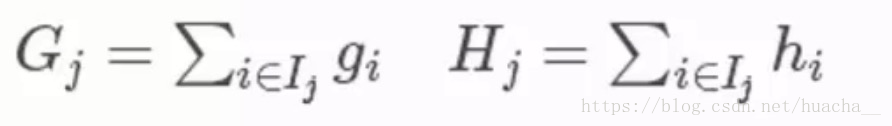【机器学习】XGBoost集成算法——（理论+图解+python代码比较其他算法使用天池蒸汽数据）_集成算法示意图

一、集成算法思想

二、XGBoost基本思想

三、用python实现XGBoost算法

---

在竞赛题中经常会用到XGBoost算法，用这个算法通常会使我们模型的准确率有一个较大的提升。既然它效果这么好，那么它从头到尾做了一件什么事呢？以及它是怎么样去做的呢？

我们先来直观的理解一下什么是XGBoost。XGBoost算法是和决策树算法联系到一起的。 

XGBoost是boosting算法的其中一种。Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器。因为XGBoost是一种提升树模型，所以它是将许多树模型集成在一起，形成一个很强的分类器。而所用到的树模型则是CART回归树模型

一、集成算法思想

在决策树中，我们知道一个样本往左边分或者往右边分，最终到达叶子结点，这样来进行一个分类任务。 其实也可以做回归任务。

该算法思想就是不断地添加树，不断地进行特征分裂来生长一棵树，每次添加一个树，其实是学习一个新函数，去拟合上次预测的残差。当我们训练完成得到k棵树，我们要预测一个样本的分数，其实就是根据这个样本的特征，在每棵树中会落到对应的一个叶子节点，每个叶子节点就对应一个分数，最后只需要将每棵树对应的分数加起来就是该样本的预测值

 

如下图例子，训练出了2棵决策树，小孩的预测分数就是两棵树中小孩所落到的结点的分数相加。爷爷的预测分数同理

 

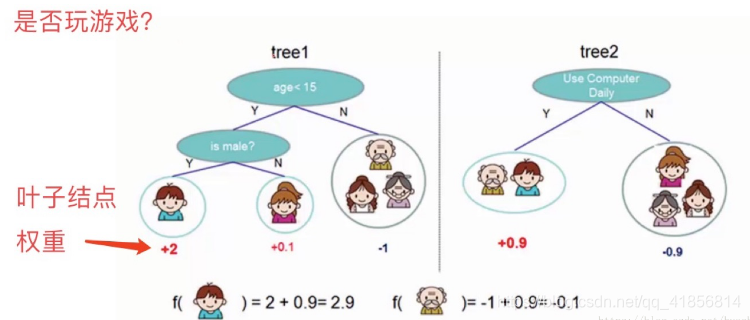
看上面一个图例左边：有5个样本，现在想看下这5个人愿不愿意去玩游戏，这5个人现在都分到了叶子结点里面，对不同的叶子结点分配不同的权重项，正数代表这个人愿意去玩游戏，负数代表这个人不愿意去玩游戏。所以我们可以通过叶子结点和权值的结合，来综合的评判当前这个人到底是愿意还是不愿意去玩游戏。上面「tree1」那个小男孩它所处的叶子结点的权值是+2（可以理解为得分）。

用单个决策树好像效果一般来说不是太好，或者说可能会太绝对。通常我们会用一种集成的方法，就是一棵树效果可能不太好，用两棵树呢？

看图例右边的「tree2」，它和左边的不同在于它使用了另外的指标，出了年龄和性别，还可以考虑使用电脑频率这个划分属性。通过这两棵树共同帮我们决策当前这个人愿不愿意玩游戏，小男孩在「tree1」的权值是+2，在「tree2」的权值是+0.9， 所以小男孩最终的权值是+2.9（可以理解为得分是+2.9）。老爷爷最终的权值也是通过一样的过程得到的。

所以说，我们通常在做分类或者回归任务的时候，需要想一想一旦选择用一个分类器可能表达效果并不是很好，那么就要考虑用这样一个集成的思想。上面的图例只是举了两个分类器，其实还可以有更多更复杂的弱分类器，一起组合成一个强分类器。

 

二、XGBoost基本思想

XGBoost的集成表示是什么？怎么预测？求最优解的目标是什么？看下图的说明你就能一目了然。

600

在XGBoost里，每棵树是一个一个往里面加的，每加一个都是希望效果能够提升，下图就是XGBoost这个集成的表示（核心）。

一开始树是0，然后往里面加树，相当于多了一个函数，再加第二棵树，相当于又多了一个函数...等等，这里需要保证加入新的函数能够提升整体对表达效果。提升表达效果的意思就是说加上新的树之后，目标函数（就是损失）的值会下降。

如果叶子结点的个数太多，那么过拟合的风险会越大，所以这里要限制叶子结点的个数，所以在原来目标函数里要加上一个惩罚项「omega(ft)」。

 

这里举个简单的例子看看惩罚项「omega(ft)」是如何计算的：

一共3个叶子结点，权重分别是2，0.1，-1，带入「omega(ft)」中就得到上面图例的式子，惩罚力度和「lambda」的值人为给定。

XGBoost算法完整的目标函数见下面这个公式，它由自身的损失函数和正则化惩罚项「omega(ft)」相加而成。

关于目标函数的推导本文章不作详细介绍。过程就是：给目标函数对权重求偏导，得到一个能够使目标函数最小的权重，把这个权重代回到目标函数中，这个回代结果就是求解后的最小目标函数值，如下：

其中第三个式子中的一阶导二阶导的梯度数据都是可以算出来的，只要指定了主函数中的两个参数，这就是一个确定的值。下面给出一个直观的例子来看下这个过程。

（这里多说一句：Obj代表了当我们指定一个树的结构的时候，在目标上最多会减少多少，我们可以把它叫做结构分数，这个分数越小越好）

对于每次扩展，我们依旧要枚举所有可能的方案。对于某个特定的分割，我们要计算出这个分割的左子树的导数和和右子数导数和之和（就是下图中的第一个红色方框），然后和划分前的进行比较（基于损失，看分割后的损失和分割前的损失有没有发生变化，变化了多少）。遍历所有分割，选择变化最大的作为最合适的分割。

 

 GBDT与XGbost的区别

三、用python实现XGBoost算法代码

使用天池竞赛的蒸汽数据

xgboost回归对比线性回归 Ada、 GradientBoostingRegressor

 
train = pd.read_csv('./zhengqi_train.txt',sep = '\t')
 
X = train.iloc[:,0:-1]
y = train['target']
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size =0.2)
 
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
 
linear = LinearRegression()
linear.fit(X_train,y_train)
 
print('r2_score',linear.score(X_test,y_test))
y1_ = linear.predict(X_test)
mean_squared_error(y_test,y1_)

r2_score 0.9035544162615812

from sklearn.ensemble import AdaBoostRegressor
ada = AdaBoostRegressor()
ada.fit(X_train,y_train)
 
print('ada_score',ada.score(X_test,y_test))
y2_ = ada.predict(X_test)
mean_squared_error(y_test,y2_)

ada_score 0.8469280190502533

0.15315981475425688

from xgboost import XGBRegressor
xgb = XGBRegressor()
xgb.fit(X_train,y_train)
 
print('xgb_score',xgb.score(X_test,y_test))
y3_ = xgb.predict(X_test)
mean_squared_error(y_test,y3_)

xgb_score 0.896815295803221

0.10324391232279032

from sklearn.ensemble import GradientBoostingRegressor
gbdt = GradientBoostingRegressor()
gbdt.fit(X_train,y_train)
 
print('gbdt_score',gbdt.score(X_test,y_test))
y4_ = gbdt.predict(X_test)
mean_squared_error(y_test,y4_)

gbdt_score 0.8947755352826943

0.10528484327258612

推荐：

一文读懂机器学习大杀器XGBoost原理