二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

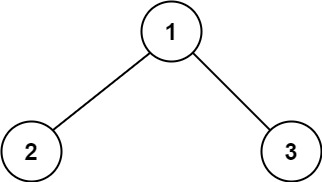
给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：
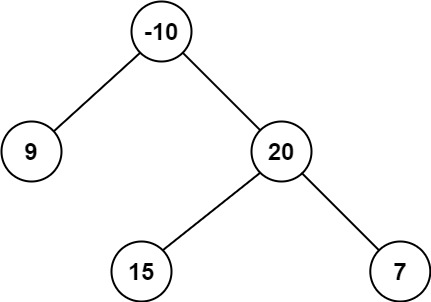
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

解题思路

定义一个递归函数，这个函数计算通过当前节点的单边最大路径和，即从当前节点出发，到达任意叶子节点的最大路径和。这里的“单边”意味着路径只能从父节点到左子节点或右子节点，不能同时包含两边。
在递归过程中，计算包含当前节点和至多一个子节点的最大路径和。
更新全局最大路径和。这一步很关键，对于每个节点，我们计算通过该节点的最大路径和，这条路径可以包含该节点的左右子节点。然后，我们比较并更新记录的全局最大路径和。
递归的终止条件是遍历到空节点，此时返回0。
递归函数返回当前节点值加上左右子节点中的最大单边路径和，但如果单边路径和为负数，则可以选择不包含任何子节点，因为不选择比选择负数路径和更优。

完整代码

Python


# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.max_sum = float('-inf')
 
        def max_gain(node):
            if not node:
                return 0
 
            # 计算左右子树的最大单边路径和
            left_gain = max(max_gain(node.left), 0)
            right_gain = max(max_gain(node.right), 0)
 
            # 更新全局最大路径和
            price_newpath = node.val + left_gain + right_gain
            self.max_sum = max(self.max_sum, price_newpath)
 
            # 返回包含当前节点的最大单边路径和
            return node.val + max(left_gain, right_gain)
 
        max_gain(root)
        return self.max_sum

Java


/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int maxSum = Integer.MIN_VALUE;
 
    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }
    public int maxGain(TreeNode node) {
        if (node == null) return 0;
 
        // 计算左右子树的最大单边路径和
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);
 
        // 更新全局最大路径和
        int newPathPrice = node.val + leftGain + rightGain;
        maxSum = Math.max(maxSum, newPathPrice);
 
        // 返回包含当前节点的最大单边路径和
        return node.val + Math.max(leftGain, rightGain);
    }
}

125. 验证回文串

如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。

字母和数字都属于字母数字字符。

给你一个字符串 s，如果它是 回文串 ，返回 true ；否则，返回 false 。

示例 1：
输入: s = "A man, a plan, a canal: Panama"
输出：true
解释："amanaplanacanalpanama" 是回文串。
示例 2：
输入：s = "race a car"
输出：false
解释："raceacar" 不是回文串。
示例 3：
输入：s = " "
输出：true
解释：在移除非字母数字字符之后，s 是一个空字符串 "" 。
由于空字符串正着反着读都一样，所以是回文串。

解题思路

清理字符串：首先，我们需要移除字符串中所有非字母数字的字符，并将所有大写字母转换为小写字母。这可以通过遍历字符串，并使用字符判断函数来实现。
双指针法检查回文：然后，我们可以使用双指针法来检查处理后的字符串是否是回文。一个指针从字符串的开始向前移动，另一个指针从字符串的末尾向后移动，逐个比较两个指针所指的字符，直到两个指针相遇。如果在任何时候字符不匹配，那么字符串就不是回文串。
返回结果：如果所有的字符都匹配了，那么就返回 true，表示字符串是一个回文串；否则，返回 false。

完整代码

Python


class Solution:
    def isPalindrome(self, s: str) -> bool:
        # 清理字符串，只保留字母数字字符，并转换为小写
        clean_s = "".join(ch.lower() for ch in s if ch.isalnum())
 
        # 双指针法检查回文
        left, right = 0, len(clean_s) - 1
        while left < right:
            if clean_s[left] != clean_s[right]:
                return False
            left, right = left + 1, right - 1
 
        return True

Java


public class Solution {
    public boolean isPalindrome(String s) {
        // 清理字符串，只保留字母数字字符，并转换为小写
        String cleanS = s.replaceAll("[^A-Za-z0-9]", "").toLowerCase();
 
        // 双指针法检查回文
        int left = 0, right = cleanS.length() - 1;
        while (left < right) {
            if (cleanS.charAt(left) != cleanS.charAt(right)) {
                return false;
            }
            left++;
            right--;
        }
 
        return true;
    }
}

127. 单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
sk == endWord

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

示例 1：
输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2：
输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

解题思路

预处理：首先，对给定的单词列表进行预处理，将每个单词通过替换其中的一个字母为通配符（例如，''）的方式，转换为所有可能的中间状态。这样做可以帮助我们快速找到只差一个字母的所有单词。例如，对于单词 "hot"，它的中间状态可以是 "ot", "ht", "ho"。
初始化队列：初始化一个队列，将起始单词 beginWord 及其对应的转换步数（1）作为初始元素加入队列。
广度优先搜索：然后，进行广度优先搜索：
- 从队列中弹出一个元素（当前单词及其步数）。
- 遍历当前单词的所有中间状态，对于每个中间状态，获取所有可能的下一个单词。
- 如果下一个单词是 endWord，那么找到了最短路径，返回当前单词的步数加一。
- 否则，如果下一个单词没有被访问过，将其及其对应的步数加一后加入队列。
- 标记当前单词为已访问。
返回结果：如果队列被全部遍历后仍未找到 endWord，则返回 0。

完整代码

Python


class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        if endWord not in wordList:
            return 0
 
        L = len(beginWord)
 
        # 所有单词的通用状态
        all_combo_dict = defaultdict(list)
        for word in wordList:
            for i in range(L):
                all_combo_dict[word[:i] + "*" + word[i+1:]].append(word)
 
        # 队列用于广度优先搜索，队列中元素是 (当前单词, 转换次数)
        queue = deque([(beginWord, 1)])
        # 访问过的单词
        visited = {beginWord: True}
        while queue:
            current_word, level = queue.popleft()
            for i in range(L):
                # 当前单词的通用状态
                intermediate_word = current_word[:i] + "*" + current_word[i+1:]
 
                # 通用状态对应的所有单词
                for word in all_combo_dict[intermediate_word]:
                    # 如果找到了目标单词
                    if word == endWord:
                        return level + 1
                    # 否则，如果没访问过，加入队列
                    if word not in visited:
                        visited[word] = True
                        queue.append((word, level + 1))
                all_combo_dict[intermediate_word] = []  # 清空访问过的通用状态
        return 0

Java


public class Solution {
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        if (!wordList.contains(endWord)) return 0;
 
        int L = beginWord.length();
 
        Map<String, List<String>> allComboDict = new HashMap<>();
        wordList.forEach(
            word -> {
                for (int i = 0; i < L; i++) {
                    String newWord = word.substring(0, i) + '*' + word.substring(i + 1, L);
                    List<String> transformations =
                        allComboDict.getOrDefault(newWord, new ArrayList<>());
                    transformations.add(word);
                    allComboDict.put(newWord, transformations);
                }
            });
 
        Queue<Pair<String, Integer>> Q = new LinkedList<>();
        Q.add(new Pair(beginWord, 1));
 
        Map<String, Boolean> visited = new HashMap<>();
        visited.put(beginWord, true);
 
        while (!Q.isEmpty()) {
            Pair<String, Integer> node = Q.remove();
            String word = node.getKey();
            int level = node.getValue();
            for (int i = 0; i < L; i++) {
 
                String newWord = word.substring(0, i) + '*' + word.substring(i + 1, L);
 
                for (String adjacentWord : allComboDict.getOrDefault(newWord, new ArrayList<>())) {
                    if (adjacentWord.equals(endWord)) {
                        return level + 1;
                    }
                    if (!visited.containsKey(adjacentWord)) {
                        visited.put(adjacentWord, true);
                        Q.add(new Pair(adjacentWord, level + 1));
                    }
                }
            }
        }
 
        return 0;
    }
}

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/329448