- 1windows安装cuda_cuda版本选择
- 2Hadoop的安装与伪分布式学习_安装与配置hadoop分布式环境。可以选择本机安装虚拟机,或者完成头歌在线实训
- 3iphone手机 ios系统 无法更新app 跳转到AppStore 显示 打开_苹果手机软件提示升级但点开是打开
- 4MSTP笔记_对于mstp设备来说,服务层路径是存在于网管侧的路径,而客户层路径是存在于网元侧的
- 5nvidia-smi 无进程占用GPU,但GPU显存却被占用_gpu用户只占用4g,但是nvidia-smi显示占用显存用了6g
- 6「雕爷学编程」Arduino动手做(32)——雨滴传感器模块_雨滴传感器代码
- 7Docker中安装Gitlab详细全教程_docker安装gitlab
- 8区块链安全初探(二):区块链的层次
- 9【LeetCode】单链表——刷题
- 102022年最新版Android安卓面试题+答案精选(每日20题,持续更新中)【三】_安卓数据库交互面试
word2vec的原理和难点介绍(skip-gram,负采样、层次softmax)
赞
踩
前言
本文仅作一个备忘录,不详细说明word2vec的两种词袋模型(skip-gram和CBOW),后面的记录默认是在skip-gram的基础下完成,即是利用中心词来预测上下文;同时也不涉及数学的推导计算,仅是做一些我认为比较重要的知识纪要。
既然word2vec是讲文本的向量化,那么本文中都以下面这句话作为案例讲解
this cat is very cute.
word2vec是什么?
word2vec通常是一种进行文本的向量提取的技术,利用单词的共现(共同出现,后续会有详细记录)思想,通过对文本语料库进行训练,得到的每个单词的向量,在应用的过程中,就可以通过单词向量来计算单词的相似性,或者说是共现概率。概率大表示单词之间比较相似。
在word2vec算法中,内部是基于两种词袋模型进行展开的,一种是skip-gram,另一种是CBOW,本文中都是基于skip-gram的基础下做讲解,即是利用中心词来预测上下文。
下面会一步一步的讲解是如何通过skip-gram结合单词的共现思想来实现word2vec的。
skip-gram简单介绍
skip-gram原理就是通过中心词来预测上下文词汇,比如下图

假设is为中心词,那么其他词就可以通过is来预测得到。
但是疑问在于
- 这个范围是多大呢?is的所有词汇都能预测吗?还是只能预测cat和very呢?
这个是可以人为设定的
- 通过人为指定滑窗大小,如果滑窗大小为2,那么以is为中心的左右两个单词都可以通过is来预测得到,以此类推。当然在模型训练的过程中,滑窗是不断的滚动的,所以每一个词都会成为中心词汇。这就是skip-gram的朴素理解。
本文中我们假设设定skip-gram的滑窗大小是2,那么在滑窗滑的过程中,当is为中心词时,就可以通过is去预测周围四个词。所以我们直觉的绘制出的一个简易的流程图。
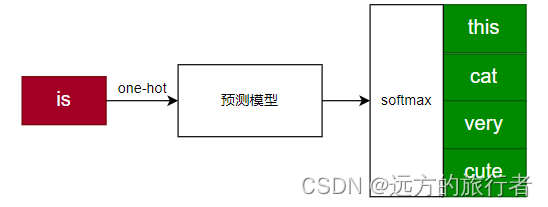
从以上的简单图例中可以简单的做个思考:
- 这个模型应该是一个多分类模型,因为要通过is去预测多个分类;
- 这个模型的label是什么?是this,cat,very,cute吗,这个label该怎么表达?
word2vec是有监督还是无监督?
word2vec可以说是无监督,因为他全程并不需要我们去标定label,label是内部自己生成和判定的,那问题就产生了。
问题:
- 这个label如何产生呢?
这个问题也伴随着我们在skip-gram中的第二个思考:当is是中心词时,模型的label是this,cat,very,cute吗?下面就会解答这个问题。
模型输入的数据是什么、是以什么形式输入(共现思想)?
上面我们甩出了一个图,是通过我们对skip-gram的直觉理解随手画的一个图,输入是is,输出是周边四个词的预测概率,这个思想是对的,但是它现在这么看有点像是有监督学习,this,cat等就是label,所以我们如何将其转变为无监督学习的表达方式呢?
既然要改变表达方式,那么模型的输入的训练数据就不能是is了,那这个训练的data是什么?或者说输入的特征数据是什么?以下面这句话为例
this cat is very cute.
word2vec是直接一次将这句话输入到模型中吗?显然不是,倘若我们指定的滑窗大小是2,则产生的语料是:
当以this为中心词:this cat is
当以cat 为中心词:this cat is very
当以is为中心词: this cat is very cute
注:以上并未考虑去除停用词,以及一些高频的系动词和冠词,只是做一个简单的举例用以描述具体原理。那为啥停用词和高频系动词、冠词等要去掉呢?停用词肯定不用说了,都不用了还训练干啥,而高频的系动词冠词这些词可以认为它和谁一起出现的概率都很高,所以导致本身对模型没啥价值,模型根本不会学到啥,所以也可以考虑去掉。
下面接着正题
当以cat为中心词时,得到了语料是‘this cat is very’,最常规的做法就是利用cat去挨个预测其他词了,也是我们在skip-gram中根据本能直觉绘制的那个图。
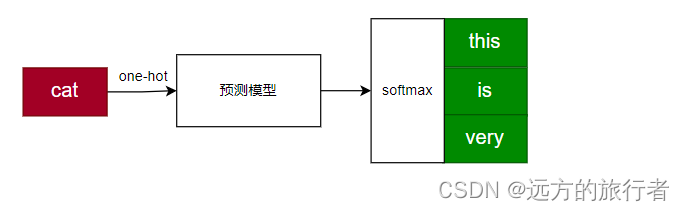
显然这就是一个多分类的问题了,我们可以做一个简单的思考纪要
| 1.这个模型应该是一个多分类模型,因为要通过is去预测多个分类; |
|---|
| 2.这个模型的label是什么?是this、is、very吗,这个label该怎么表达? |
但是word2vec并不这么做,最开始我们提到了word2vec是利用了单词的共现思想,这个共现其实就是在这里得以体现,当以cat作为中心词时:模型输入的是:
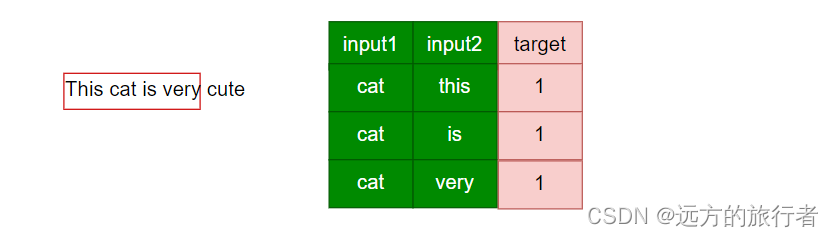
这里的cat,this表示,他们一起在滑窗中出现,这就是共现,后面的1就是label,表示一起出现的概率,这就是在无监督学习中label的产生方式,当然label为1的是正样本。以此类推,其他的正样本产生方式也是一样的道理。那么这也就解释了我们在word2vec中的遗留的问题和skip-gram中遗留的思考。
表1:this为中心词
表2:cat为中心词
表3:is为中心词
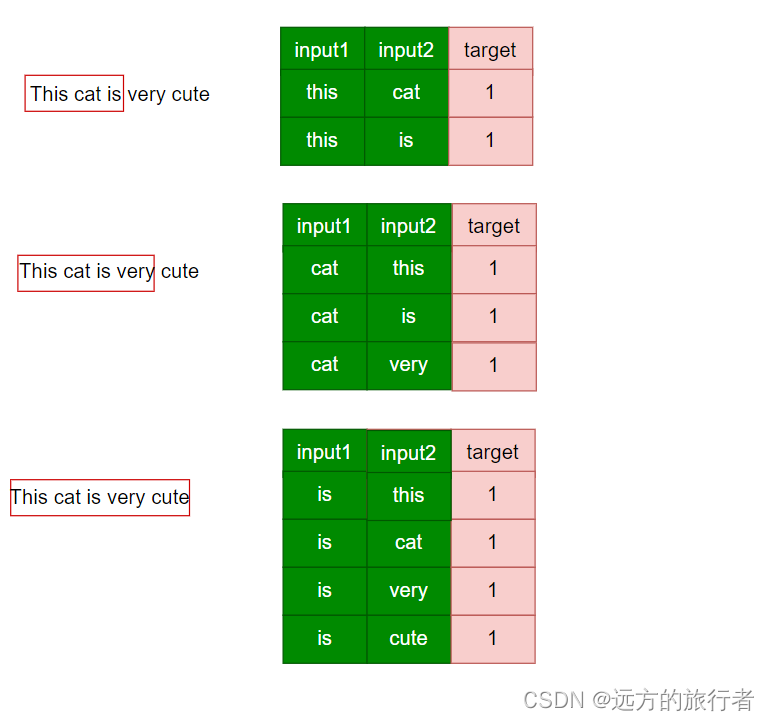
所以最后就可以做一个总结:
- 模型的输入的训练数据是两个单词;
- 模型的label是对应的两个单词一起出现的概率,正样本的label为1,负样本的label为0。
负样本生成
正样本我们知道如何产生了, 那负样本是什么呢,负样本就是以cat为中心词时,未出现在滑窗中的所有词和中心词的组合,比如 cat cute就是负样本,label应该为0。
当然这里有个问题:就是,语料库是非常大的,当我们进行样本获取的时候,如果语料库是10w,这时候,滑窗内的词是正样本,滑窗外都是负样本,那每一次滑窗移动,负样本都会非常大。这显然是效率很低,甚至不利于训练,该怎么处理?这就是后续word2vec优化中的其中一步。
word2vec的参数是什么?
在模型训练中,word2vec是一个神经网络,那它最终的参数是代表着什么呢,它是什么样子的形式呢?
在word2vec训练过程中,它的参数其实最终就是两个矩阵,假设这里将这两个矩阵分别叫做A,B。每一行就是一个单词的向量表示,
那这里有个疑问:为啥是两个参数矩阵
这里做一个朴素的理解,这里面的A、B矩阵都有所有词的向量,但是他们又不太相同,比如cat在A矩阵中有个对应的向量参数(也就是矩阵的一行),同样在B中也有一行,为什么会这样,可以理解为,A矩阵里的cat对应的那一行向量(也就是参数)是当cat作为中心词时会对其进行更新的和学习的,B矩阵里的cat对应的那一行向量(也就是参数)当cat作为非中心词时会对其进行更新的和学习的。这是不一样的。
当然又会有疑问:最终训练出的模型中,我们要采用哪一个矩阵里的参数作为单词的embedding向量呢?
其实这是个开放的问题,你可以是其中任意一个矩阵,也可以两个相加的平均,或者在平均时给每一个矩阵附加一个权值。
如果你还对这两个矩阵的跟新规则还有疑问,那么下面会做一个实际的案例追踪,讲解两个矩阵的更新过程。
word2vec的整个计算过程
结合上面的介绍对整个流程做一个介绍,首先依旧是以:this cat is very cute做为例子。
1.以滑窗移动获得语料(滑窗大小我们定义为2),以cat为中心词获取样本:
this为中心词时:this cat is
cat为中心词时:this cat is very
is为中心词时:this cat is very cute
very为中心词时:cat is very cute
cute为中心词时:is very cute
当以cat为中心词时,获得正负样本
cat为中心词时:this cat is very
转换为共现概率表达
| input1 | input2 | label |
|---|---|---|
| cat | this | 1 |
| cat | is | 1 |
| cat | very | 1 |
| cat | cute | 0 |
假如举例cat this 。
首先假设:矩阵A是单词以中心词时才进行跟新,矩阵B是单词不是中心词时进行更新的。
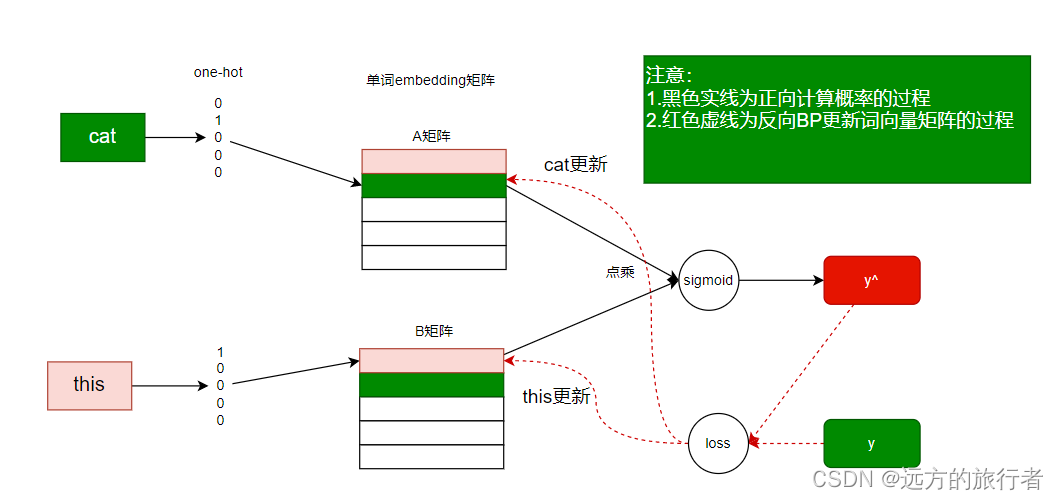
- 将this和cat进行one-hot输入到模型中。
- 根据one-hot值,到两个embedding向量矩阵中取得对应的行,也就是这两个单词对应的向量表达,但是细节在于此时的cat是去A矩阵中取得一行向量,因为此时它是中心词,而this是去B矩阵中取得一行向量。
- 将这两行向量进行相乘,得到一个数,最后对相乘得到的数进行sigmoid,得到的概率,就是以cat为中心词时,预测this的概率。
- 这时候如果预测的概率是0.42,因为这里的真实的label是1,所以就可以设定loss = y-y^ = 1-0.42,然后依据sgd等优化方法,更新A矩阵里的对应的cat的向量,那this的embedding向量需要更新吗?需要的啦,只是它是在B矩阵里更新了,为啥会这样呢?
其实理解的时候可以先不用管this,我们看cat,这时候的cat更新的是A矩阵,那何时更新B矩阵里对应的cat的向量呢?是在cat不作为中心词的时候进行更新,也就好比这里的this,这里的this就更新的是B矩阵,因为此时他不是作为中心词。但是当this作为中心词时,它就会来更新A矩阵对应位置的向量,这样两个都训练到了。
注:这里的this取的是B矩阵的向量,其实也可以取A矩阵的对应向量。
优化篇
问题提出
回顾以上的步骤讲解,有两个地方明显的会让我们的训练模型的时候有阻碍
问题1:负样本太多
问题描述:
当以cat为中心词时,thiscat is very 是滑窗内的正样本,但是如果此时语料库中有10w个单词,那除了the和is之外,其他的单词和cat的组合全部都为负样本,你想这才只是仅以cat为中心词时的负样本就这么多,全部滑窗循环下来,负样本将无比巨大
问题后果:
负样本太多,会导致训练样本失衡,同时负样本太多会导致数据量太大难以训练、以及训练模型有偏。
问题解决:
既然负样本太多,最直观的减少负样本的解决方法不就是少取一点嘛,这里提出的一个负采样,其实就是抽样的取负样本,不全部取,而是取部分,这很好理解。至于到底取多少呢?通常是正负样本按照1:10的比例来取,也就是取正样本的10倍左右的量。
问题2:softmax计算量太大
问题描述,在最开始的skip-gram的原理介绍中,每进行一次单词的共现预测时,都会涉及到一个问题:就是softmax计算, 可以回顾一下softmax的公式,你会发现每进行一次softmax计算,我们的分母上都要对全部单词的预测输出值进行计算,然后加和,显然这样的复杂度是n。虽然我们在word2vec中将softmax的多分类问题改为了共现的而二分类问题。但是可以理解为计算的复杂程度依旧是一样的。那这个问题会有什么后果呢?
问题后果:
每一次要对某一个单词做预测时,都要对全量的单词的概率做计算,其实这是一个很复杂的事情,效率会极低。
问题解决:
这里引入了霍夫曼树的原理,首先要知道霍夫曼树的原理是什么,霍夫曼数的原理就是,将权重越大的节点,越靠近根节点。下面做个例子来例句霍夫曼树的原理。
1 1 3 12 34 9 4 30 87
在构建霍夫曼树之前要对其进行排序
1 1 3 4 9 12 30 34 87
先将最小的分配到叶子节点上。
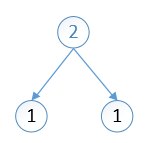
分配之后,将分配出去的节点(1,1)剔除出队列,将他们的加和(2)放入队列,然后将最小的两个拿出,进行重新排序
2 3 4 9 12 30 34 87
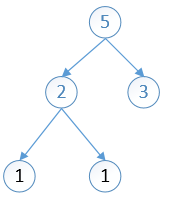
依次进行第二步的操作,将分配出去的节点(2,3)剔除出队列,将他们的加和(5)放入队列,然后重新排序,然后将最小的两个拿出
4 5 9 12 30 34 87
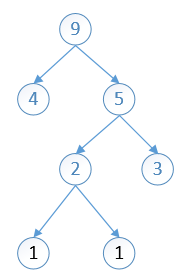
依次进行第二步的操作,将分配出去的节点(4,5)剔除出队列,将他们的加和(9)放入队列,然后重新排序,然后将最小的两个拿出
9 9 12 30 34 87
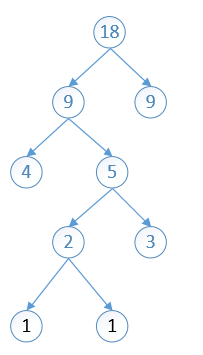
依次进行第二步的操作,将分配出去的节点(9,9)剔除出队列,将他们的加和(18)放入队列,然后重新排序,然后将最小的两个拿出
12 18 30 34 87
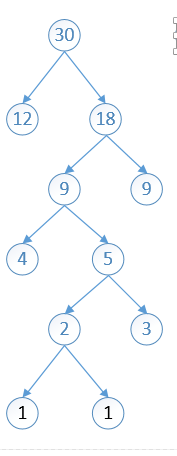
依次进行第二步的操作,将分配出去的节点(12,18)剔除出队列,将他们的加和(30)放入队列,然后重新排序,然后将最小的两个拿出
30 30 34 87
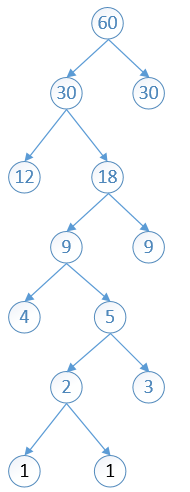
依次进行第二步的操作,将分配出去的节点(30,30)剔除出队列,将他们的加和(60)放入队列,然后重新排序,然后将最小的两个拿出
34 60 87
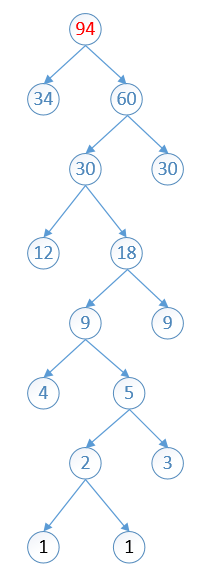
依次进行第二步的操作,将分配出去的节点(34,60)剔除出队列,将他们的加和(94)放入队列,然后重新排序,然后将最小的两个拿出
87 94
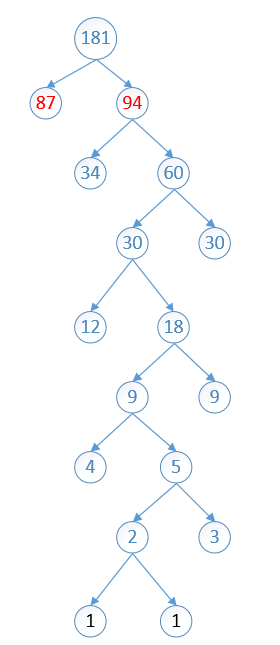
至此这棵树就构建完毕,可以发现数字最大的就会很靠近根节点(红色的),数字最小的会很原理根节点(黑色)
那为什么就可以引入这个霍夫曼树来优化我们的softmax呢(单词的共现概率的计算)?
其实就是根据每个单词出现的频率进行霍夫曼编码,首先会统计整个语料库中单词出现的次数,然后依据单词出现的次数进行霍夫曼编码(也就是将刚刚距离中的那些数字替换为具体单词出现的次数),将出现次数比较多的单词优先放到根节点附近,最终所有单词都会落到叶子节点上。
这里大家可以把softmax这个关键词忘掉,因为word2vec内部原理其实是将问题转为共现问题,本质是一个二分类的问题,所以你这里要转变为这是一个0,1的二分类的问题。
这时候还有两个个疑问:
| 疑问 |
|---|
| 1.叶子节点之外的中间节点是啥呢? |
| 2.节点之间的边又是啥呢? |
针对疑问1:我其实也不太清楚,我理解是它就是某一种规则指标,用来做每一次抉择的划分指标,所以不用太过多解读;
而针对疑问2:每一条边都是表示一个概率值,而到某一个叶子节点上要经过的路径,就是预测这个叶子节点单词的概率。
所以当我们进行单词概率预测的时候,对于高频出现的词,自然会最先找到,这就是优化本质。
举个例子,同样的引用上面的图

这里当我们将cat和is送入到模型时,如果is是在全文出现最多,那么我们在哈夫曼树中马上就会找到is,那么他的概率马上就会计算出来,所以全文中和is搭配的所有样本的概率的求解速度会非常快,求得概率之后,然后与target=1做loss,反向梯度更新权重。就完成一次训练了,这就是优化的本质。
注意:这棵树一旦构建好,结构将永远不会改变,改变的只是边的权重,也就是概率。
word2vec执行流程
下面通过举例cat来预测this的整体流程(由于原先画图的原件找不到,无法更改,下图的the就是this)
训练阶段:
1.将两个单词one-hot;
2.在矩阵A中找到cat单词和this对应的embedding向量(你也可以不在同一个矩阵中取向量)
3.将两个向量相乘得到预测概率;
4.将概率值保存到与this对应的边上;
那么在不断的训练中更新的就是这个边的权重;
预测的阶段:
1.将两个单词one-hot;
2.在矩阵A中找到两个单词的对应的embedding向量;
3.找到到this的边的权重,这个就是概率;
你想想,他们进行相乘以后,假设相乘的结果就是一个进入了一个霍夫曼树编码的根节点上,那这时候你如果是计算this出现的概率,你就只需要依据一条线去找到this,显然复杂度大大降低,同时如果this在整篇文章中出现的次数很多,它就会被编码到根节点附件,这是效率会更高,因为只需要走一两步就找到this的概率。
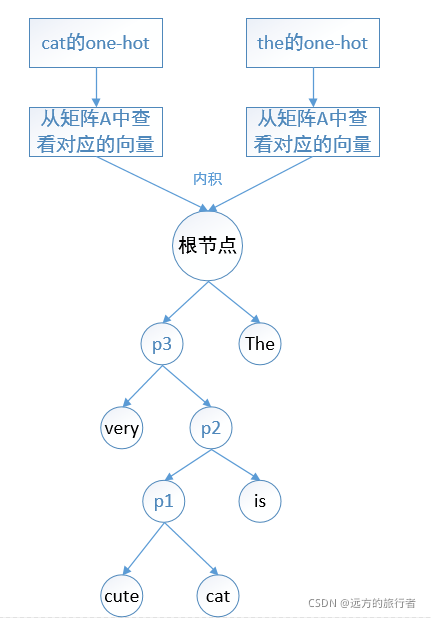
这就是对softmax的改进:层次softmax,虽然它叫层次softmax,我理解为它是对最原始的softmax上做的解释,实际的共现计算中,关于已经变成了二分类问题,而softmax中的哈夫曼编码依旧是对概率预测有优化作用,所以名字的含义可以忽略。
word2vec实现
word2vec这么有名的算法,自然已经有人实现过了,我们只需要理解原理,无需再去造轮子,本次使用的是gensim包里所支持的word2vec,调用即可。
安装gensim
pip install –upgrade gensim
- 1
文本准备(wiki_test.txt)
直接复制下来就可以用了
歐幾里得 西元前 世紀 古希臘 數學家 現在 認為 幾何 父 此畫 拉斐爾 作品 雅典 學院 数学 研究 數量 结构 变化 空间 概念 一門 学科 从 某种 角度看 屬於 形式 科學 一種 數學 利用 抽象化 邏輯推理 計數 計算 量度 物體 形狀 運動 觀察 發展 而成 數學家 拓展 概念 公式化 新 猜想 選定 公理 定義 出發 嚴謹 推導 一些 定理 數學 基本概念 完善 早 古埃及 古希臘 嚴謹 處理 數學 發展 持續 不斷 小幅 進展 世紀 文藝復興 時期 致使 數學 加速 发展 直至 今日 今日 數學 使用 一些 領域 中 包括 科學 工程 醫學 經濟學 金融學 有時 亦 激起 新 數學 發現 導致 全新 學科 發展 數學家 研究 數學 數學 实质性 內容 不以 實際 應用 目標 許多 研究 數學 过程 中 發現 許多 應用 处 詞源 西方 语言 中 數學 詞源 古希臘 語的 其有 學習 學問 科學 數學 研究 語源 形容詞 意思 學習 用功 亦 用來 指 數學 英语 中 表面 複數 形式 法语 中 表面 複數 形式 可溯 拉丁文 中性 複數 西塞罗 譯自 希臘文 複數 此一 希臘語 亚里士多德 拿來 指 萬物 皆數 概念 汉字 表示 數學 一詞 产生 于 中国 宋元 時期 多指 象數 之學 有時 含有 今天 數學 意義 秦九韶 數學 九章 永樂 大典 數書 九章 宋代 周密 所著 癸 辛雜識 記 爲 數學 數學 通軌 明代 柯尚 遷著 数学 钥 清代 杜知 耕著 數學 拾遺 清代 丁取忠 撰 直到 中國 數學 名詞 審查 委員會 研究 算學 數學 兩詞 使用 狀況 後 確認 數學 表示 今天 意義 數學 含義 历史 奇普 印加帝國 時所 使用 計數 工具 玛雅 数字 數學 有着 久遠 歷史 中國 古代 六艺 數學 一詞 西方 希腊语 詞源 mathematik ó s 意思 学问 基础 源于 m á thema 科学 知识 学问 時間 長短 抽象 數量 關係 时间 单位 日 季節 年 算術 加減乘除 自然而然 產生 歷史 曾 有過 許多 記數 系統 最初 歷史記錄 了解 數字 間 關係 測量 土地 預測 天文 事件 形成 结构 空间 时间 方面 研究 世纪 算术 微积分 概念 此時 形成 随着 數學 轉向 形式化 數學 一直 不斷 延展 科學 豐富 相互作用 發展 受惠 在歷史上 有著 許多 數學 發現 直至 今日 不斷 地有 新 發現 mikhail sevryuk 月 期刊 中 所說 數學 評論 創刊 年份 現已 超過 一百九十 萬份 每年 增加 超過 七萬 五千 份 旁邊 馬雅 數字 一個 黑點 代表 一條 黑 直線 代表 形成 純數學 應用 數學 美學 牛頓 微積分 發明者 涉及 數量 結構 空間 變化 方面 困難 問題 時 往往 拓展 數學 研究 範疇 數學 運用 見於 貿易 土地 測量 之後 天文學 今日 數學 亦 給出 許多 問題 牛頓 莱布尼兹 微積分 發明者 費曼 發明 費曼 路徑 積分 這是 推理 物理 洞察 二者 產物 今日 弦 理論 亦 引申 出新 數學 一些 數學 只 生成 領域 用來 解答 領域 問題 成為 數學 概念 最純 數學 通常 亦 實際 用途 此一 非比尋常 事實 年 諾貝爾 物理 獎得主 維格納 稱為 如同 大多數 研究 領域 主要 分歧 純數學 應用 數學 應用 數學 分成 兩大 領域 變成 學科 統計學 電腦 科學 許多 數學家 談論 數學 優美 其內 美學 及美 簡單 一般化 即為 美的 一種 亦 包括 巧妙 證明 加快 計算 數值 方法 快速 傅立葉 變換 高 德菲 哈羅德 哈代 一個 數學家 自白 符號 語言 精确性 現代 符號 中 此一 圖像 產生 x cos arccos sin 〡 arcsin cos 〡 世紀 後 發明 在此之前 數學 文字 形式 書寫 這種 形式 限制 數學 發展 初學者 卻常 對此 望而却步 壓縮 少量 符號 包含 大量 訊息 如同 音樂 符號 現今 數學 符號 明確 語法 有效 訊息 作 編碼 這是 書寫 方式 難以 做到 符号化 形式化 数学 迅速 发展 數學 語言 亦 初學者 感到 困難 亦 困惱 初學者 開放 字 數學 裡有 特別 意思 數學 術語 亦 包括 胚 可積性 專有名詞 數學 需要 日常用語 精確性 嚴謹 现实 应用 中 定理 希臘人 期許 仔細 論證 牛頓 時代 使用 法則 嚴謹 牛頓 解決問題 做 定義 今日 大量 計算 難以 驗證 時 證明 亦 很難說 足夠 嚴謹 公理 傳統 思想 中是 不證 自明 真理 這種 想法 問題 形式 公理 一串 符號 依據 哥德爾 完備 定理 意義 下 數學 科學 卡爾 弗里德里希 高斯 卡爾 弗里德里希 高斯 稱 數學 科學 皇后 拉丁 原文 德語 應於 科學 單字 意思 皆 知識 領域 實際上 科學 認為 科学 只 指 物理 世界 時 數學 至少 純數學 一門 科學 愛因斯坦 曾 描述 數學 定律 越 現實 越 確定 確定 現實 越 卡爾 波普爾 定義 科学 年代 時 波普爾 推斷 大部份 數學 定律 物理 生物學 假設 演繹 現在 接近 思想家 如較 著名 拉 卡托斯 觀點 則為 科學 領域 理論物理 公理 嘗試 符合 現實 數學 事實上 理論 物理學家 齊曼 john ziman 認為 科學 一種 公眾 知識 亦 包含 數學 情況 下 減輕 數學 使用 科學 方法 缺點 史蒂芬 沃爾夫 勒姆 年 著作 一種 新 科學 中 提出 數學家 對此 態度 並不 一致 哲學家 低估 美學 方面 重要性 創造 藝術 發現 科學 爭議 大学 院系 划分 中 常见 科学 数学系 實際上 細節 卻 分開 數學 領域 有如 反映 中國 算盤 了解 數字 間 關係 測量 土地 預測 天文 事件 四種 需要 數量 結構 空間 變化 算術 代數 幾何 分析 數學 廣泛 子 領域 相關 連著 上述 主要 關注 之外 邏輯 集合論 基礎 科學 經驗 數學 應用 數學 近代 不確定性 嚴格 研究 基礎 哲學 闡明 數學 基礎 研究 此一 架構 數學 邏輯 總是 存在 證明 真 命題 現代 邏輯 分成 遞歸論 模型 證明 千禧年 大獎 難題 中 p px px 數學 邏輯 集合論 範疇 纯粹 数学 数量 數量 研究 起於數 孿生 質數 猜想 哥德巴赫猜想 當數系 發展 時 整數 被視 有理數 子集 有理 數則 包含 實數 中 連續 量 實數 表示 實 數則 進一步 廣義 化成 複數 自然數 亦 推廣 超限 數 形式化 計數 無限 這一 概念 一個 研究 領域 大小 阿列 夫数 自然數 整數 有理數 實數 複數 結構 物件 結構 性質 探討 群 zh cn zh tw 抽象 系統 中 該些 物件 事實上 系統 此為 代數 領域 一個 重要 概念 廣義 化至 向量 空間 向量 線性代數 中 研究 數量 結構 空間 變化 纯粹 数学 研究 抽象 结构 理论 结构 布尔 巴基 学派 认为 三种 抽象 结构 代数 结构 序 结构 偏序 全序 拓扑 结构 邻域 极限 连通性 维数 px px px px 數論 群論 圖論 序 理論 空間 空間 研究 源自 幾何 尤其 欧几里得 几何 三角學 結合 空間 及數 包含 著名 勾股定理 非 歐幾里得 幾何 拓撲學 數和 空間 解析幾何 結合 了數 空間 概念 亦 拓撲 群 研究 結合 結構 空間 李群 用來 研究 空間 結構 變化 許多 分支 中 包含 存在 已久 龐加萊 猜想 爭議 四色 定理 龐加萊 猜想 已 年 确认 俄罗斯 数学家 格里 戈里 佩雷尔曼 證明 四色 定理 已 年 由凱 尼斯 阿佩爾 沃夫岡 哈肯 電腦 證明 人力 驗證 px px px px px px 幾何 三角學 微分 幾何 拓撲學 碎形 測度論 變化 微積分 研究 變化 有利 工具 函數 诞生 於此 做 描述 變化 量 核心 概念 複分析 則為 複數 等價 領域 黎曼 猜想 數學 最 未決 問題 便是 複分析 描述 泛函 分析 注重 函數 無限 維 空間 這在 微分方程 中 研究 px px px px px px 微積分 向量分析 微分方程 動力系統 混沌 理論 複分析 離散數學 包含 計算 理論 計算 複雜性 理論 資訊 理論 包含 現知 最 有力 模型 圖靈機 電腦 硬體 快速 進步 最後 壓縮 熵 概念 相對 新 領域 離散數學 許多 未解 問題 最 有名 p np 問題 千禧年 大獎 難題 相信 問題 解答 否定 px px px 組合 數學 計算 理論 密碼學 圖論 應用 數學 工商業 領域 現實 問題 應用 數學 中 重要 領域 統計學 分析 預測 大部份 實驗 比較 覺得 合作 團體 一份 子 數值 分析 研究 計算方法 file gravitation space source png 數學 物理
- 1
算法训练逻辑
from gensim.models import word2vec
if __name__ == "__main__":
sentences = word2vec.LineSentence("wiki_test.txt")
model = word2vec.Word2Vec(sentences, vector_size=250)
#保存模型,供日後使用
model.save("word2vec.model")
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
word2vec.Word2Vec的参数介绍
class Word2Vec(utils.SaveLoad):
def __init__(
self, sentences=None, corpus_file=None, vector_size=100, alpha=0.025, window=5, min_count=5,
max_vocab_size=None, sample=1e-3, seed=1, workers=3, min_alpha=0.0001,
sg=0, hs=0, negative=5, ns_exponent=0.75, cbow_mean=1, hashfxn=hash, epochs=5, null_word=0,
trim_rule=None, sorted_vocab=1, batch_words=MAX_WORDS_IN_BATCH, compute_loss=False, callbacks=(),
comment=None, max_final_vocab=None, shrink_windows=True,
):
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
不全部介绍,只挑几个常用的介绍
sentences:可以是一个list,对于大语料集,建议使用BrownCorpus,Text8Corpus或lineSentence构建
vector_size:是指词向量的维度,默认为100,依据词库的大小而实际改变
window:滑窗大小,最开始我们本文举例的滑窗大小是2
alpha: 初始学习速率
min_count: 需要计算词向量的最小词频
negative:即使用Negative Sampling时负采样的个数,默认是5。推荐在[3,10]之间
sample: 高频词汇的随机降采样的配置阈值,默认为1e-3,范围是(0,1e-5)
workers:用于控制训练的并行数
其他的参数含义可以参考源码,源码有很详细的解释。
测试
# -*- coding: utf-8 -*- from gensim.models import word2vec from gensim import models import logging def main(): logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO) model = models.Word2Vec.load('word2vec.model') print("提供 3 種測試模式\n") print("輸入一個詞,則去尋找前一百個該詞的相似詞") print("輸入兩個詞,則去計算兩個詞的餘弦相似度") print("輸入三個詞,進行類比推理") while True: try: query = input() q_list = query.split() if len(q_list) == 1: print("相似詞前 100 排序") res = model.wv.most_similar(q_list[0],topn = 100) for item in res: print(item[0]+","+str(item[1])) elif len(q_list) == 2: print("計算 Cosine 相似度") res = model.wv.similarity(q_list[0],q_list[1]) print(res) else: print("%s之於%s,如%s之於" % (q_list[0],q_list[2],q_list[1])) res = model.wv.most_similar([q_list[0],q_list[1]], [q_list[2]], topn= 100) for item in res: print(item[0]+","+str(item[1])) print("----------------------------") except Exception as e: print(repr(e)) if __name__ == "__main__": main()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
结果输出:
提供 3 種測試模式 輸入一個詞,則去尋找前一百個該詞的相似詞 輸入兩個詞,則去計算兩個詞的餘弦相似度 輸入三個詞,進行類比推理 今日 相似詞前 100 排序 變化,0.45874717831611633 中,0.39984795451164246 空間,0.35042184591293335 發現,0.3165726363658905 科學,0.2881494164466858 px,0.2769666314125061 幾何,0.20821087062358856 複數,0.20188158750534058 數學家,0.1428254097700119 發展,0.14026466012001038 應用,0.1364540457725525
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
至此关于优化的也记录完毕,可能我理解的不是很对。今次作为自我记录吧,后续有更深刻的理解再回来更改。



