从前慢现在也慢

这个屌丝很懒，什么也没留下！

热门标签

知识图谱：基于嵌入的模型（TransE 、TransH、TransR和TransD）_基于transe构建多关系知识图谱模型

作者：从前慢现在也慢 | 2024-05-07 13:53:41

踩

基于transe构建多关系知识图谱模型

（一）TransE: Translating Embeddings for Modeling Multi-relational Data. Antoine Bordes, Nicolas Usunier, Alberto Garcia-Duran, Jason Weston, Oksana Yakhnenko. NIPS 2013.

论文地址：http://papers.nips.cc/paper/5071-translating-embeddings-for-modeling-multi-relational-data.pdf

代码地址：https://github.com/thunlp/OpenKE

一、引言

表示学习是深度学习的热门方向，自从word embedding出现后，关于知识图谱中结构化信息的三元组的表示学习研究也开始进入大家视野。

论文考虑了关于多元关系数据的实体和关系嵌入到低维度向量空间的问题。论文的目标是提出一个容易训练的简易模型，包括降低参数数量，且可以适用大规模数据集。并基于此，论文提出了TransE方法，可以将对关系的建模在低维度的实体表征空间上视为一种翻译操作。尽管这样很简单，这种假设证明是有效的，在两个知识库上的链接预测广泛的实验表明TransE模型超越了最佳模型。模型的损失函数是基于实体和关系向量的计算。另外，它还可以成功的在大规模数据集上进行训练，包括1M个实体，25k个关系，超过17m个训练样本。

Multi-relational data（多元关系数据）是指有向图中包括头实体h 、尾实体t以及两者之间的关系类l ，表示为三元组 $(h,l,t)$ 。以这种三元组结构的任务有社交网络（social network）、推荐系统（recommender systems）、知识库（knowledge bases）。论文的任务是聚焦于对知识库（WordNet、FreeBase）中多元关系数据进行建模，同时提供一种高效的工具用于知识补全，不需要额外的知识。

（1）构建多元数据。通常关系数据包括单一关系数据（single-relational data）和多元关系数据（multi-relational data）。单一关系通常是结构化的，可以直接进行简单的推理；多元关系则依赖于多种类型的实体和关系，因此需要一种通用的方法能够同时考虑异构关系。

（2）关系可以作为嵌入空间之间的翻译。论文提出一种基于能量机制的模型来训练低维度实体嵌入，TransE认为，如果实体对存在，则头实体与之对应的关系向量之和和尾实体尽可能相同。即 $h+l\approx t$ 。

二、伪代码和目标函数构建

TransE伪代码

上述1~3步，对实体E和关系L进行初始化，但是实体没有除以L2范数归一化。

4~13为循环步骤，第5步中，对实体e进行L2范数归一化；采样一个大小为b的batch，记为 $S_{batch}$ ；初始化储存三元组对的列表；8~11为内循环，对 $S_{batch}$ 中的每个正样本替换头实体 $h$ 或者尾实体 $t$ 构造负样本，然后把对应的正样本三元组和负样本三元组放到一起，组成 $T_{batch}$ ，本质上是完成正负样本的提取；第12步，梯度下降训练目标函数。

对于给定的训练集 $S$ ，三元组表示为 $(h,l,t)$ ，其中 $h,t$ ∈ 实体集 $E$ ， $l$ ∈ 关系集 $L$ ，实体和关系的嵌入维度设为 $k$ ，我们希望 $h+l$ 与 $t$ 能够尽可能的“相似”，因此定义一个能量函数：

$d(h+l,t)=[(h+l)-t]^{2}$

可知这是一个单纯的欧氏距离，即两个目标向量对应坐标距离。

为了训练实体对嵌入和关系嵌入，需要引入负样本。因此我们的目标是尽可能对正样本中最小化 $d(h+l,t)$ ，负样本中则尽可能最大化 $d(h{}'+l,t{}')$ ，其中 $h{}',t{}'$ 表示不属于某个三元组的实体。，因此可以得出基于间距排序标准目标优化函数：

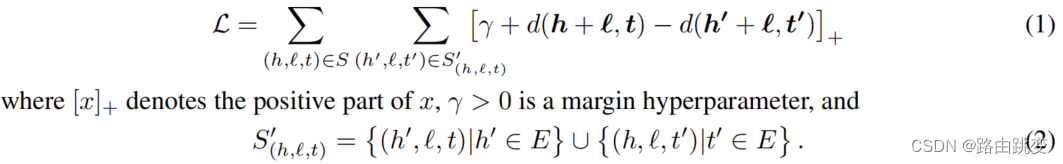
目标优化函数

三、实验分析

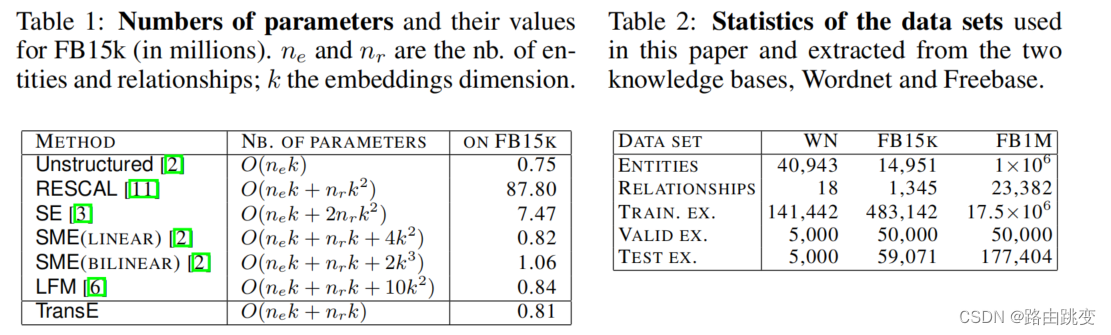
参数量与数据集信息

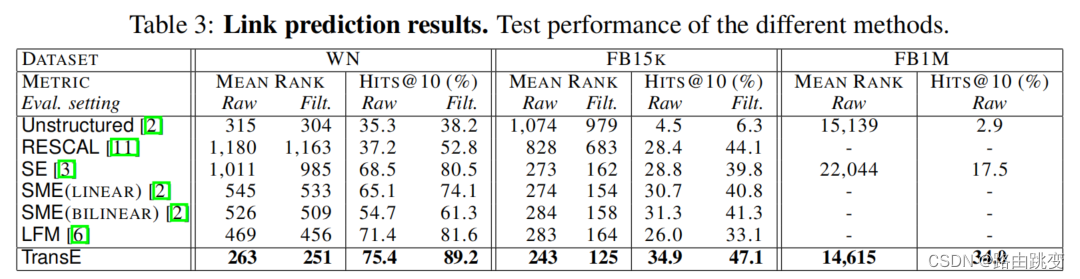
链路预测结果

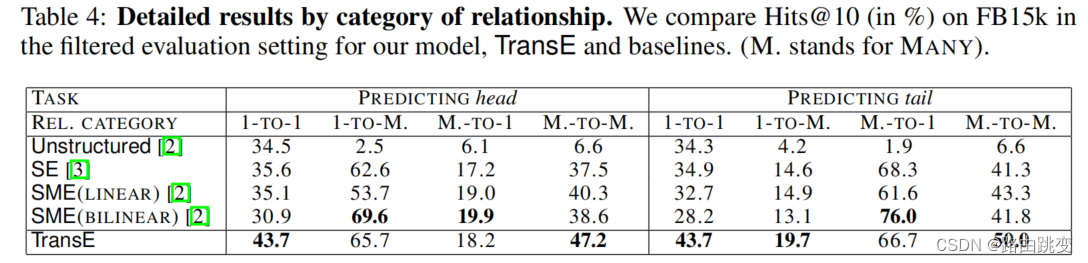
更细致划分的实验结果

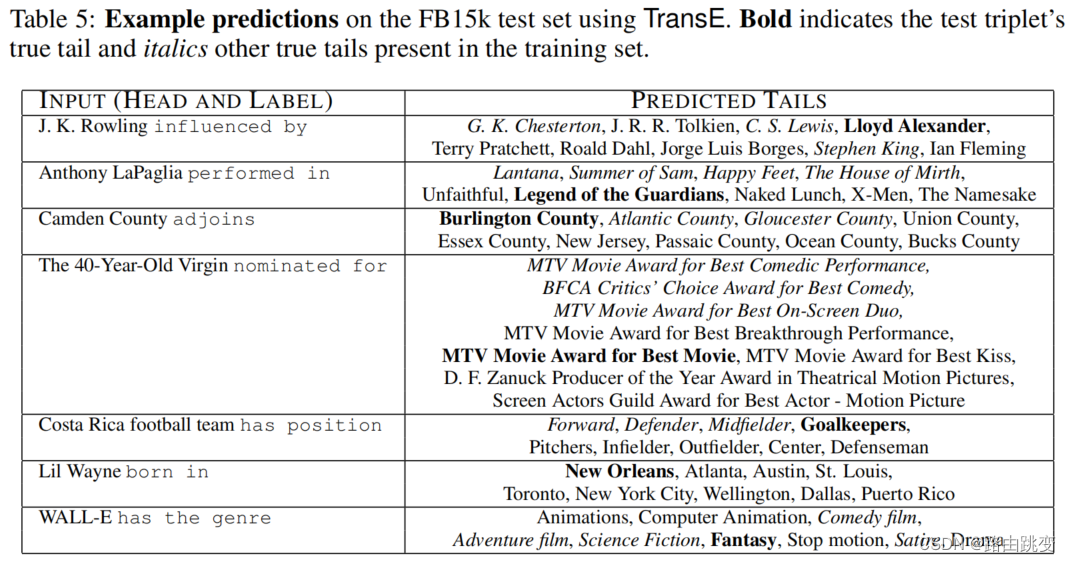
根据头实体和关系预测尾实体

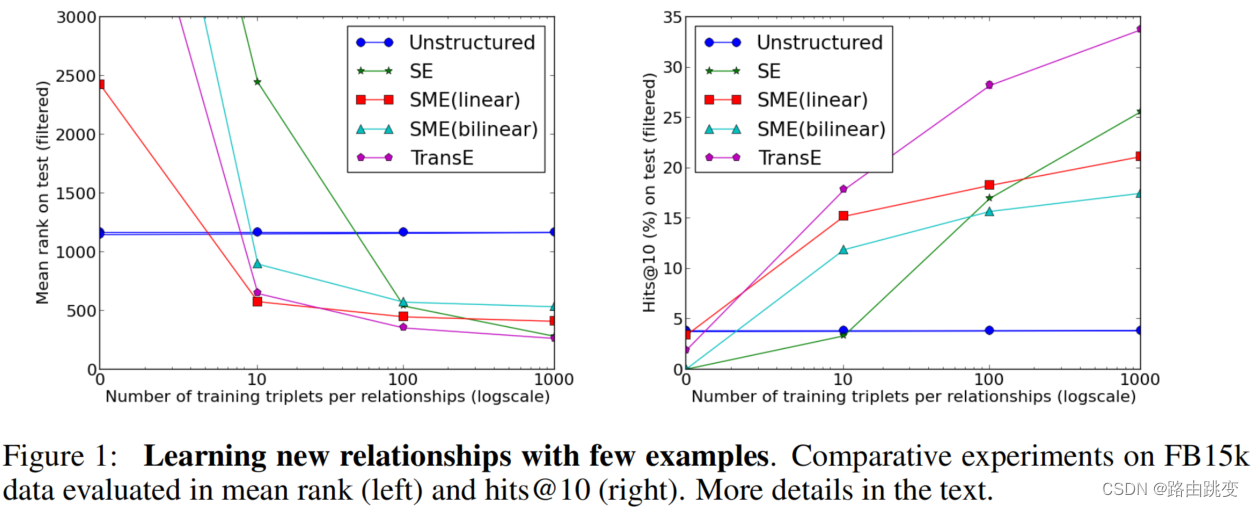
根据少量样本学习新关系

四、结论

作为Trans系列论文的开山之作，本文提出一种新的学习知识库的表示嵌入的方法，并且在不同的知识库上的实验展示了这项工作与其他方法相比具有参数量少、可应用规模更大、更高效等优点。

但模型也存在着缺点，模型过于简单导致不能很好的学习到复杂的网络语义关系，这也是后续Trans系列论文的改善方向之一，如TransH。

（二）TransH: Knowledge Graph Embedding by Translating on Hyperplanes. Zhen Wang, Jianwen Zhang, Jianlin Feng, Zheng Chen. AAAI 2014.

论文地址：https://www.aaai.org/ocs/index.php/AAAI/AAAI14/paper/viewFile/8531/8546

代码地址：https://github.com/thunlp/OpenkE

一、研究问题

知识图谱表示学习，可用于知识推理和补全技术，论文主要研究如何更好地学习到由实体和关系组成的大规模知识图谱在低维连续向量空间的嵌入向量（embedding）。知识图谱一般由结构化的RDF三元组来表示——（头实体，关系，尾实体），如（美国，总统，奥巴马）表示为美国的总统为奥巴马，在图数据结构上表示为两个实体节点，分别为美国和奥巴马，它们由一条名为总统的无向边相连接。

论文提出的模型希望可以将结构化的三元组信息输入经过表示学习方法，输出学习到的关于整个知识图谱信息的低维连续嵌入向量，这些嵌入向量能够能够轻易应用到下游的特定机器学习任务中，例如链路预测，这项技术能够应用于知识推理和补全技术中，使知识图谱更完整、更丰富。

二、论文动机

TransE是当时已提出模型中效果最好、最有前景的模型，取得了SOTA的表现。但是TransE存在着自身的局限，其在处理自反关系以及一对多、多对一、多对多关系时存在天然的不足：

由之前（一）中写过的TransE可以知道，TransE算法的核心思想是对于一个三元组 $(h,r,t)$ ∈Δ（ Δ 表示正确的三元组集合 ; Δ′ 表示不正确的三元组集合，所以 $(h,r,t)$ ∈Δ表示这个三元组 $(h,r,t)$ 是正确的），那么应该有 $h+r=d$ ，于是可以从TransE模型中得到两个结论:

（1）如果 $(h,r,t)$ ∈Δ 并且 $(t,r,h)$ ∈Δ ，表面关系 $r$ 是一个自反映射，此时按公式， $r=0$ 以及 $h=t$ 。

（2）若 $\forall i\in \left \{ 0,1,2,...,m-1 \right \}$ $(h_{i},r,t)$ ∈Δ ，表明关系 $r$ 是一个多对一的映射关系，并且 $h_{0}=h_{1}=...=h_{m}$ ；类似地，如果 $\forall i\in \left \{ 0,1,2,...,m-1 \right \}$ , $(h,r,t_{i})$ ∈Δ ，则说明关系 $r$ 是一个一对多的映射关系，并且 $t_{0}=t_{1}=...=t_{m}$ 。

以上述第二点为例子，具体地假如知识图谱中存在两个三元组（美国，总统，川普）和（美国，总统，奥巴马），这里的“总统”关系显然是一对多的映射关系，如果按TransE的方法，则学习到的“川普”和“奥巴马”的向量是一样的，这显然是不符合事实的，因为他们是完全不一样的人。类似地，对于自反映射关系也是，TransE会使得头尾两个实体的嵌入向量一样，不合实际。

因此，上述TransE的局限性影响了它的效率以及发展，而对于其他可以很好区分这些映射关系的复杂模型却牺牲了效率，总体效果不如TransE。因此论文作者希望提出一个综合的模型，这个模型既能解决上述局限性问题又能使得模型的复杂度接近TransE而有着高性能的表现。

三、方法设计

1. 解决方法

为了解决TransE在面对自反关系以及多对一、一对多、多对多关系的不足，论文提出让一个实体在不同的关系下拥有不同的表示，论文所提模型为每一个关系定义一个超平面 $W_{r}$ 以及在超平面 $W_{r}$ 上定义关系向量 $d_{r}$ 。假设 $h_{\perp }$ , $t_{\perp }$ 是 $h,t$ 在超平面 $W_{r}$ 上的投影，则此时正确的三元组应该满足 $h_{\perp }$ + $d_{r}$ = $t_{\perp }$ ，这样能够使得同一个实体在不同关系中的表示不同，同时不同实体在同一个关系中的表示也不同。我们可以从数学几何角度来看待这个对原始TransE的改动，如下图：

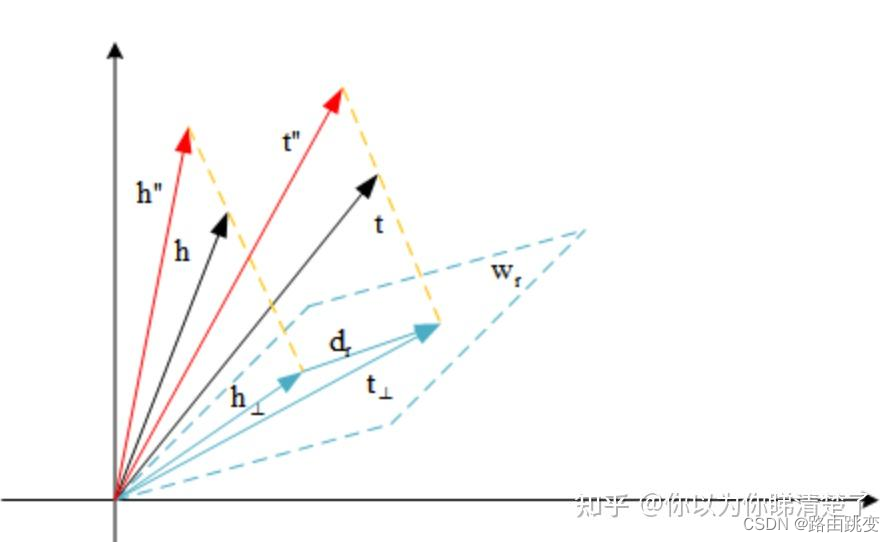
几何意义

我们可以从几何意义图例直观地感受到为什么TransH可以克服TransE的局限性，对上述图例，显然有 $(h,r,t)$ ∈Δ 以及 $(h{}'',r,t)$ ∈Δ ，这是一种多对一的情况，如果在TransE中，有 $h=h{}''$ ，但显然我们的图上 $h\neq h{}''$ ，因此TransH的方法使得 ， $h,h{}''$ 在超平面 $W_{r}$ 上的投影相同即可表示这种多对一的关系，类似地，其他关系同理，这样就能有效从向量上区分 $h,h{}''$ ，提高模型的准确率。

2. 损失函数

同时，由于一个关系 $r$ 可能存在无限个超平面，因此论文作了约束条件，令 $w_{r}$ 为超平面 $W_{r}$ 的法向量，令 $\left \| w_{r} \right \|_{2=1}$ ，并且我们可以轻易得出Scoring function为 $\left \| h_{\perp }+d_{r}-t_{\perp } \right \|_{2}^{2}$ ，由此可以轻易得到：

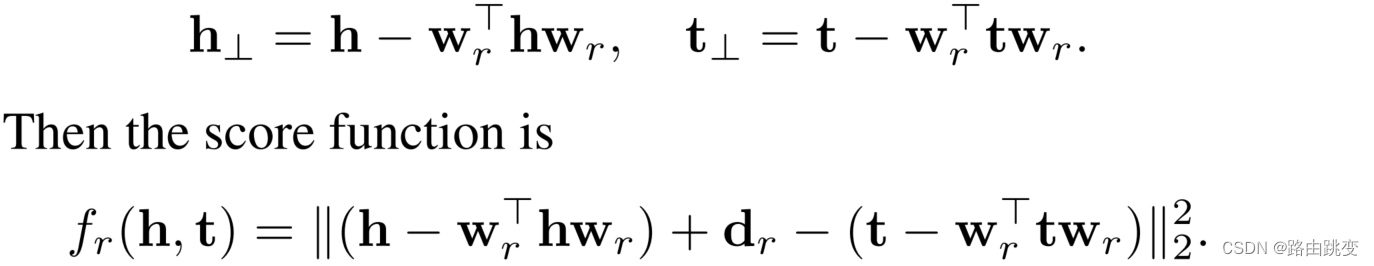
Score Function

最后，论文考虑了一系列的优化损失函数的约束条件，如下图：

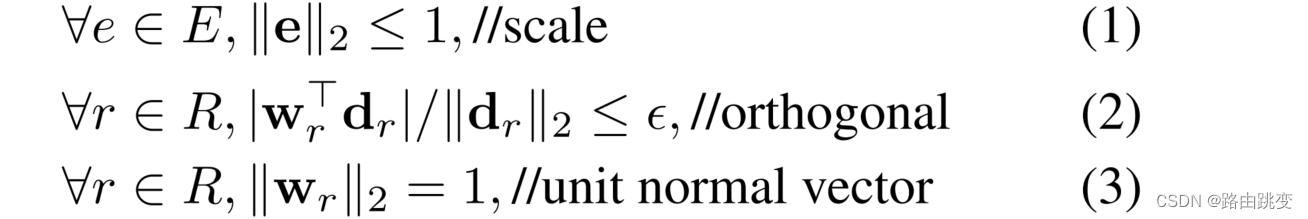
约束条件

约束条件（2）确保向量 $d_{r}$ 在超平面里，论文没有直接去优化该损失函数，而是通过软约束的方法将其转变为无约束损失函数：

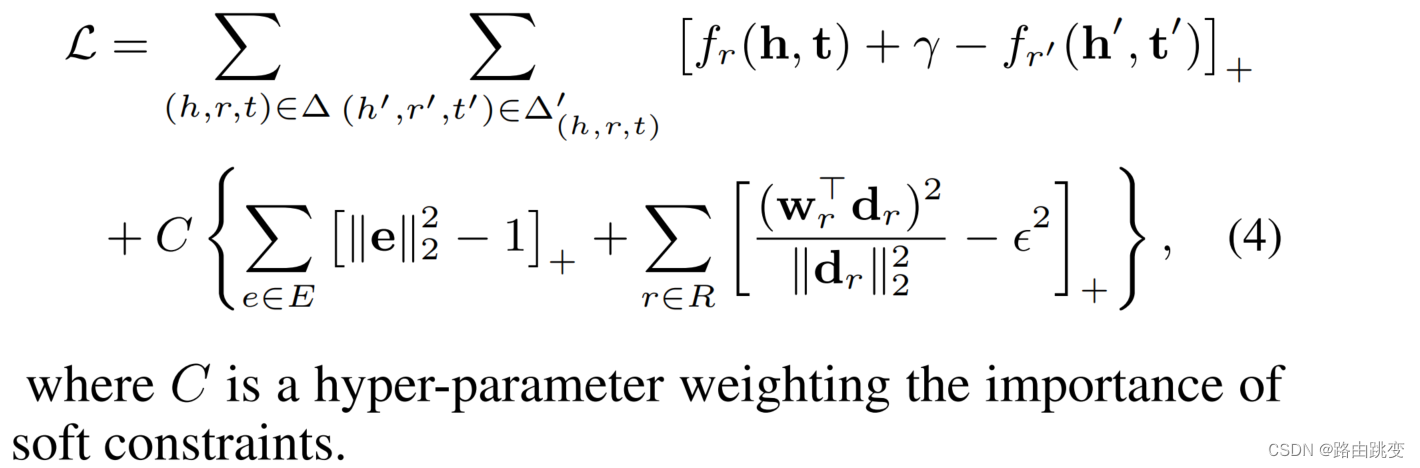
最终损失函数

3. Trick：减少错误的负标签

对于先前TransE的负采样方法，只是简单地随机替换正确三元组的头实体或者尾实体，但是，真实的知识图谱往往由于知识图谱构建过程的不可避免的因素而信息残缺，因此原来的采样方式可能会引入很多错误的负标签到模型训练中。

因此论文提出了一种新的作者认为更科学的负采样方法，采取不同的概率，有偏向地选择替换头实体和尾实体。例如，对于一对多的关系，论文会相对以更大概率去替换头实体；反之，如果是多

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/549574

​知识图谱：基于嵌入的模型（TransE 、TransH、TransR和TransD）_基于transe构建多关系知识图谱模型