- 1E/HiView.HiEvent: length is 0 or exceed MAX: 1024
- 2大数据毕业设计 服务器数据分析与可视化系统 - python flask_python flash 大数据展示
- 3【深度学习】L1正则化和L2正则化
- 4Linux安全审计 auditd 服务_kauditd
- 5阿里云ECS服务器退订_阿里云 退订数据盘
- 6npm install时报npm ERR! code 1npm ERR! path D:SSO\easy-backend-ui\node_modules\node-sass
- 72023年高级工程师评审条件_2023年北京市高级工程师职称评审
- 8【教程】微信小程序如何拍摄图片及视频并上传到后台进行存储_微信小程序上传视频
- 9QT With OpenGL(Texture篇)
- 10Android The application could not be installed_installation failed suggested action:
【文献阅读笔记】KAM Theory Meets Statistical Learning Theory: Hamiltonian Neural Networks with Non-Zero Trai
赞
踩
文章发表于【2022】AAAI Technical Track on Machine Learning I
文章目的
这篇文章,通过结合统计学习理论和 Kolmogorov-Arnold-Moser (KAM) 理论,为哈密顿神经网络提供在学习误差不完全为零时的行为的理论分析。
–
一、主要内容:
1.用统计学习理论证明哈密顿神经网络的训练模型是原系统的扰动
即
d
u
d
t
=
S
∂
H
N
N
∂
u
.
\frac{du}{dt} =S\frac{\partial H_{NN}}{\partial u}.
dtdu=S∂u∂HNN.
被视为扰动的哈密顿系统。
2.应用KAM理论得出神经网络学习误差行为。

二、第一部分任务:证训练系统是扰动
2. 1. 主要概念Rademacher complexity&Covering number
Rademacher complexity:一定概率下损失函数期望的界限
covering number:用于估计Rademacher complexity的界。
2. 2. 定义理解:Rademacher complexity



2. 2. 1. 引理1:用Rademacher complexity估计损失函数



因此得到引理1

2. 3. 定义理解:Covering number


2. 3. 1 引理2:用Covering number估计Rademacher complexity
引理2证明
上述定理得到原文的lemma2
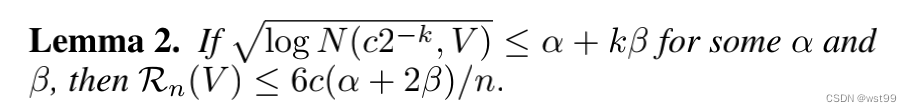
2. 4. 引理3: 给Covering number一个估计
证明


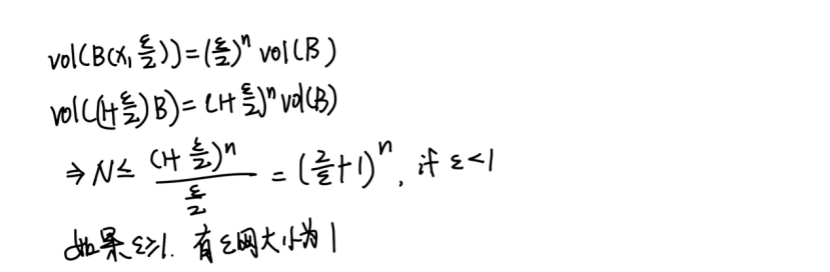
2. 4. 得出结论引理5:
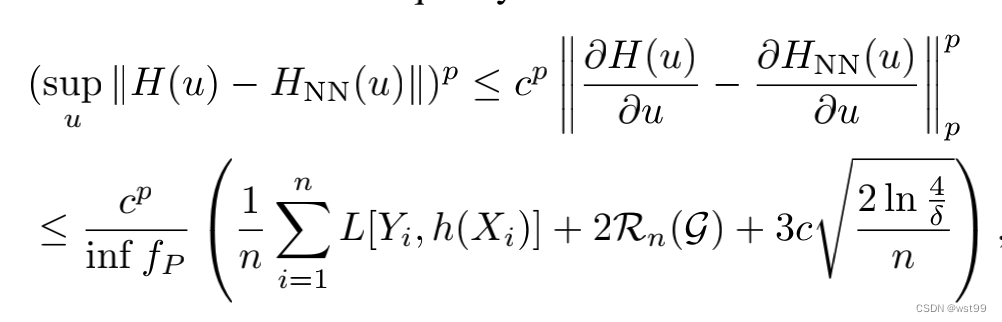
第一部分:损失函数的平均值,训练时是让损失函数不断变小
第二部分:Rademacher complexity用Covering number估计,Covering number由定理7估计。
即满足定理3的条件
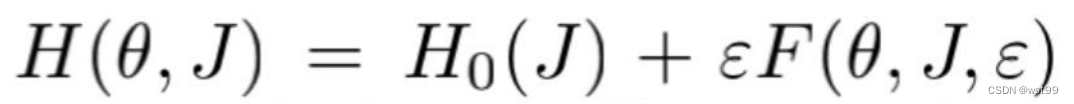
二、第二部分任务:应用KAM得出神经网络学习误差行为。
套用定理3,得出结论。


