- 1Llama-3的安装和使用方法和案例应用_llama3 怎么使用
- 2C# 第三方 UI 库_c# ui
- 3【uniapp小程序】配置tabbar底部导航栏_uniapp底部导航栏_uniapp tabbar
- 4初识FFmpeg_ffmpeg 图片名通配符
- 5探索智能应用的基石:多模态大模型赋能文档图像处理_大模型 文档智能
- 6在x86环境用vscode替代qt creator_vscode和qtcreator
- 7临床前药物研发,AI搞出来的已经占一半了? | 对撞派 · 圆桌实录
- 8产品经理-需求分析(三)
- 9双人成行UE4-nuts game已崩溃怎么解决?双人成行UE4-nuts game崩溃原因及解决方法分享_ue4-nuts game已崩溃 即将关闭
- 10JavaWeb - HTTP状态码_java http状态码实体类
【机器学习算法笔记系列】决策树(Decision Tree)算法详解和实战_decisiontreeclassifier是什么算法
赞
踩
决策树(Decision Tree)算法
算法概述
本文主要介绍机器学习中的决策树模型。决策树模型是一类算法的集合,在数据挖掘十大算法中,具体的决策树算法占有两席位置,即C4.5和CART算法。决策树是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法。决策树分为分类树和回归树两种,分类树对离散变量做决策树,回归树对连续变量做决策树。同时也特别适合集成学习比如随机森林。
一棵决策树的生成过程主要分为以下3个部分:
-
特征选择: 是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准,如何选择特征有着很多不同量化评估标准标准,从而衍生出不同的决策树算法。
-
决策树生成: 根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则停止决策树停止生长。 树结构来说,递归结构是最容易理解的方式。
-
决策树剪枝: 决策树容易过拟合,一般来需要剪枝,缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。
算法原理
决策树(Decision Tree),又称判断树,它是一种以树形数据结构来展示决策规则和分类结果的模型,作为一种归纳学习算法,其重点是将看似无序、杂乱的已知实例,通过某种技术手段将它们转化成可以预测未知实例的树状模型,每一条从根结点(对最终分类结果贡献最大的属性)到叶子结点(最终分类结果)的路径都代表一条决策的规则。
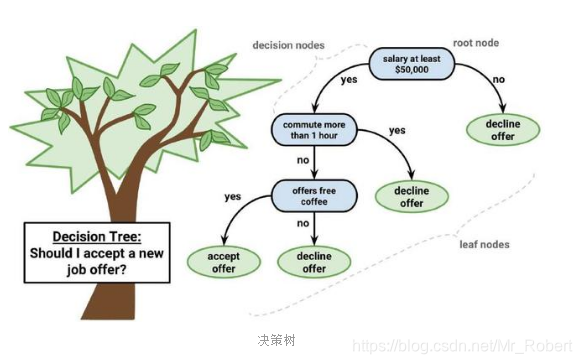
基于信息论的三种决策树算法
划分数据集的最大原则是:使无序的数据变的有序。 如果一个训练数据中有20个特征,那么选取哪个做划分依据?这就必须采用量化的方法来判断,量化划分方法有多重,其中一项就是“信息论度量信息分类”。基于信息论的决策树算法有ID3 、C4.5和 CART等算法,其中C4.5和CART两种算法从ID3算法中衍生而来。
ID3算法
ID3算法使用 信息增益 作为分裂的规则,信息增益越大,则选取该分裂规则。多分叉树。信息增益可以理解为,有了x以后对于标签p的不确定性的减少,减少的越多越好,即信息增益越大越好。
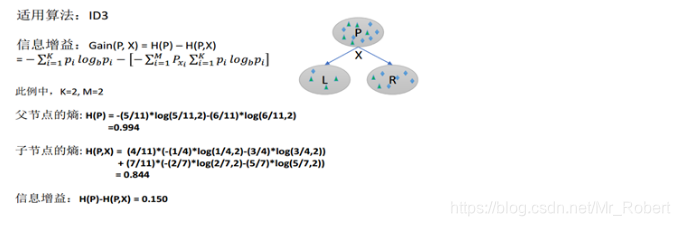
ID3算法可用于划分标称型数据集,没有剪枝的过程,为了去除过度数据匹配的问题,可通过裁剪合并相邻的无法产生大量信息增益的叶子节点(例如设置信息增益阀值)。使用信息增益选择属性,其实是有一个缺点,那就是它偏向于具有大量值的属性——就是说在训练集中,某个属性所取的不同值的个数越多,那么越有可能拿它来作为分裂属性,而这样做有时候是没有意义的,另外ID3不能处理连续分布的数据特征,于是就有了C4.5算法。CART算法也支持连续分布的数据特征。
C4.5算法
C4.5算法是ID3的一个改进算法,继承了ID3算法的优点。使用信息增益率作为分裂规则(需要用信息增益除以,该属性本身的熵),此方法避免了ID3算法中的归纳偏置问题,因为ID3算法会偏向于选择类别较多的属性(形成分支较多会导致信息增益大)。多分叉树。连续属性的分裂只能二分裂,离散属性的分裂可以多分裂,比较分裂前后信息增益率,选取信息增益率最大的。
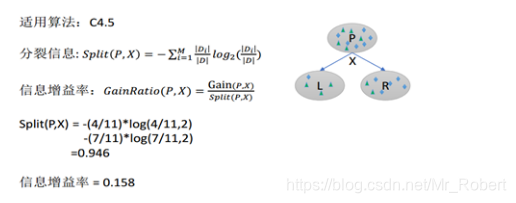
C4.5算法用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足,在树构造过程中进行剪枝;能够完成对连续属性的离散化处理;能够对不完整数据进行处理。C4.5算法产生的分类规则易于理解、准确率较高;但效率低,因树构造过程中,需要对数据集进行多次的顺序扫描和排序。也是因为必须多次数据集扫描,C4.5只适合于能够驻留于内存的数据集。
CART算法
CART的全称为Classification And Regression Tree,即分类回归树(只能形成二叉树)。采用的是Gini指数(选Gini指数最小的特征s)作为分裂标准,同时它也是包含后剪枝操作。ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但其生成的决策树分支较大,规模较大。为了简化决策树的规模,提高生成决策树的效率,就出现了根据GINI系数来选择测试属性的决策树算法CART。
对于分类树(目标变量为离散变量):使用基尼系数作为分裂规则。比较分裂前的gini和分裂后的gini减少多少,减少的越多,则选取该分裂规则,这里的求解方法只能是离散穷举。关于基尼系数,可以参考周志华的西瓜书决策树那章,讲得比较简洁,也比较易懂。“直观来说,(数据集D的基尼系数)Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小,则数据集D的纯度越高。”
具体这个的计算,我觉得有例子才好理解,下面这个红绿球的例子很好的说明了,如何根据损失函数最小(也就是基尼系数最小)来选取分裂规则。

对于回归树(目标变量为连续变量):使用最小方差作为分裂规则。只能生成二叉树。

算法优缺点
优点
- 不需要任何领域知识和参数假设。
- 决策树算法易于理解和实现,树的结构可以可视化出来 。
- 能够同时处理数据型和常规线数据,对缺失值不敏感。
- 可以处理多维度输出的分类问题。
- 效率高:决策树只需要构建一次,反复使用,每一次预测的最大计算次数不超过决策树的深度。
缺点
- 对于各类别样本数量不一致的数据, 信息增益的结果偏向于那些更多数值的特征。
- 当类别太多时,容易出现“过拟合”问题。
- 忽略数据集中属性之间的相关性,在处理特征关联性比较强的数据时表现不是很好。
- 不支持在线学习。
- 决策树可能是不稳定的,因为数据中的微小变化可能会导致完全不同的树生成。可以通过决策树的集成来缓解。
Python实践
决策树算法既可用于解决分类问题,也可以用于解决回归问题。scikit-learn中提供了一个DecisionTreeRegressor实现回归决策树,用于回归问题:DecisionTreeRegressor;提供了一个DecisionTreeClassifier实现分类决策树,用于分类问题。这里,我们主要讲分类决策树:DecisionTreeClassifier 。
其原型为:sklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)
参数
criterion:str,指定切分质量的评价标准。
gini:表示切分时评价准则是Gini系数。entropy:表示切分时评价标准是熵。
splitter:str,指定切分原则。
best:表示选择最优的切分。random: 表示随机切分。
max_depth:int或者None,指定树的最大深度。
min_samples_split:int,指定每个内部节点(非叶节点)包含的最少的样本数。
min_samples_leaf:int,指定每个叶节点包含的最少的样本数。
min_weight_fraction_leaf:float,叶节点中样本的最小权重系数。
max_features:str、float、int或者None,指定寻找best split时考虑的特征数量。
- 如果是
int,则每次切分只考虑max_features个特征。 - 如果是
float,则每次切分只考虑max_features*n_feature个特征(max_features指定了百分比)。 - 如果是字符串
auto或者sqrt,则max_features等于sqrt(n_features)。 - 如果是字符串
log2,则max_features等于log2(n_features)。 - 如果是
None,则max_features等于n_features。
random_state:int、RandomState实例,或者为None。
- 如果为
int:指定随机数生成器的种子。 - 如果为
RandomState实例:指定随机数生成器。 - 如果为
None:使用默认的随机数生成器。
max_leaf_nodes:int或者None,指定最大的叶节点数量。如果为None,此时叶节点数量不限;如果非None,则max_depth被忽略。
class_weight:字典、字典的列表,字符串balanced或者None,指定分类的权重。权重的形式为:{class_label: weight}
- 如果为字符串
balanced:则每个分类的权重与该分类在样本集中出现的概率成反比。 - 如果未指定:每个分类的权重都为1。
presort:bool,指定是否要提前排序数据,从而加速寻找最优切分的过程。设置为True,对于大数据集会减慢总体的训练过程;但是对于一个小数据集或者设定最大深度的情况下,会加速训练过程。
属性
classes_: 分类的标签值。
feature_importances_: 给出特征的重要程度。该值越高,说明该特征越重要(也称为Gini importance)。
max_features_: max_features的推断值。
n_classes_: 给出分类的数量。
n_features_: 执行fit之后,特征的数量。
n_outputs_:执行fit之后,输出的数量。
tree_:一个Tree对象,即底层的决策树。
方法
fit(X, y[, sample_weight, check_input, ...]): 训练模型。
predict(X[, check_input]): 用模型进行预测,返回预测值。
predict_log_proba(X): 返回一个数组,数据的元素依次是X预测为各个类别的概率的对数值。
predict_proba(X): 返回一个数组,数组的元素依次是X预测为各个类别的概率值。
score(X, y[, sample_weight]): 返回在(X, y)上预测的准确率(accuracy)。
决策树算法实战—预测泰坦尼克幸存者
本文使用决策树算法,对泰坦尼克号上哪些人可能成为幸存者进行预测,数据来源于Kaggle,泰坦尼克数据地址。
我们先下载csv文件,然后利用pandas加载这些数据,train.csv是一个892行,12列的数据。意
__author__ = "fpZRobert" """ 决策树算法—泰坦尼克幸存者预测 """ import pandas as pd import warnings warnings.filterwarnings('ignore') """ 加载数据 """ # 加载训练集 train_data = pd.read_csv('./data/train.csv') # 查看数据形状 print("train_data.shape: ", train_data.shape) # (981, 12) print(train_data.head()) # 查看数据前5行
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18

| 特征 | 含义 |
|---|---|
| PassengerID | 乘客的ID号,用来唯一标识乘客。 |
| Survived | 1表示幸存,0表示遇难,这是类别 |
| Pclass | 仓位等级 |
| Name | 乘客名字 |
| Sex | 乘客性别 |
| Age | 乘客年龄 |
| SibSp | 兄弟姐妹同在船上的数量 |
| Parch | 同船的父辈人员数量 |
| Ticket | 乘客票号 |
| Fare | 乘客的体热特征 |
| Cabin | 乘客所在的船舱号 |
| Embarked | 乘客登船的港口 |
我们先查看一下数据信息总览,然后我们需要先分析这些特征,以便决定哪些特征可以用来进行模型训练:
# 数据信息总览
print(train_data.info())
- 1
- 2
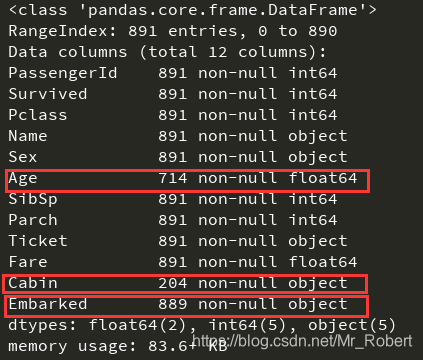
首先,我们发现PassengerID、Name、Ticket这三个特征只做标识乘客的作用,与是否幸存无关,所以我们去掉这两个特征。另外,通过输出数据信息可知,age、Cabin、Embarked均存在缺失值的情况,尤其是Cabin,缺失了大部分信息,所以我们暂且先丢弃这个特征。Embarked是港口信息,我们需要将其转换为数值型数据。
总结一下,我们需要做以下数据的预处理,包括:
- 提取
Survived列的数据作为类别标签。 - 丢弃不需要的特征数据。
- 对数据进行转换,以便模型处理。例如性别数据,我们需要转换为0和1。
- 处理缺失的数据,这里用最简单的0值填充,在进阶教程中,我会用更高级的用法来进行处理。
""" 数据预处理 """ # 指定第一列作为行索引 train_data = pd.read_csv("./data/train.csv", index_col=0) # 丢弃无用的数据 train_data.drop(["Name", "Ticket", "Cabin"], axis=1, inplace=True) # print(train_data.head()) # 处理性别数据 train_data["Sex"] = (train_data["Sex"] == "male").astype(int) # male: 1 female: 0 # 处理港口数据 labels = train_data["Embarked"].unique().tolist() # 处理缺失数据:这里用最简单的0值填充 train_data = train_data.fillna(0)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
处理完的数据样本如下图所示:
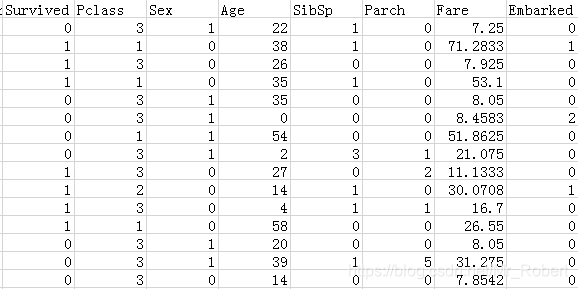
然后,我们需要将Survived列提取出来作为标签,并在原始数据集中将其丢弃,同时将数据集分成训练集和交叉验证集:
"""
拆分数据集
"""
from sklearn.model_selection import train_test_split
y = train_data["Survived"].values
X = train_data.drop("Survived", axis=1).values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
print("X_train shape:", X_train.shape, "X_test shape:", X_test.shape)
Out:
X_train shape: (712, 7) X_test shape: (179, 7)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
接下来,我们利用决策树模型对数据进行拟合,并计算得分:
"""
模型训练
"""
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
test_score = clf.score(X_test, y_test)
print("train score:{0:.3f}; test score:{1:.3f}".format(train_score, test_score))
Out:
train score:0.979; test score:0.754
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
从输出结果来看,训练样本的评分很高,但交叉验证集的评分比较低。很明显,这是过拟合的现象。解决决策树过拟合的方法是剪枝,包括前剪枝和后剪枝。不幸的是,scikit-learn不支持后剪枝,但提供了一系列模型参数进行前剪枝。例如,我们通过max_depth参数限定决策树的深度,当决策树达到限定的深度时,就不再进行分裂了,这样在一定程度上可以避免过拟合。
""" 模型参数调优 """ import numpy as np # 优化模型参数:max_depth def cv_score(d): """ 在不同depth值下,train_score和test_score的值 :param d: max_depth值 :return: (train_score, test_score) """ clf = DecisionTreeClassifier(max_depth=d) clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) return (train_score, test_score) # 指定参数的范围,训练模型计算得分 depths = range(2, 15) scores = [cv_score(d) for d in depths] train_scores = [s[0] for s in scores] cv_scores = [s[1] for s in scores] # 找出交叉验证集评分最高的模型参数 best_score_index = np.argmax(cv_scores) best_score = cv_scores[best_score_index] best_param = depths[best_score_index] # 找出对应的参数 print("best param: {0}; best score: {1:.3f}".format(best_param, best_score)) Out: best param: 4; best score: 0.844
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
可以看到,针对模型深度这个参数,最优值为4, 其对应的交叉验证集的评分为0.844,具有较大的提升。我们可以把模型参数和模型评分可视化,更加直观的观察变化规律:
"""
参数调优可视化
"""
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 4), dpi=200)
plt.grid()
plt.xlabel("Max depth of Decision Tree")
plt.ylabel("score")
plt.plot(depths, cv_scores, ".g--", label="cross validation score")
plt.plot(depths, train_scores, ".r--", label="training score")
plt.legend()
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
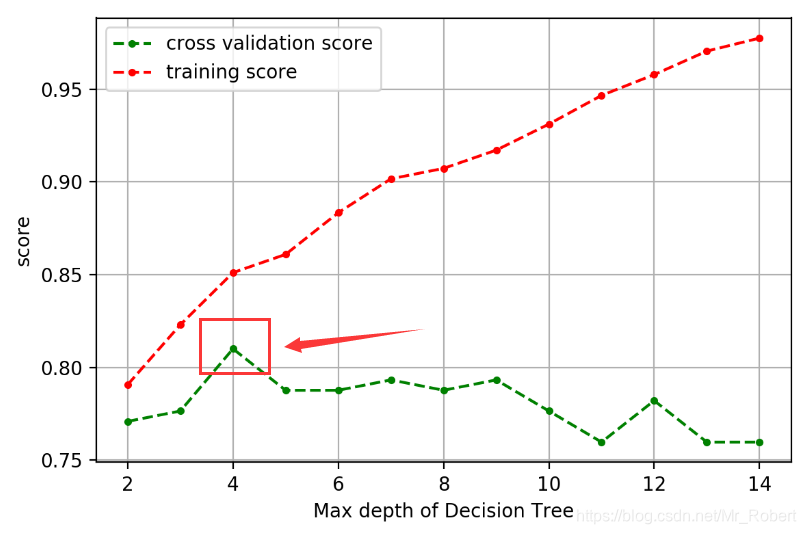
我们可以使用同样的方法,考察参数mini_impurity_split。这个参数用来指定信息熵或者基尼不纯度的阈值,当决策树分裂后,其信息增益低于这个阈值时,则不再分裂:
# 优化模型参数:在criterion="gini"下的min_impurity_split def cv_score(val): """ 在不同depth值下,train_score和test_score的值 :param d: max_depth值 :return: (train_score, test_score) """ clf = DecisionTreeClassifier(criterion="gini", min_impurity_split=val) clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) return (train_score, test_score) # 指定参数的范围,训练模型计算得分 values = np.linspace(0, 0.5, 50) scores = [cv_score(v) for v in values] train_scores = [s[0] for s in scores] cv_scores = [s[1] for s in scores] # 找出交叉验证集评分最高的模型参数 best_score_index = np.argmax(cv_scores) best_score = cv_scores[best_score_index] best_param = values[best_score_index] # 找出对应的参数 print("best param: {0}; best score: {1:.3f}".format(best_param, best_score)) # 画出模型参数与模型评分的关系 plt.figure(figsize=(6, 4), dpi=200) plt.grid() plt.xlabel("Min_impurity_split of Decision Tree") plt.ylabel("score") plt.plot(values, cv_scores, ".g--", label="cross validation score") plt.plot(values, train_scores, ".r--", label="training score") plt.legend() plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
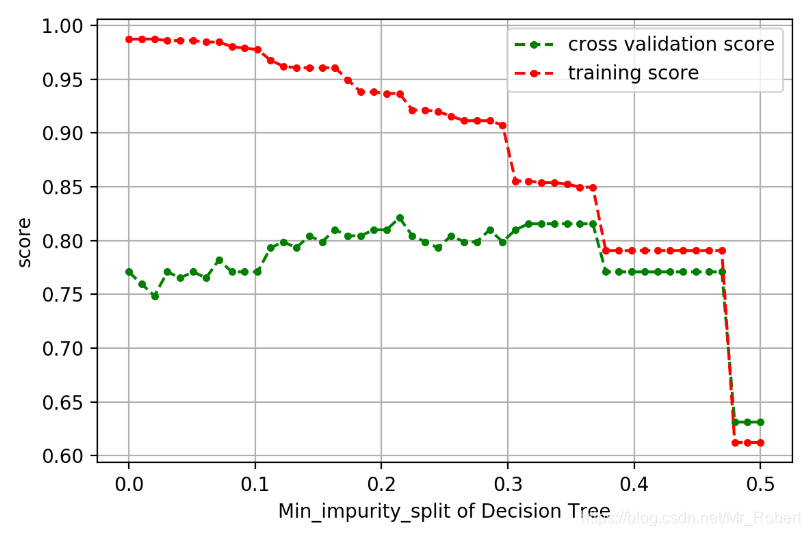
看到这你可能想到上述的模型参数优化方法有两个问题:
- 数据不稳定
- 不能一次选择多个参数
问题一的原因在于数据集划分是随机的,导致每次训练集是有差异的,训练出来的模型也有差异。解决这个问题的方法是多次计算求平均值。具体来讲,就是针对模型的某个特定参数值,多次划分数据集,多次训练模型,计算出这个参数值的最低评分、最高评分及平均评分。之前使用过这个方法—K折交叉验证。【机器学习算法笔记系列】K-近邻(KNN)算法详解和实战
关于问题二,sklearn.model_selection包中提供了大量模型选择和评估的工具供我们使用。针对以上问题,可以使用GridSearchCV类来解决,我们先简单介绍下GridSearchCV:
"""
模型参数选择工具包
"""
from sklearn.model_selection import GridSearchCV
thresholds = np.linspace(0, 0.5, 50)
# 设置参数矩阵
param_grid = {"min_impurity_split": thresholds}
clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5)
clf.fix(X, y)
print("best param: {0} \nbest score: {1}".format(clf.best_params_, clf.best_score_))
Out:
best param: {'min_impurity_split': 0.2040816326530612}
best score: 0.8215488215488216
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
其中关键的参数是param_grid,它是一个字典,字典关键字所对应的值是一个列表。GridSearchCV会枚举列表里的所有值来构建模型,多次计算训练模型,并计算模型评分,最终得到指定参数值的平均评分及标准差。另外一个关键的参数是cv,它用来指定交叉验证集的生成规则,代码中cv=5表示每次计算都把数据集分成5份,其中一份作为交叉验证集,其他作为训练集。最终得到的最优参数及最优评分保存在clf.best_params_和clf.best_score_里。此外,clf.cv_results_保存了计算过程的中间结果。
接下来看一下如何在多组参数之间选择最优的参数:
from sklearn.model_selection import GridSearchCV entropy_thresholds = np.linspace(0, 1, 50) gini_thresholds = np.linspace(0, 0.5, 50) # 设置参数矩阵 param_grid = [{"criterion": ["entropy"], "min_impurity_split": entropy_thresholds}, {"criterion": ["gini"], "min_impurity_split": gini_thresholds}, {"max_depth": range(2, 10)}, {"min_samples_split": range(2, 30, 2)}] clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5) clf.fit(X, y) print("best param: {0} \nbest score: {1}".format(clf.best_params_, clf.best_score_)) Out: best param: {'criterion': 'entropy', 'min_impurity_split': 0.5306122448979591} best score: 0.8282828282828283
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
最后,使用最优参数的决策树到底是什么样呢?我们可以使用sklearn.tree.export_graphviz()函数把决策树模型参数导出到文件中,然后使用graphviz工具包生成决策树示意图:
""" 生成决策树图形 """ """ 生成决策树图形 """ from sklearn.tree import export_graphviz clf = DecisionTreeClassifier(criterion='entropy', min_impurity_split=0.5306122448979591) clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) print('train score: {0:.3f}; test score: {1:.3f}'.format(train_score, test_score)) # 导出 titanic.dot 文件 with open("titanic.dot", 'w') as f: f = export_graphviz(clf, out_file=f) Out: train score: 0.930; test score: 0.832
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
生成决策树图形:
- 在电脑上安装 graphviz
- 运行
dot -Tpng titanic.dot -o titanic.png - 在当前目录查看生成的决策树 titanic.png
决策树实战泰坦尼克幸存者预测全部代码:
__author__ = "fpZRobert" """ 决策树算法—泰坦尼克幸存者预测 """ import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.model_selection import GridSearchCV from sklearn.tree import DecisionTreeClassifier,export_graphviz import warnings warnings.filterwarnings('ignore') """ 加载数据 """ # 加载训练集 train_data = pd.read_csv('./data/train.csv') test_data = pd.read_csv('./data/test.csv') # 查看数据形状 print("train_data.shape: ", train_data.shape) # (981, 12) print(train_data.head()) # 查看数据前5行 # 数据信息总览 print(train_data.info()) """ 数据预处理 """ # 指定第一列作为行索引 train_data = pd.read_csv("./data/train.csv", index_col=0) # 丢弃无用的数据 train_data.drop(["Name", "Ticket", "Cabin"], axis=1, inplace=True) # print(train_data.head()) # 处理性别数据 train_data["Sex"] = (train_data["Sex"] == "male").astype(int) # male: 1 female: 0 # 处理港口数据 labels = train_data["Embarked"].unique().tolist() train_data["Embarked"] = train_data["Embarked"].apply(lambda n: labels.index(n)) # 处理缺失数据:这里用最简单的0值填充 train_data = train_data.fillna(0) """ 拆分数据集 """ y = train_data["Survived"].values X = train_data.drop("Survived", axis=1).values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) print("X_train shape:", X_train.shape, "X_test shape:", X_test.shape) """ 模型训练 """ clf = DecisionTreeClassifier() clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) print("train score:{0:.3f}; test score:{1:.3f}".format(train_score, test_score)) """ 模型参数调优 """ # 优化模型参数:max_depth def cv_score(d): """ 在不同depth值下,train_score和test_score的值 :param d: max_depth值 :return: (train_score, test_score) """ clf = DecisionTreeClassifier(max_depth=d) clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) return (train_score, test_score) # 指定参数的范围,训练模型计算得分 depths = range(2, 15) scores = [cv_score(d) for d in depths] train_scores = [s[0] for s in scores] cv_scores = [s[1] for s in scores] # 找出交叉验证集评分最高的模型参数 best_score_index = np.argmax(cv_scores) best_score = cv_scores[best_score_index] best_param = depths[best_score_index] # 找出对应的参数 print("best param: {0}; best score: {1:.3f}".format(best_param, best_score)) """ 参数调优可视化 """ plt.figure(figsize=(6, 4), dpi=200) plt.grid() plt.xlabel("Max depth of Decision Tree") plt.ylabel("score") plt.plot(depths, cv_scores, ".g--", label="cross validation score") plt.plot(depths, train_scores, ".r--", label="training score") plt.legend() plt.show() # 优化模型参数:在criterion="gini"下的min_impurity_split def cv_score(val): """ 在不同depth值下,train_score和test_score的值 :param d: max_depth值 :return: (train_score, test_score) """ clf = DecisionTreeClassifier(criterion="gini", min_impurity_split=val) clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) return (train_score, test_score) # 指定参数的范围,训练模型计算得分 values = np.linspace(0, 0.5, 50) scores = [cv_score(v) for v in values] train_scores = [s[0] for s in scores] cv_scores = [s[1] for s in scores] # 找出交叉验证集评分最高的模型参数 best_score_index = np.argmax(cv_scores) best_score = cv_scores[best_score_index] best_param = values[best_score_index] # 找出对应的参数 print("best param: {0}; best score: {1:.3f}".format(best_param, best_score)) # 画出模型参数与模型评分的关系 plt.figure(figsize=(6, 4), dpi=200) plt.grid() plt.xlabel("Min_impurity_split of Decision Tree") plt.ylabel("score") plt.plot(values, cv_scores, ".g--", label="cross validation score") plt.plot(values, train_scores, ".r--", label="training score") plt.legend() plt.show() # """ # 模型参数选择工具包 # """ # thresholds = np.linspace(0, 0.5, 50) # # 设置参数矩阵 # param_grid = {"min_impurity_split": thresholds} # clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5) # clf.fit(X, y) # print("best param: {0} \nbest score: {1}".format(clf.best_params_, clf.best_score_)) # 参数 entropy_thresholds = np.linspace(0, 1, 50) gini_thresholds = np.linspace(0, 0.5, 50) # 设置参数矩阵 param_grid = [{"criterion": ["entropy"], "min_impurity_split": entropy_thresholds}, {"criterion": ["gini"], "min_impurity_split": gini_thresholds}, {"max_depth": range(2, 10)}, {"min_samples_split": range(2, 30, 2)}] clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5) clf.fit(X, y) print("best param: {0} \nbest score: {1}".format(clf.best_params_, clf.best_score_)) """ 生成决策树图形 """ clf = DecisionTreeClassifier(criterion='entropy', min_impurity_split=0.5306122448979591) clf.fit(X_train, y_train) train_score = clf.score(X_train, y_train) test_score = clf.score(X_test, y_test) print('train score: {0:.3f}; test score: {1:.3f}'.format(train_score, test_score)) # 导出 titanic.dot 文件 with open("titanic.dot", 'w') as f: f = export_graphviz(clf, out_file=f)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179



