聚类算法用于降维，KMeans的矢量量化应用_聚类分析可以把高维数据降维吗

---

前言

在本案例中添加了不适用KMeans来进行矢量量化，随机抽取64个当作质心，与使用KMeans矢量量化做出了对比

---

案例：聚类算法用于降维，KMeans的矢量量化应用

K-Means聚类最重要的应用之一是非结构数据（图像，声音）上的矢量量化（VQ）。非结构化数据往往占用比较多的储存空间，文件本身也会比较大，运算非常缓慢，我们希望能够在保证数据质量的前提下，尽量地缩小非结构化数据的大小，或者简化非结构化数据的结构。矢量量化就可以帮助我们实现这个目的。KMeans聚类的矢量量化本质是一种降维运用，但它与我们之前学过的任何一种降维算法的思路都不相同。特征选择的降维是直接选取对模型贡献最大的特征，PCA的降维是聚合信息 ，而矢量量化的降维是在同等样本量上压缩信息的大小，即不改变特征的数目也不改变样本的数目，只改变在这些特征下的样本上的信息量。

对于图像来说，一张图片上的信息可以被聚类如下表示：

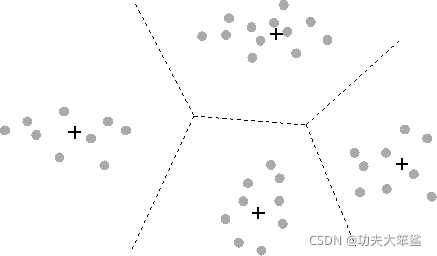
这是一组40个样本的数据，分别含有40组不同的信息(x1,x2)。我们将代表所有样本点聚成4类，找出四个质心，我们认为，这些点和他们所属的质心非常相似，因此他们所承载的信息就约等于他们所在的簇的质心所承载的信息。于是，我们可以使用每个样本所在的簇的质心来覆盖原有的样本，有点类似四舍五入的感觉，类似于用1来代替0.9和0.8。

这样，40个样本带有的40种取值，就被我们压缩了4组取值，虽然样本量还是40个，但是这40个样本所带的取值其实只有4个，就是分出来的四个簇的质心。

**用K-Means聚类中获得的质心来替代原有的数据，可以把数据上的信息量压缩到非常小，但又不损失太多信息。**我们接下来就通过一张图图片的矢量量化来看一看K-Means如何实现压缩数据大小，却不损失太多信息量。

1. 导入需要的库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

#对两个序列中的点进行距离匹配的函数
#函数pairwise_distances_argmin(x1,x2,axis) #x1和x2分别是序列
#用来计算x2中的每个样本到x1中的每个样本点的距离，并返回和x2相同形状的，x1中对应的最近的样本点的索引
from sklearn.metrics import pairwise_distances_argmin 

from sklearn.datasets import load_sample_image #导入图片数据所用的类
from sklearn.utils import shuffle #用来打乱有序序列，可以对数组，列表，DataFrame等都可以进行打乱
1
2
3
4
5
6
7
8
9
10
11

2.导入数据，探索数据（里面的内容是探索图像数据的一个固定的流程）

这些是探索图像数据的一个固定的流程，看数据的类型，三个维度的数据是什么样的，有多少种不同种类的颜色，图片是什么样的

# 实例化，导入颐和园的图片
china = load_sample_image("china.jpg")
china
#可以看到是一个三维的数组
1
2
3
4

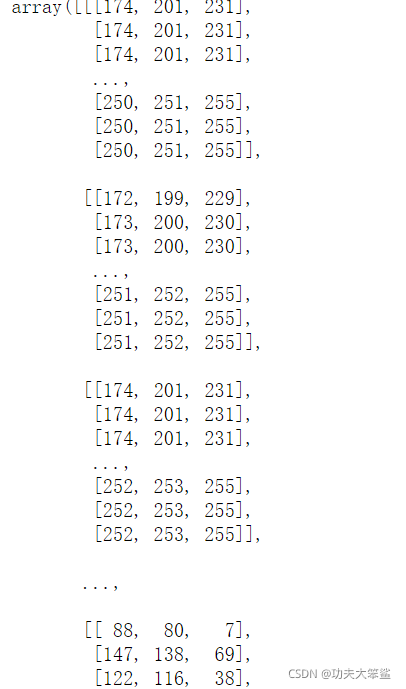
#查看图片的数据类型
china.dtype
#uint8是典型的图片类型
1
2
3

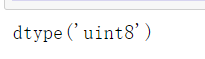
china.shape
#长度 x 宽度 x 特征 > 三个数决定的颜色
#表示长为427，宽为640，也就是一共有427*640个像素点，每个像素点有3个特征
1
2
3

#三个数决定一个颜色
china[0][0]
1
2

#看这些数据一共是多少种不同的颜色，使用drop_duplicates()来进行删除重复值
#首先将长宽进行合并
newimag = china.reshape((427*640),3)

newimag.shape
1
2
3
4
5

import pandas as pd

#drop_duplicates删除表中重复的值
pd.DataFrame(newimag).drop_duplicates().shape
#现在就剩9w多种不同的颜色了
1
2
3
4
5

#图像可视化
plt.figure(figsize=[15,15])

#imshow必须导入一个三维数组
plt.imshow(china)
1
2
3
4
5

#拓展
#查看模块中的另一张图片
flower = load_sample_image("flower.jpg")
plt.figure(figsize=(15,15))
plt.imshow(flower)
1
2
3
4
5

图像探索完毕，我们了解了，图像现在有9W多种颜色。我们希望来试试看，能否使用K-Means将颜色压缩到64种，还不严重损耗图像的质量。为此，我们要使用K-Means来将9W种颜色聚类成64类，然后使用64个簇的质心来替代全部的9W种颜色，记得质心有着这样的性质：簇中的点都是离质心最近的样本点。

**为了比较，我们还要画出随机压缩到64种颜色的矢量量化图像。**我们需要随机选取64个样本点作为随机质心，计算原数据中每个样本到它们的距离来找出离每个样本最近的随机质心，然后用每个样本所对应的随机质心来替换原本的样本。两种状况下，我们观察图像可视化之后的状况，以查看图片信息的损失。

在这之前，我们需要把数据处理成sklearn中的K-Means类能够接受的数据。

---

3. 决定超参数，数据预处理

#KMeans只能带入2维的数据
#首先先对china进行归一化处理，plt.imshow在浮点数上表现非常优异，在这里我们把china中的数据，转换为浮点数，压缩到[0,1]之间
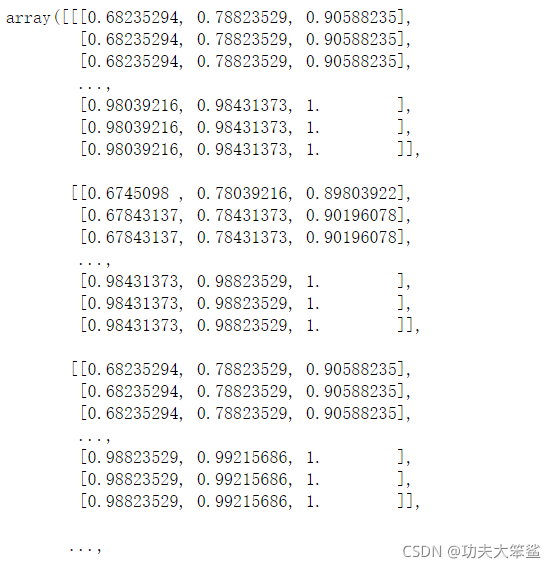
china = np.array(china, dtype=np.float64) / china.max()
china
1
2
3
4

#看有没有小于0
(china<0).sum()
>0

#看有没有大于一的
(china>1).sum()
>0
1
2
3
4
5
6
7

#把china从图像格式，转换成矩阵格式
w, h, d = original_shape = tuple(china.shape)

#将这个图像的长，宽，维度都取出来进行一个储存
1
2
3
4

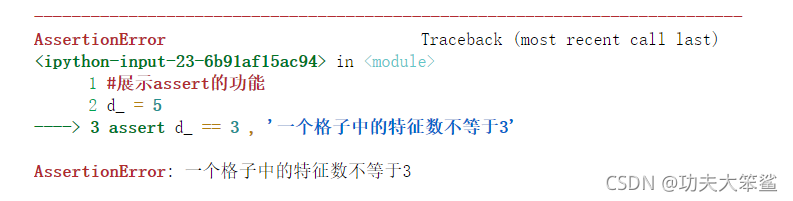
在这里引入assert，**assert就是如果不满足assert后面的条件，就会输出自己定义的报错，**下面展示一下assert的功能

#展示assert的功能
d_ = 5
assert d_ == 3 , '一个格子中的特征数不等于3'
1
2
3

#这样就不会报错
assert d_ == 5 , '一个格子中的特征数不等于3'
1
2

回归正题

#非常重要的一点就是，特征数一定不可以改变，不论什么改变特征数d都不能发生改变
#使用assert d==3，代表如果d不等于3，就会报错
assert d == 3 , '特征应该为3'
1
2
3

#np.reshape(a, newshape, order='C'), reshape函数的第一个参数a是要改变结构的对象，第二个参数是要改变的新结构
#展示np.reshape的效果

#改变china的结构，KMeans只能使用二维的
image_array = np.reshape(china,(w * h, d)) #reshape改变结构
image_array
1
2
3
4
5
6

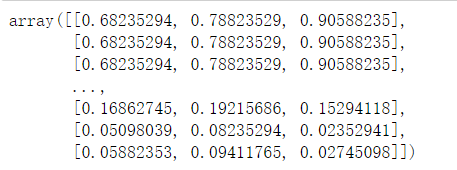
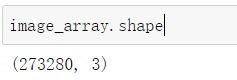
对比一下reshape和np.reshape， 其实两种的结果是一样的，看喜欢用哪种就可以用哪种

a = np.random.random((2,4))
a
1
2

a.reshape(4,2)
1

a.reshape(4,2).shape
1

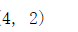
a.shape
1

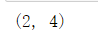
np.reshape(a,(4,2))
1

4. 对数据进行K-Means的矢量量化

首先看一下shuffle的作用，就是对数组进行打乱，假如是a[x][y],他只打乱[x]，对[y]的不会进行打乱

shuffle(image_array, random_state=0)
1

#可以看到我们要使用的数据是273280行
#我们假设n_clusters=64,分64簇
#在KMeans聚类算法一文中的2.1.1.4说到，如果数据量大，可以使用predict，使用部分数据来寻找质心
#在这里我们使用1000个数据来寻找质心
n_clusters = 64

#使用shuffle来对数据进行打乱顺序，成为随机分布的形式，然后选取前1000个作为训练的样本
image_array_sample = shuffle(image_array, random_state=0)[:1000]

#进行实例化
kmeans = KMeans(n_clusters = n_clusters, random_state=0).fit(image_array_sample)

#查看选取到的64个质心
kmeans.cluster_centers_
1
2
3
4
5
6
7
8
9
10
11
12
13
14

#找出质心后，按照已存在的质心来对所有的数据进行聚类
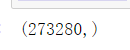
labels = kmeans.predict(image_array)
labels.shape
1
2
3

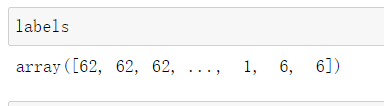
#通过集合的去重性质，可以看到分为了64簇
set(labels)
1
2

#为了不破坏原数据，所以对image_array进行copy
image_kmeans = image_array.copy()

image_kmeans #27W个样本点，9W多种不同的颜色（像素点）
1
2
3
4

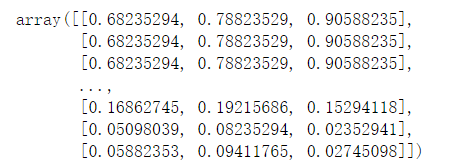
labels #这27W个样本点所对应的簇的质心的索引
1

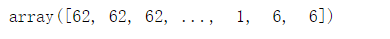
#labels[0]是簇的编号，这段代码的意思是看这个编号的簇的质心是什么
kmeans.cluster_centers_[labels[0]]
1
2

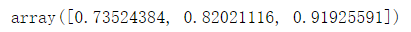
#使用质心来替换所有的样本
#通过循环来对每一个样本进行替换成相应簇的质心
#他们所承载的信息就约等于他们所在的簇的质心所承载的信息。于是，我们可以使用每个样本所在的簇的质心来覆盖原有的样本
for i in range(w*h):
    image_kmeans[i] = kmeans.cluster_centers_[labels[i]]

#查看生成的新图片信息
image_kmeans
1
2
3
4
5
6
7
8

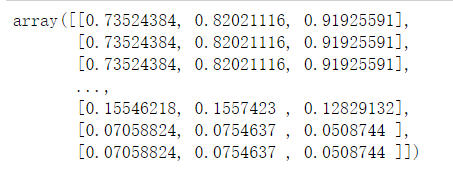
image_kmeans.shape
1

#在上面得到，使用质心替换之前的颜色种类有9w多种，在使用质心替换之后颜色种类就剩64种了
pd.DataFrame(image_kmeans).drop_duplicates().shape
1
2

#接下来就是要看我们通过KMeans处理之后的图像是什么样的
#imshow只能输入三维的数据，所以在这里我们要对image_kmeans恢复成图片原来的结构
image_kmeans = image_kmeans.reshape(w,h,d)
image_kmeans.shape
1
2
3
4

5. 对数据进行随机的矢量量化

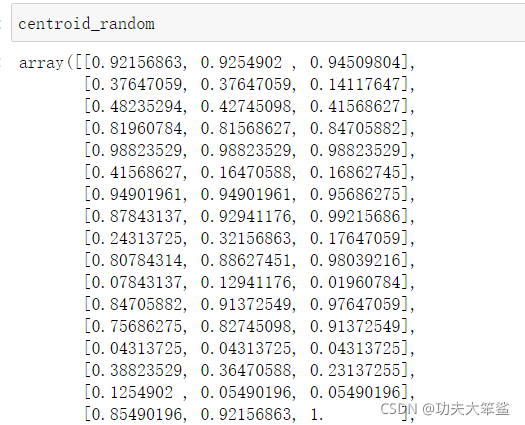
#n_clusters在上面定义的是64，这里就是直接先对原数据image_array进行打乱，然后取出前64个直接作为质心
centroid_random = shuffle(image_array, random_state=0)[:n_clusters]
centroid_random.shape
1
2
3

#函数pairwise_distances_argmin(x1,x2,axis) #x1和x2分别是序列
#用来计算x2中的每个样本到x1中的每个样本点的距离，并返回和x2相同形状的，x1中对应的最近的样本点的索引
#在这里就是计算image_array与随机选出来的64个质心进行计算，并且选取最小的那个簇的编号进行返回，这样就完成了分簇
labels_random = pairwise_distances_argmin(centroid_random,image_array,axis=0)
1
2
3
4

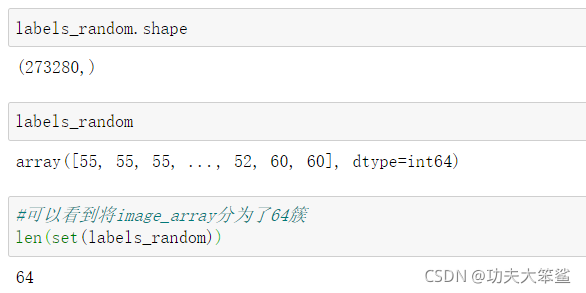
#使用随机质心来替换所有样本，同上面的思想相同
image_random = image_array.copy()

for i in range(w*h):
    image_random[i] = centroid_random[labels_random[i]]

#恢复图片的结构，同上面的思想相同
image_random = image_random.reshape(w,h,d)
image_random.shape
1
2
3
4
5
6
7
8
9

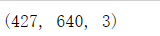
6. 将原图，按KMeans矢量量化和随机矢量量化的图像绘制出来

#原数据
plt.figure(figsize=(10,10))
plt.axis('off')
plt.title('Original image (96,615 colors)')
plt.imshow(china)

#使用kmeans矢量量化之后的图像
plt.figure(figsize=(10,10))
plt.axis('off')
plt.title('Quantized image (64 colors, K-Means)')
plt.imshow(image_kmeans)

#随机选取64个为质心的图像
plt.figure(figsize=(10,10))
plt.axis('off')
plt.title('Quantized image (64 colors, Random)')
plt.imshow(image_random)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

总结

可以看到通过KMeans矢量量化之后的图片，颜色并没有改变很多，在塔的上面颜色依旧鲜艳，只不过在湖面和天空，信息稍微有一些损失。

没有使用KMeans矢量量化，使用随机选取质心的方法来进行矢量量化，得到的图片明显暗淡了许多，信息损失的比较多

对比两种方法，可以看出KMeans还是非常强大的，都是64种的分簇，kmeans表现要比随机的要好