非常简单！用Java实现一个简单的向量数据库雏形。_java向量数据库

概述

向量数据库是用来解决高维向量数据管理和查询的问题。它能够有效地存储、索引和查询大规模高维度向量数据，并提供高性能和高效的相似度搜索。传统的关系型数据库或文档数据库在处理高维向量数据时可能会遇到诸多问题。比如在高维空间中，数据点之间的距离计算变得复杂和耗时，同时导致存储和查询的成本增加。常用的欧氏距离等度量方式可能失效，需要使用更复杂的相似度度量方法，如余弦相似度、汉明距离等。传统数据库不擅长存储和索引高维向量数据，导致占用更多的存储空间和查询时间。
因此为了解决这些问题，诞生了向量数据库。向量数据库采用专门的数据结构和算法，可以高效地存储大规模高维向量数据。它将向量作为基本单位，而不是将其拆分成标量进行存储。它提供了针对高维向量的索引机制，如KD-Tree、球树、LSH等。这些索引结构可以加速相似度搜索，从而快速找到与查询向量相似的向量数据。令人兴奋的是，它还支持基于相似度的查询，可以根据给定的查询向量找到与其接近的向量数据。它使用特定的相似度度量方法，如余弦相似度或欧氏距离，进行准确和高效的搜索。与此同时它还可以采用各种传统压缩和编码技术，可以减少存储空间的消耗，提高空间利用率和数据访问效率，支持分布式部署和并行化处理，以提供更好的性能和可伸缩性。
向量数据库在许多领域中发挥着重要作用，如图像和视频检索、文本语义搜索、推荐系统、工业物联网和生物信息学等。它们广泛应用于各种场景，以提供快速的相似度搜索和高效的高维向量数据管理能力。

索引结构

最常见的向量数据库索引结构是KD-Tree。它是一种用于高效存储和检索k维向量数据的数据结构。它是一种二叉树，每个节点对应着一个k维向量，并且通过划分空间将向量依次放置在树的节点上。
KD-Tree根据不同维度上的分割平面将向量划分为两个子集。例如，在一个二维KD-Tree中，可以先基于X轴将数据划分为左右子集，然后基于Y轴将左右子集各自再划分为两个子集，依次类推。在每一层中，KD-Tree使用不同的维度进行分割。
除了KD-Tree，还有其他一些常用的索引结构可用于高效存储和检索向量数据：
Ball Tree：Ball Tree（球树）是一种二叉树结构，类似于KD-Tree。不同之处在于它使用球体来划分空间，而不是平面或超平面。球树可以更好地处理非均匀分布的数据集，适合处理包围球和半径搜索等查询。
R-Tree：R-Tree（区域树）是一种多维索引结构，用于组织空间对象。它能够高效地处理范围查询和近邻查询，并支持动态插入和删除操作。R-Tree将空间对象划分为不相交的矩形区域，通过选择合适的叶子节点进行进一步搜索。
Cover Tree：Cover Tree（覆盖树）是一种用于高维近邻搜索的数据结构。它通过将数据点放置在距离的指数级别上构建树结构。Cover Tree能够高效地找到最近邻居，并且在构建和查询过程中具有良好的时间和空间复杂度。
VP-Tree：VP-Tree（Vantage Point Tree）也是一种用于高维近邻搜索的索引结构。VP-Tree通过选择代表点作为分割点，根据代表点与其他数据点的距离构建树形结构。它能够高效处理范围搜索和近似最近邻查询，并且对于高维数据集具有较好的性能。
LSH（Locality Sensitive Hashing）：LSH是一种基于哈希的索引算法，用于高维近似近邻搜索。它使用哈希函数将相似的向量映射到同一个桶中，从而能够快速找到近似的近邻。LSH适用于大规模数据集和高维数据的查询，并具有较好的可扩展性。

以下是一些常见的索引结构的优缺点：

KD-Tree：

优点：支持高效的最近邻查询和范围搜索；适用于低维数据集；易于理解和实现。
缺点：对于高维数据集，可能会出现"维度灾难"的问题，性能下降；不支持动态插入和删除操作。
Ball Tree：

优点：适用于具有非均匀分布的数据集；能够更好地处理包围球和半径搜索等查询。
缺点：相较于其他索引结构，构建和查询速度较慢；需要更多的内存空间。
R-Tree：

优点：支持范围查询和近邻查询；适用于空间对象的组织和检索；支持动态插入和删除操作。
缺点：R-Tree在维度较高时，可能会遇到"维度灾难"的问题导致性能下降。
Cover Tree：

优点：在构建和查询过程中具有良好的时间和空间复杂度；能够高效获取最近邻居。
缺点：构建Cover Tree相对复杂；不适用于范围查询。
VP-Tree：

优点：适用于高维近邻搜索；能够高效处理范围搜索和近似最近邻查询。
缺点：构建VP-Tree相对复杂；与数据分布和距离度量相关。
LSH（Locality Sensitive Hashing）：

优点：适用于大规模数据集和高维数据的近似近邻查询；具有较好的可扩展性。
缺点：通过哈希函数进行近似匹配，可能会引入误差；查询结果的准确性相对较低。

什么是维度灾难？

维度灾难是指在高维空间中，由于数据点之间的距离变得稀疏和无效，导致查询性能下降的问题。为了解决维度灾难，可以考虑以下几种方法：
数据预处理和特征选择：通过对数据进行预处理和特征选择，可以去除冗余和不相关的特征，减少维度的同时保留有用的信息。这可以提高索引结构和查询算法的性能。
维度约减（Dimensionality Reduction）：维度约减技术可以将高维数据转化为低维表示，从而降低数据的维度并保留关键的特征和信息。常见的维度约减方法包括主成分分析（PCA）、线性判别分析（LDA）和t-SNE等。
局部敏感哈希（Locality Sensitive Hashing，LSH）：LSH是一种基于哈希的索引算法，能够将近似的近邻映射到相同的桶中。通过使用哈希函数将相似的向量聚集在一起，可以有效地减少维度对查询的影响，并提高查询的效率。
改进的索引结构：针对高维数据，可以使用特定设计的索引结构来解决维度灾难问题。例如，M-Tree、VA-File和Pivot-Based Partitioning等索引结构都是为高维数据而设计的，并采用不同的策略来划分和组织数据。
近似算法：近似算法通过牺牲一定程度的精确性来优化查询性能。例如，使用近似最近邻算法（Approximate Nearest Neighbor，ANN）可以在保证一定误差范围内找到近似的最近邻，从而加快查询速度。

KD-Tree的结构

                    Node
                 /         \
           left            right
          /     \        /      \
 Nodes...  Node  Node   Node    Node
1
2
3
4
5

KD 树是一种二叉树结构，每个节点都代表一个向量数据点。根节点位于树的顶部，每个节点可以有左子节点和右子节点。

每个节点的左子节点和右子节点分别代表根据划分轴划分得到的两个子空间中的向量数据点。根据构建 KD 树的算法，在每一层中，节点的划分轴会不断地在各个维度之间循环。左子树代表小于当前节点的数据点，而右子树代表大于当前节点的数据点。

每个节点包含以下信息：

point：向量数据点。
axis：划分轴的索引。
left：左子树。
right：右子树。

实际的 KD 树结构取决于数据集中的向量点以及划分轴的选择，因此实际的 KD 树可能会有不同的形状和层次结构。

如果我们将KD-Tree按三维展示，则是下面这个样子（这是个立方体，图画的不太好，勿喷）：

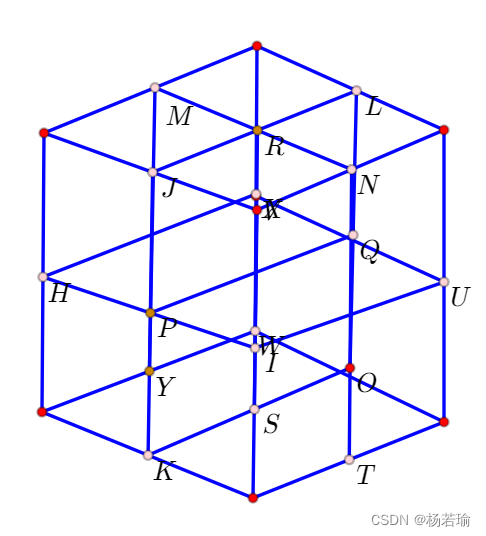
一个简单的KD-Tree例子

我们现在实现一个存储向量的KD-Tree：

import java.util.Comparator;

class Node {
    double[] point;  // 向量数据点
    int axis;        // 划分轴
    Node left;       // 左子树
    Node right;      // 右子树

    public Node(double[] point, int axis) {
        this.point = point;
        this.axis = axis;
        this.left = null;
        this.right = null;
    }
}

public class KDTree {
    private Node root;   // 根节点
    private int k;       // 数据点的维度

    public KDTree(int k) {
        this.root = null;
        this.k = k;
    }

    private Comparator<double[]> comparator = new Comparator<double[]>() {
        @Override
        public int compare(double[] p1, double[] p2) {
            return Double.compare(p1[k], p2[k]);
        }
    };

    public void build(double[][] points) {
        this.root = buildTree(points, 0);
    }

    private Node buildTree(double[][] points, int axis) {
        if (points == null || points.length == 0) {
            return null;
        }

        int median = points.length / 2;
        double[][] sortedPoints = sortPoints(points, median, axis);

        Node node = new Node(sortedPoints[median], axis);
        node.left = buildTree(Arrays.copyOfRange(sortedPoints, 0, median), (axis + 1) % this.k);
        node.right = buildTree(Arrays.copyOfRange(sortedPoints, median + 1, sortedPoints.length), (axis + 1) % this.k);

        return node;
    }

    private double[][] sortPoints(double[][] points, int median, int axis) {
        Arrays.sort(points, comparator);
        return points;
    }

    public double[] search(double[] target) {
        return searchNode(this.root, target);
    }

    private double[] searchNode(Node node, double[] target) {
        if (node == null) {
            return null;
        }

        if (Arrays.equals(node.point, target)) {
            return node.point;
        }

        if (target[node.axis] < node.point[node.axis]) {
            return searchNode(node.left, target);
        } else {
            return searchNode(node.right, target);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

首先我们定义了一个 ​Node​ 类，表示 KD 树中的节点。每个节点有以下属性：​point​ 表示向量数据点，​axis​ 表示划分轴的索引， ​left​ 和 ​right​ 分别表示左子树和右子树。

然后定义了 ​KDTree​ 类，表示 KD 树。每个 KD 树对象包含一个根节点 ​root​ 和数据点的维度 ​k​。

在 ​KDTree​ 类中，通过构造函数初始化 KD 树的维度 ​k​ 和根节点 ​root​。并且使用比较器 ​comparator​ 对数据点进行排序，以便在建树时进行划分。

​​build​ 方法用于构建 KD 树。它使用递归的方式，通过 ​buildTree​ 方法来构建树。​buildTree​ 方法接收一个 ​points​ 参数，表示要构建树的数据点集合。根据当前轴 ​axis​ 的值将数据点集合划分成左子树和右子树，并创建当前节点，然后递归构建左右子树。

​​sortPoints​ 方法使用比较器 ​comparator​ 对输入的点集进行排序，并返回排序后的结果。

​​search​ 方法用于搜索与目标点最相似的数据点。它调用 ​searchNode​ 方法，在树中递归搜索节点。​searchNode​ 方法首先检查当前节点是否为目标点，如果是则返回当前节点，否则根据目标点在当前轴的值与节点进行比较，决定继续在左子树或右子树中搜索。

然后我们去尝试使用一下：

public class KDTreeDemo {
    public static void main(String[] args) {
        double[][] points = {
            {2, 3},
            {4, 5},
            {6, 9}
        };

        double[] target = {4, 6};

        KDTree tree = new KDTree(2);
        tree.build(points);
        double[] result = tree.search(target);

        if (result != null) {
            System.out.println("找到");
        } else {
            System.out.println("未找到");
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

实际应用

在企业级领域中，KD-Tree可以应用于许多场景。以下是一个示例，展示了如何使用KD-Tree解决一个企业级问题：人员调度。

假设有一个企业，需要对员工进行排班调度，以满足不同项目和工作需求。每个员工具有不同的技能和可用时间段。为了高效地进行排班调度，可以使用KD-Tree来存储员工的技能和可用时间信息，并根据项目和时间要求快速找到最适合的员工。

import java.util.Arrays;

class Employee {
    private String name;
    private double[] skills;
    private double[] availableTime;

    public Employee(String name, double[] skills, double[] availableTime) {
        this.name = name;
        this.skills = skills;
        this.availableTime = availableTime;
    }

    // Getters and setters
}

public class EmployeeScheduler {
    private KDTree kdTree;

    public EmployeeScheduler() {
        this.kdTree = new KDTree(2); // 假设员工的技能维度为2
    }

    public void addEmployee(Employee employee) {
        double[] point = new double[2]; // 假设技能维度为2
        point[0] = employee.getSkills()[0]; // 技能维度1
        point[1] = employee.getSkills()[1]; // 技能维度2

        kdTree.insert(point);
    }

    public String findBestEmployee(double[] requiredSkills) {
        double[] result = kdTree.search(requiredSkills);

        // 根据目标点找到最适合的员工
        if (result != null) {
            // 根据得到的点反向查找对应的员工
            Employee bestEmployee = getEmployeeByPoint(result);
            return bestEmployee.getName();
        } else {
            return null;
        }
    }

    private Employee getEmployeeByPoint(double[] point) {
        // 遍历员工列表，找到与给定点匹配的员工
        // 根据实际情况，可以使用哈希表或其他数据结构来提高搜索效率
        // 这里简化处理直接遍历
        for (Employee employee : employeeList) {
            double[] employeePoint = new double[2];
            employeePoint[0] = employee.getSkills()[0]; // 技能维度1
            employeePoint[1] = employee.getSkills()[1]; // 技能维度2

            // 判断两个点是否相等或匹配，这里按需求实现
            if (Arrays.equals(point, employeePoint)) {
                return employee;
            }
        }
        return null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

我们使用 ​double[]​数组来表示员工的技能和可用时间。当添加员工时，我们将技能向量插入KD-Tree中。在寻找最适合的员工时，我们根据所需的技能向量进行搜索。

基于这样的原理我们可以设计更复杂的向量数据库，如如何处理员工可用时间、如何计算匹配度等。对于多维度的向量问题，我们还可以尝试改变数据的表示形式、修改比较策略、使用距离度量等。

模糊性结果和确切性结果

向量数据库的模糊性结果和确切性结果是两种不同的查询结果类型，它们在适用场景和查询需求上有所区别。

---

确切性结果（Exact Results）：当我们在向量数据库中进行一个查询时，如果返回的结果是与查询向量完全匹配的向量数据点，那么这就是一个确切性结果。也就是说，确切性结果提供了与查询向量完全一致的数据点。在确切性查询中，我们希望找到与查询向量精确匹配的数据点。

确切性结果的应用：

数据去重：通过将向量作为特征来表示数据，可以使用确切性查询来查找和删除重复的数据点。
数据验证：可以使用确切性结果来验证数据是否存在，并进行数据完整性检查。
精确匹配搜索：当我们需要准确地找到某个或某些特定的数据点时，确切性结果非常有用。

---

模糊性结果（Fuzzy Results）：在向量数据库中，模糊性结果指的是与查询向量相似度高于某个设定阈值的向量数据点。模糊性结果并不要求与查询向量完全匹配，而是返回与查询向量相似的数据点。

模糊性结果的应用：
相似性搜索：在推荐系统、图像和视频检索、语义搜索等领域中，我们通常希望找到与查询向量相似的数据点，而不仅仅是精确匹配。模糊性结果可以提供一组相似的数据点，帮助用户在大型向量数据集中快速找到相关的数据。
探索和发现：在数据探索和发现阶段，模糊性结果可以帮助我们发现与我们兴趣或特定需求较为相似的数据点，从而了解数据的更多特征或关联性。

---

因此我们在使用向量数据库的时候，可以用模糊性结果和确切性结果来得到不同的数据结果集。

总结

向量数据库是近年来随着大数据和人工智能的发展而兴起的新型数据库技术。过去的几年中，向量数据库在学术界和行业领域得到了广泛关注和研究。早期的向量数据库主要关注高维向量数据的存储和索引技术，如KD树、球树等。随着深度学习和嵌入式向量表示的兴起，向量数据库开始应用于图像和视频检索、文本语义搜索、推荐系统等领域。
现如今，向量数据库已经从研究阶段进入了实际应用阶段。许多公司和组织已经开始在生产环境中使用向量数据库，以处理大规模高维向量数据。向量数据库的性能和功能不断提升，支持更多的查询类型和复杂的分析任务。
未来向量数据库在未来有巨大的发展潜力。随着人工智能和大数据的快速发展，对处理高维向量数据的需求会越来越大。向量数据库将继续改进其存储、索引和查询技术，提供更高效、更精确的相似度搜索和数据管理能力。向量数据库还有可能与其他数据库类型进行混合使用，以支持更丰富的查询和分析需求。
向量数据库已经在图像和视频检索、文本语义搜索、推荐系统、工业物联网、生物信息学等领域取得了成功的应用。它们被广泛用于解决大规模高维向量数据的存储、索引和查询问题。向量数据库的应用有助于提升信息检索和数据分析的效率和准确性。

对向量数据库的学习和掌握对于数据工程师、机器学习工程师和研究人员来说是非常有价值的。学习向量数据库可以深入了解高维向量数据的存储、索引和查询技术，可以为实际应用提供更有效的解决方案。