devbox
代码探险家
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

7 Go密码学（四） 非对称加密之RSA

作者：代码探险家 | 2024-07-19 23:11:41

赞

踩

encryptedbytes, err := rsa.encryptpkcs1v15(rand.reader, publickey, []byte(da

一、非对称加密概述

对称加密有非常好的安全性，其加解密计算的性能也较高，但其有两个重要缺点：

  • 加密的安全性依赖于秘钥的长度及复杂度；
  • 秘钥分发问题。

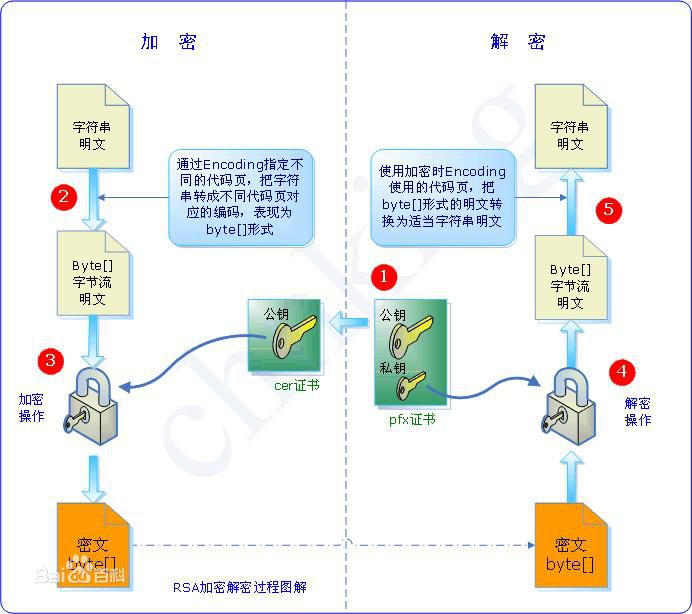
在如今开放的信息社会，秘钥的管理愈加困难，非公开的秘钥机制虽然破解较难，但还是有遭到攻击的可能性，由于对称加密需要加解密双方共同握有私钥，所有生成秘钥的一方必须分发给另一方才能进行安全通行，这就难免秘钥在网络中传输，网络是不可靠的，其有可能被拦截或篡改。于是就产生了公开秘钥体制，即服务方根据特定算法产生一对钥匙串，自己持有私钥小心保存，而公钥公开分发，在通信中，由公钥加密进行网络传输，而传输的信息只能由私钥解密，这就解决了秘钥分发的问。公开秘钥体制就是非对称加密，非对称加密一般有两种用途：

  • 安全信息传输：客户方持有公钥，通过公钥加密后发送给服务方，服务方通过私钥解密看到信息。
  • 数字签名：服务方持有公钥，客户方持有私钥，由服务方使用公钥进行数字签名，发送到客户方只能由私钥解密，这就保证了信息发送方来源安全的问题。

如今的非对称加密比较可靠的有RSA算法和ECC算法(椭圆曲线算法)，RSA的受众最多，但近年来随着比特币、区块链的兴起，ECC加密算法也越来越受到青睐。下面我们先介绍一下RSA加密算法的使用，ECC我们下一讲展开。

二、RSA加解密算法概述

RSA公开密钥密码体制。所谓的公开密钥密码体制就是使用不同的加密密钥与解密密钥，是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。在公开密钥密码体制中，加密密钥(即公开密钥)PK是公开信息，而解密密钥(即秘密密钥)SK是需要保密的。加密算法E和解密算法D也都是公开的。虽然解密密钥SK是由公开密钥PK决定的，由于无法计算出大数n的欧拉函数phi(N)，所以不能根据PK计算出SK。
正是基于这种理论，1978年出现了著名的RSA算法，它通常是先生成一对RSA 密钥，其中之一是保密密钥，由用户保存；另一个为公开密钥，可对外公开，甚至可在网络服务器中注册。为提高保密强度，RSA密钥至少为500位长，一般推荐使用1024位。这就使加密的计算量很大。为减少计算量，在传送信息时，常采用传统加密方法与公开密钥加密方法相结合的方式，即信息采用改进的DES或IDEA密钥加密，然后使用RSA密钥加密对话密钥和信息摘要。对方收到信息后，用不同的密钥解密并可核对信息摘要。
RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。RSA是被研究得最广泛的公钥算法，从提出到现今的三十多年里，经历了各种攻击的考验，逐渐为人们接受，截止2017年被普遍认为是最优秀的公钥方案之一。

RSA加解密图解

公钥密码体系都是要基于一个困难问题来保证其安全性的，RSA是基于大数分解，将一个即使是计算机也无能为力的数学问题作为安全壁垒是现代密码学的实现原理。讲述这类数学问题需要庞杂的数论基础，此相关部分在此不再展开，感兴趣的请出门右拐搜索欧几里得证明、欧拉函数等数论部分知识。

三、Go中使用RSA加解密

Go标准库中crypto/rsa包实现了RSA加解密算法，并通过crypto/x509包实现私钥序列化为ASN.1的DER编码字符串的方法，我们还使用编解码包encoding/pem(实现了PEM数据编码，该格式源自保密增强邮件协议，目前PEM编码主要用于TLS密钥和证书。)将公私钥数据编码为pem格式的证书文件。

X.509是一种非常通用的证书格式。所有的证书都符合ITU-T X.509国际标准，因此(理论上)为一种应用创建的证书可以用于任何其他符合X.509标准的应用。

PEM是存储证书和密钥的文件格式。PEM实质上是Base64编码的二进制内容

1.生成RSA公私钥文件
  1. import (
  2.     "crypto/rand"
  3.     "crypto/rsa"
  4.     "crypto/x509"
  5.     "encoding/pem"
  6.     "os"
  7. )
  8.  
  9. const (
  10.     PRIVATEFILE = "src/cryptography/myRSA/privateKey.pem"
  11.     PUBLICFILE  = "src/cryptography/myRSA/publicKey.pem"
  12. )
  13.  
  14. //生成公钥和私钥文件
  15.  
  16. func GenerateKey(bits int) error {
  17.     //生成私钥
  18.     //使用rsa中的GenerateKey方法生成私钥
  19.     privateKey, err := rsa.GenerateKey(rand.Reader, bits)
  20.     if err != nil {
  21.         return err
  22.     }
  23.  
  24.     //通过x509标准将得到的ras私钥序列化为ASN.1的DER编码字符串
  25.     PKCS1PrivateBytes := x509.MarshalPKCS1PrivateKey(privateKey)
  26.  
  27.     //将私钥字符串设置到pem格式块中
  28.     privateBlock := pem.Block{
  29.         Type:  "RSA Private Key",
  30.         Bytes: PKCS1PrivateBytes,
  31.     }
  32.  
  33.     //通过pem将设置好的数据进行编码，并写入磁盘文件
  34.     privateFile, err := os.Create(PRIVATEFILE)
  35.     if err != nil {
  36.         return err
  37.     }
  38.     defer privateFile.Close()
  39.     err = pem.Encode(privateFile, &privateBlock)
  40.     if err != nil {
  41.         return err
  42.     }
  43.  
  44.     //生成公钥
  45.     //从得到的私钥对象中将公钥信息取出
  46.     publicKey := privateKey.PublicKey
  47.  
  48.     //通过x509标准将得到的ras公钥序列化为ASN.1的DER编码字符串
  49.     PKCS1PublicBytes, err := x509.MarshalPKIXPublicKey(&publicKey)
  50.     if err != nil {
  51.         return err
  52.     }
  53.  
  54.     //将公钥字符串设置到pem格式块中
  55.     publicBlock := pem.Block{
  56.         Type:  "RSA Public Key",
  57.         Bytes: PKCS1PublicBytes,
  58.     }
  59.  
  60.     //通过pem将设置好的数据进行编码，并写入磁盘文件
  61.     publicFile, err := os.Create(PUBLICFILE)
  62.     if err != nil {
  63.         return err
  64.     }
  65.     defer publicFile.Close()
  66.     err = pem.Encode(publicFile, &publicBlock)
  67.     if err != nil {
  68.         return err
  69.     }
  70.  
  71.     return nil
  72. }
2.实现公钥加密，私钥解密的加密通信机制
  1. //公钥加密
  2. func LockWithPublicKey(src []byte, pubKeyFile string) ([]byte, error) {
  3.     var err error
  4.     //将公钥文件中的公钥读出，得到使用pem编码的字符串
  5.     file, err := os.Open(pubKeyFile)
  6.     if err != nil {
  7.         return nil, err
  8.     }
  9.     defer file.Close()
  10.  
  11.     fileInfo, err := file.Stat()
  12.     if err != nil {
  13.         return nil, err
  14.     }
  15.  
  16.     buffer := make([]byte, fileInfo.Size())
  17.     _, err = file.Read(buffer)
  18.     if err != nil {
  19.         return nil, err
  20.     }
  21.     //将得到的字符串解码
  22.     block, _ := pem.Decode(buffer)
  23.  
  24.     //使用x509将编码之后的公钥解析出来
  25.     pubInner, err := x509.ParsePKIXPublicKey(block.Bytes)
  26.     if err != nil {
  27.         return nil, err
  28.     }
  29.  
  30.     publicKey := pubInner.(*rsa.PublicKey)
  31.  
  32.     //使用得到的公钥通过rsa进行数据加密
  33.     encryptBytes, err := rsa.EncryptPKCS1v15(rand.Reader, publicKey, src)
  34.  
  35.     return encryptBytes, nil
  36. }
  1. //私钥解密
  2. func UnlockWithPrivateKey(src []byte, privateKeyFile string) ([]byte, error) {
  3.     //将私钥文件中的私钥读出，得到使用pem编码的字符串
  4.     file, err := os.Open(privateKeyFile)
  5.     if err != nil {
  6.         return nil, err
  7.     }
  8.     defer file.Close()
  9.  
  10.     fileInfo, err := file.Stat()
  11.     if err != nil {
  12.         return nil, err
  13.     }
  14.     size := fileInfo.Size()
  15.     buffer := make([]byte, size)
  16.     _, err = file.Read(buffer)
  17.     if err != nil {
  18.         return nil, err
  19.     }
  20.     //将得到的字符串解码
  21.     block, _ := pem.Decode(buffer)
  22.  
  23.     //使用x509将编码之后的私钥解析出来
  24.     privateKey, err := x509.ParsePKCS1PrivateKey(block.Bytes)
  25.     if err != nil {
  26.         return nil, err
  27.     }
  28.  
  29.     //使用得到的私钥通过rsa进行数据解密
  30.     decryptBytes, err := rsa.DecryptPKCS1v15(rand.Reader, privateKey, src)
  31.  
  32.     return decryptBytes, nil
  33. }

使用以上加解密方法：

  1. //测试RSA非对称加解密信息，公钥加密，私钥解密
  2. func TestRSA() {
  3.     //生成钥匙对
  4.     err := myRSA.GenerateKey(4096)
  5.     if err != nil {
  6.         fmt.Println(err)
  7.     }
  8.  
  9.     srcInfo := "GO 密码学 —— RSA非对称加解密测试"
  10.  
  11.     //公钥加密
  12.     encryptBytes, err := myRSA.LockWithPublicKey([]byte(srcInfo), myRSA.PUBLICFILE)
  13.     if err != nil {
  14.         fmt.Println(err)
  15.     }
  16.  
  17.     //私钥解密
  18.     decryptBytes, err := myRSA.UnlockWithPrivateKey(encryptBytes, myRSA.PRIVATEFILE)
  19.     if err != nil {
  20.         fmt.Println(err)
  21.     }
  22.  
  23.     fmt.Println("测试非对称加密结果：")
  24.     fmt.Println("元数据：", srcInfo)
  25.     encryptHex := hex.EncodeToString(encryptBytes)
  26.     fmt.Println("公钥加密数据：", encryptHex)
  27.     fmt.Println("私钥解密数据：", string(decryptBytes))
  28.  
  29. }
  30.  
  31. //首先会在规定的目录生成钥匙对文件：privateKey.pem、publicKey.pem
  32.  
  33. OUTPUT:
  34. 测试非对称加密结果：
  35. 元数据： GO 密码学 —— RSA非对称加解密测试
  36. 公钥加密数据： 582a4c0a2acdfb61cf2ee28bf6e85696b11415c5d84b515548268d15789752da50cc82dade81062bdbaccfeee227120eaf0cf4fcc46d174ccd1187a0a1318c987cc5f722bc8abeb9f425d3b890d6842dcda6731e9527528e9bdbbbe84220d972fb07049c1b7c5615731d5b61b148f42800d7c30ef5812da80d7b54bdea1ef93388d4eab33ccccb518da205672e3e9d9a2196b41cb000fc53c21e6a75f34ba2d5d941aac4f6cec9cdfd2ed443fe3207f32d636b4973ed94cc9d12362c55e399eea8163f253210ac8ff05b456046e643bdc26ca50648c2337b56399b5f4296903ca58fb0149fbbfb4ecf9c88d7d8b0beb2e0ea60fa2d3df2b7ffd0987259e720627f7f51070412a2d1e4da75c3dc7de2b9010b3f45e7b40c4f681621fd5aa686081e91fc00d578c0b7c8c41738c3d9b7655abc9963fd2d72f4006d0ad0af4e6e832868296fbe36098c8f226c6bc4557250039e6d631234bf7dabf7df9352d0b42e04cce8dc0d24961e927b996b99d87cf786cc48e865e4c093fc65f5fc047fea2141e5fc3648ae30ef7fc51837e4494954d7535512109ed7ed59e3fbf4e39b1e38a0bef1a771bcba656e77e1d6e522bf813cbf11715e1e781dd0e99f1c8ed5dce856ef1468e3a519c191c476ab778147a6ea9a6c311a9bf17beca2d80712180564d0986c6d02022e3640b8128f1cc4ea473aec79f5c7bd865b4de5c9e33cd9909d
  37. 私钥解密数据： GO 密码学 —— RSA非对称加解密测试
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/代码探险家/article/detail/854020
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号