devbox
代码领袖开发者
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

经典的十种排序算法 C语言版_c语言排序

作者：代码领袖开发者 | 2024-02-06 13:49:51

赞

踩

c语言排序

经典的十种排序算法(C语言版)

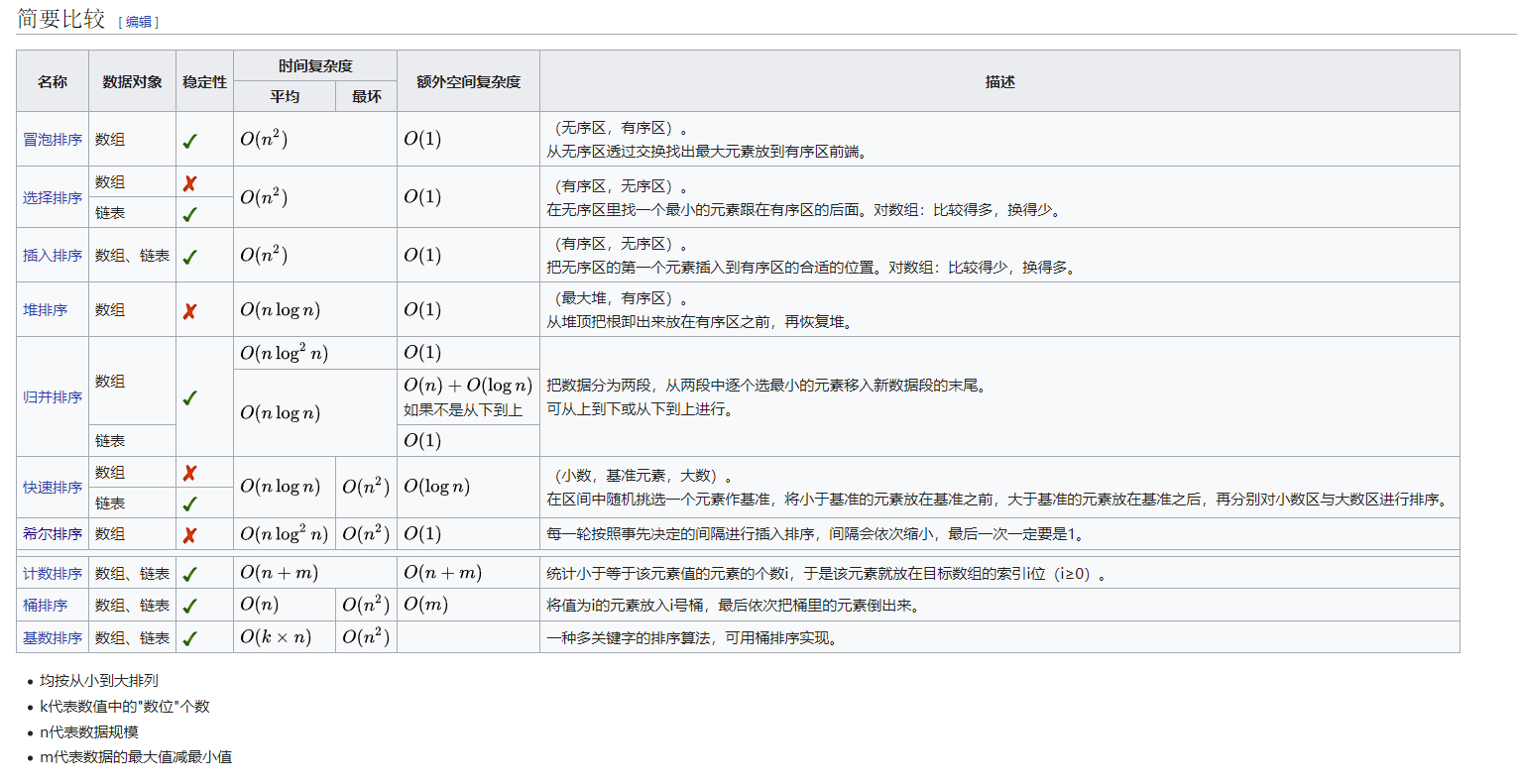
1.冒泡排序

冒泡排序的特点

​ 一趟一趟的比较待排序的数组，每趟比较中，从前往后，依次比较这个数和下一个数的大小，如果这个数比下一个数大，则交换这两个数，每趟比较后，数组的末尾总会变成目前未有序的数组中最大的数，重复每趟比较，只不过每趟的最后一个最大的数就不需要再次比较了，持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
​ 故可以创立一个标志位，如果这趟比较没有交换出现，则表示该数组已经有序，则可以提前结束循环。
​ 最坏的情况是所有元素都是逆序排列的，此时的时间复杂度是O(n^2)。
​ 最好的情况是所有元素都是顺序排列的，此时的时间复杂度是O(n)。
​ 冒泡排序的平均时间复杂度为O(n^2)。空间复杂度为O(1)，冒泡排序是稳定的排序。

冒泡排序的代码
#include<stdio.h>
void BubbleSort(int arr[],int len)
{
    //使用标志位flag 表示该趟比较有无交换元素
    int flag;
    for(int i=0; i<len-1; i++)
    {
        flag = 0;
        for(int j=0; j<len-i-1; j++)
        {
            //如果前面的元素大于后面的元素，交换这两个元素
            if(arr[j]>arr[j+1])
            {
                int temp = arr[j+1];
                arr[j+1] = arr[j];
                arr[j] = temp;
                flag = 1;
            }
        }
        //如果flag为0，表示数组已经有序，不需要再进行交换
        if(flag == 0)
        {
            break;
        }
    }
}

int main()
{
    //需要冒泡排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    BubbleSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40

2.选择排序

选择排序的特点

​ 一趟一趟的比较待排序的数组，每趟比较中，先把第一个数当做最小的数，记录位置，从前往后，依次比较这个数和下一个数的大小，如果这个数比下一个数大，记录更小的数的位置，每趟比较后，总会找出未排序的数组的最小值的位置，把这个数和第一个数交换，重复每趟比较，只不过每趟的第一个最小的数就不需要再次比较了，持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
​ 无论元素的排列顺序是什么样的，此时的时间复杂度都是O(n^2)，使用选择排序，数组元素越少越好。
​ 选择排序的平均时间复杂度为O(n^2)。空间复杂度为O(1)，选择排序是不稳定的排序。

选择排序的代码
#include<stdio.h>
void SelectSort(int arr[],int len)
{
    int temp;
    for(int i=0; i<len; i++)
    {
        //先把未排序的第一个元素拟为最小值
        temp = i;
        for(int j=i+1; j<len; j++)
        {
            //如果之前最小的元素大于后面的某个元素，将位置更新为更小的值
            if(arr[j]<arr[temp])
            {
                temp=j;
            }
        }
        //把未排序的第一个元素和找到的最小值进行交换 如果第一个元素就是最小值 就不交换了
        if(i!=temp)
        {
            int tem = arr[i];
            arr[i] = arr[temp];
            arr[temp] = tem;
        }
    }
}

int main()
{
    //需要选择排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    SelectSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39

3.插入排序

插入排序的特点

​ 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。就是选择一个元素，从后往前扫瞄，并依次交换相邻的元素，看这个元素放在哪个位置时，已排序对面加上这个元素是有序的，循环这个过程，最后得到有序的序列。

​ 最坏的情况是所有元素都是逆序排列的，此时的时间复杂度是O(n^2)。
​ 最好的情况是所有元素都是顺序排列的，此时的时间复杂度是O(n)。
​ 插入排序的平均时间复杂度为O(n^2)。空间复杂度为O(1)，插入排序是稳定的排序。

插入排序的代码
#include<stdio.h>
void InsertionSort(int arr[], int len)
{
    int j,key;
    //从第二个元素向前开始排序
    for (int i=1; i<len; i++)
    {
        //把该元素存下来
        key = arr[i];
        j=i-1;
        //从后往前挪动元素，直到前面的元素比该需要排序的元素小或者等于结束挪动
        while((j>=0) && (arr[j]>key))
        {
            //依次把前面的元素向后移动一位
            arr[j+1] = arr[j];
            j--;
        }
        //此时赋值给空缺出来的数组位置
        arr[j+1] = key;
    }
}

int main()
{
    //需要插入排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    InsertionSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36

4.希尔排序

希尔排序的特点

​ 是插入排序的一种更高效的改进版本。

​ 使用分组的方法简化插入排序比较和交换的次数。

希尔排序的步骤

​ 先使用一个gap，标记为排序的距离，一般是数组长度/2，然后按距离分为若干个分组，对于每一个分组，则在分组内使用插入排序。然后再把gap除2，循环上述操作，直到gap等于1，此时再执行一次交换排序。
​ 最坏的情况，此时的时间复杂度是O(n2)到O(n1.3) 不定，和选择gap的长度和具体的分组元素内容有关。
​ 希尔排序的平均时间复杂度为O(n(lgn)^2)。空间复杂度为O(1)，希尔排序虽然是一种插入排序但是希尔排序是不稳定的排序。

希尔排序的代码
#include<stdio.h>
void ShellSort(int arr[], int length)
{
    int k;
    int temp;	//希尔排序是在插入排序的基础上实现的,所以仍然需要变量来缓存数据
    //对于分组的步长 第一个分组是 长度/2的分组
    //后续分组长度都是前一个分组长度的一半
    //gap是分组的距离 该循环调整分组的距离
    for(int gap=length/2; gap>0; gap=gap/2)
    {
        //遍历每一个分组 得到分组的第一个元素的位置
        for(int i=0; i<gap; i++)
        {
            //遍历出该分组的每一个元素的位置
            for(int j=i; j<length; j=j+gap)
            {
                //对该分组进行单独一次的插入排序
                if(arr[j] < arr[j - gap])
                {
                    temp = arr[j];	//存入缓存数据
                    k = j - gap;
                    while(k>=0 && arr[k]>temp)
                    {
                        arr[k + gap] = arr[k];
                        k = k - gap;
                    }
                    arr[k + gap] = temp;
                }
            }
        }
    }
}
int main()
{
    //需要希尔排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    ShellSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45

5.归并排序

归并排序的特点

​ 是建立在归并操作上的一种有效的排序算法，算法的核心思想是采用分治法。

归并排序的步骤
  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针达到序列尾；
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

归并排序在任何时候时间复杂度都是O(nlgn)，空间复杂度都是O(n)，归并排序需要使用malloc函数进行内存分配，排序的数组不可超出内存大小，归并排序是稳定排序。

归并排序的代码
#include <stdio.h>
int min(int x, int y) {
    return x < y ? x : y;
}
void MergeSort(int arr[], int len) {
    int *a = arr;
    int *b = (int *) malloc(len * sizeof(int));
    int seg, start;
    //把数组分成几个小数组
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg * 2) {
            int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}
int main()
{
    //需要归并排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    MergeSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47

6.快速排序

快速排序的特点

​ 算法的核心思想是挑出一个元素作为基准。

快速排序的步骤
  1. 从数列中挑出一个元素，称为 “基准”（pivot）;
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

快速排序在最坏情况下时间复杂度是O(n^2),一般情况下的时间复杂度是O(nlgn)，空间复杂度是O(lgn)，快速排序是不稳定的排序。

快速排序的代码
#include <stdio.h>
//交换算法 通过指针交换两个数
void swap(int *x, int *y) {
    int t = *x;
    *x = *y;
    *y = t;
}

void QuickSortRecursive(int arr[], int start, int end) {
    if (start >= end)
        return;
    int mid = arr[end];
    int left = start, right = end - 1;
    while (left < right) {
        while (arr[left] < mid && left < right)
            left++;
        while (arr[right] >= mid && left < right)
            right--;
        swap(&arr[left], &arr[right]);
    }
    if (arr[left] >= arr[end])
        swap(&arr[left], &arr[end]);
    else
        left++;
    if (left)
        QuickSortRecursive(arr, start, left - 1);
    QuickSortRecursive(arr, left + 1, end);
}

void QuickSort(int arr[], int len) {
    QuickSortRecursive(arr, 0, len - 1);
}
int main()
{
    //需要归并排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    QuickSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45

7.堆排序

堆排序的特点

​ 是建立在堆操作上的一种有效的选择排序算法，算法的核心思想是构建大顶堆或者小顶堆，并使堆有序，对于大顶堆来说：随意选取某个结点，该结点的值大于左孩子、右孩子的值，可是左右孩子的值没有要求。

堆排序的步骤

1.首先将待排序的数组构造成一个大顶堆，此时，整个数组的最大值就是堆结构的顶端。

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1。

3.将剩余的n-1个数再构造成大顶堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组。

堆排序时间复杂度是O(nlgn)，空间复杂度是O(1)，堆排序是不稳定的排序。

堆排序的代码
#include <stdio.h>

//交换算法 通过指针交换两个数
void swap(int *a, int *b) {
    int temp = *b;
    *b = *a;
    *a = temp;
}

//大顶堆化，使其变成类似于完全二叉树的大顶堆
void MaxHeapify(int arr[], int start, int end) {
  // 建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { // 若子节点指标在范围内才做比较
        if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比较两个子节点大小，选择最大的
            son++;
        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函数
            return;
        else { // 否则交换父子内容再继续子节点和孙节点比较
            swap(&arr[dad], &arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

//初始化一个大顶堆，并调整节点的值
void HeapSort(int arr[], int len) {
    int i;
    // 初始化，i从最后一个父节点开始调整
    for (i = len / 2 - 1; i >= 0; i--)
        MaxHeapify(arr, i, len - 1);
    // 先将第一个元素和已排好元素前一位做交换，再重新调整，直到排序完毕
    for (i = len - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);
        MaxHeapify(arr, 0, i - 1);
    }
}


int main()
{
    //需要堆排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址进行排序
    HeapSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54

8.计数排序

计数排序的特点

​ 是建立在数组线性操作上的一种有效的排序算法，算法的核心思想是把要排序数组的值(value)作为另一个数组的键(key)，读取前一个数组的值为后一个数组的键对于的值+1，最后依序输出。

计数排序的步骤

1.先排序数组的值(value)作为另一个数组的键(key)。

2.读取前一个数组的值为后一个数组的键对应的值+1。

3.从小到大扫描另一个数组，输出一个非零值的键，键对应值就-1直到该键对应的值为0。

计数排序时间复杂度是O(n+k)，空间复杂度是O(n+k)，要注意数字的大小，如果排序大数就不推荐使用计数排序，计数排序是稳定的排序。

计数排序的代码
#include <stdio.h>
#include<stdlib.h>

//定义一个可以返回数组首元素指针的计数排序
int *CountSort(int arr[], int len,int max)
{
    //动态分配一个数组 大小为要排序数组中最大的数字
    int *b = (int *) malloc(max * sizeof(int));
    //把动态分配的数组全部置为0
    for (int i = 0; i < max; i++)
    {
        b[i] = 0;
    }
    //把要排序的数组的值为动态分配数组的键对应的值+1
    for(int i=0; i<len; i++)
    {
        b[arr[i]]++;
    }
    //返回动态分配的数组
    return b;
}

int main()
{
    //需要计数排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //把第一个数作为最大值
    int max = arr[0];
    //遍历找到最大值
    for(int i=0; i<9; i++)
    {
        if(max<arr[i])
        {
            max = arr[i];
        }
    }
    //传入数组arr的首地址和arr中的最大值进行排序 并接收返回数组
    int *arr1 = CountSort(arr,sizeof(arr)/sizeof(int),max);
    //排序完成后顺序输出排序结束后的arr数组
    //从小到大扫描另一个数组，输出一个非零值的键，键对应值就-1直到该键对应的值为0
    for(int i=0; i<=max; i++)
    {
        if(arr1[i]!=0)
        {
            while(arr1[i])
            {
                printf("%d ",i);
                arr1[i]--;
            }
        }
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53

9.桶排序

桶排序的特点

​ 是基于计数排序的一种节约空间占用的排序算法，算法的核心问题是设定一个函数K，使需要排序的N个元素经过函数K的变换，映射到M个桶里面。

桶排序的步骤

1.选定一个合理范围的函数K作为映射关系。

2.把待排序序列中的数据N根据函数映射方法K分配到若干个桶M中，在分别对各个桶进行排序，最后依次按顺序取出桶中的数据。

桶排序时间复杂度是O(n+k)，空间复杂度是O(n+k)，适用于数据分配均匀，数据比较大，相对集中的情况。桶排序是稳定的排序。

桶排序的代码
#include <stdio.h>
#include<stdlib.h>
void SelectSort(int arr[],int len)
{
    int temp;
    for(int i=0; i<len; i++)
    {
        //先把未排序的第一个元素拟为最小值
        temp = i;
        for(int j=i+1; j<len; j++)
        {
            //如果之前最小的元素大于后面的某个元素，将位置更新为更小的值
            if(arr[j]<arr[temp])
            {
                temp=j;
            }
        }
        //把未排序的第一个元素和找到的最小值进行交换 如果第一个元素就是最小值 就不交换了
        if(i!=temp)
        {
            int tem = arr[i];
            arr[i] = arr[temp];
            arr[temp] = tem;
        }
    }
}
void BucketSort(int arr[], int len){
    //把两个桶初始化
    //一个桶最多可以存放len个元素 防止最坏的情况发生
    int *arr1=(int *)malloc(sizeof(int)*len);
    int *arr2=(int *)malloc(sizeof(int)*len);
    int count1=0,count2=0;
    //对于变化K arr[i]/10 如果值为0 表示是个位数 放到桶子1 如果值不为0 表示不是个位数 放到桶子2 统计两个桶子里面元素的多少
    for(int i=0; i<len; i++){
        if((arr[i]/10)==0){
        //printf("arr[i] = %d,arr[i]/10 = %d \n",arr[i],arr[i]/10);
        arr1[count1]=arr[i];
        count1++;
        }else{
            //printf("arr[i] = %d,arr[i]/10 = %d \n",arr[i],arr[i]/10);
            arr2[count2]=arr[i];
            count2++;
        }
    }
   // printf("%d %d",count1,count2);
    //对桶子1 和 桶子2 同时进行选择排序
    SelectSort(arr1,count1);
    SelectSort(arr2,count2);
    //依次输出两个桶子中的元素
    for(int i=0; i<count1; i++)
    {
            printf("%d ",arr1[i]);
    }
    for(int i=0; i<count2; i++)
    {
            printf("%d ",arr2[i]);
    }
}


int main()
{
    //需要桶排序的数组
    int arr[]= {811,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址和arr中的最大值进行排序 并接收返回数组
    BucketSort(arr,sizeof(arr)/sizeof(int));
    return 0;
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69

10.基数排序

基数排序的特点

​ 基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。

基数排序的步骤

1.选定一个合理范围的函数K作为映射关系。

2.按个位开始往最高位开始划分桶，对每个桶的元素进行排序，再合并，再按位归并。

基数排序时间复杂度是O(n*k)，空间复杂度是O(n+k)，适用于数据分配均匀，数据比较大，相对集中的情况。桶排序是稳定的排序。

基数排序的代码
#include <stdio.h>
#include<stdlib.h>
void RadixSort(int *a, int n)
{
    int i, b[9], m = a[0], exp = 1;

    for (i = 1; i < n; i++)
    {
        if (a[i] > m)
        {
            m = a[i];
        }
    }

    while (m / exp > 0)
    {
        int bucket[10] = { 0 };

        for (i = 0; i < n; i++)
        {
            bucket[(a[i] / exp) % 10]++;
        }

        for (i = 1; i < 10; i++)
        {
            bucket[i] += bucket[i - 1];
        }

        for (i = n - 1; i >= 0; i--)
        {
            b[--bucket[(a[i] / exp) % 10]] = a[i];
        }

        for (i = 0; i < n; i++)
        {
            a[i] = b[i];
        }

        exp *= 10;
    }
}


int main()
{
    //需要基数排序的数组
    int arr[]= {1,1,4,5,1,4,19,19,810};
    //传入数组arr的首地址和arr中的最大值进行排序 并接收返回数组
    RadixSort(arr,sizeof(arr)/sizeof(int));
    //排序完成后顺序输出排序结束后的arr数组
    for(int i=0; i<9; i++)
    {
        printf("%d ",arr[i]);
    }
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号