图像的DCT算法_图像dct

一，背景介绍
DCT，即离散余弦变换，常用图像压缩算法，步骤如下
1）分割，首先将图像分割成8x8或16x16的小块；
2）DCT变换，对每个小块进行DCT变换；
3）舍弃高频系数（AC系数），保留低频信息（DC系数）。高频系数一般保存的是图像的边界、纹理信息，低频信息主要是保存的图像中平坦区域信息。
4）图像的低频和高频，高频区域指的是空域图像中突变程度大的区域（比如目标边界区域），通常的纹理丰富区域。

二，图像
二维DCT变换就是将二维图像从空间域转换到频率域。形象的说，就是计算出图像由哪些二维余弦波构成
$$F=Af{A}^T$$
$$A(i,j)=c(i)cos[\frac{(j+0.5)\pi }{N}i]$$

其中F就是变换得到的系数，f是图像的像素值，A是转换矩阵，其中i为二维波的水平方向频率，j为二维波的垂直方向频率，取值范围都是0-(N-1)，N是图像块的大小，
c ( i ) = { 1 N , i = 0 2 N , i ≠ 0 c(i)=\left\{

$$\begin{array}{rcl} \sqrt{\frac{1}{N}}, & & {i =0}\\ \sqrt{\frac{2}{N}}, & & {i \neq{0}}\\ \end{array}$$ \right. c(i)=⎩⎨⎧​N1​ ​,N2​ ​,​​i=0i​=0​
1）求出转换矩阵A；
2）利用转换矩阵A，转换到频域，即由图像 f 得到系数矩阵F。

三，Matlab实现图像块DCT变换

clc;clear;
f = (rand(4,4)*100); % 生成4x4块
% 1，根据公式，生成转换矩阵A
for i=0:3
    for j=0:3
        if i == 0
            c = sqrt(1/4);
        else
            c = sqrt(2/4);
        end
        A(i+1, j+1) = c * cos( (j + 0.5)* pi * i / 4 ); % 生成转换矩阵
    end
end

% 2，利用转换矩阵A，进行转换
dct_my = A*f*A'; % 转换
dct_matlab = dct2(f); % matlab自带函数转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

结果：

f =

   89.0903   14.9294   81.4285   19.6595
   95.9291   25.7508   24.3525   25.1084
   54.7216   84.0717   92.9264   61.6045
   13.8624   25.4282   34.9984   47.3289


dct_my =

  197.7977   21.3312    5.8547   40.7995
   10.7399   48.3374   21.6041   46.3630
  -34.4348  -18.4205    0.7236   18.6270
   51.2061  -20.9533  -41.4148    8.2377


dct_matlab =

  197.7977   21.3312    5.8547   40.7995
   10.7399   48.3374   21.6041   46.3630
  -34.4348  -18.4205    0.7236   18.6270
   51.2061  -20.9533  -41.4148    8.2377

>> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

四，DCT反变换
$$F=Af{A}^T$$
$$f=A^{-1}F(A^T{)}^{-1}$$
A是正交矩阵，所以有$A^T=A^{-1}$,所以求得：
$$f=A^{T}FA$$
五，Matlab实现DCT反变换
基于前面得到的转换矩阵A，则DCT反转换后面加一行代码即可：$f\_convert=A^{\prime }FA$

clc;clear;
f = (rand(4,4)*100)； % 生成4x4块
for i=0:3
    for j=0:3
        if i == 0
            c = sqrt(1/4);
        else
            c = sqrt(2/4);
        end
        A(i+1, j+1) = c * cos( (j + 0.5)* pi * i / 4 );
    end
end

dct_my = A*f*A'；
dct_matlab = dct2(f)；

f_convert = A'*dct_my*A；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

f =

   22.8977   53.8342   10.6653   81.7303
   91.3337   99.6135   96.1898   86.8695
   15.2378    7.8176    0.4634    8.4436
   82.5817   44.2678   77.4910   39.9783


dct_my =

  204.8538    1.1802    9.6825   -7.4417
   21.7177  -30.4859    8.3810  -50.0097
    1.8694   -9.0912   10.7823   -3.4473
 -121.8989  -10.6487   16.1003  -22.1974


dct_matlab =

  204.8538    1.1802    9.6825   -7.4417
   21.7177  -30.4859    8.3810  -50.0097
    1.8694   -9.0912   10.7823   -3.4473
 -121.8989  -10.6487   16.1003  -22.1974


f_convert =

   22.8977   53.8342   10.6653   81.7303
   91.3337   99.6135   96.1898   86.8695
   15.2378    7.8176    0.4634    8.4436
   82.5817   44.2678   77.4910   39.9783

>> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

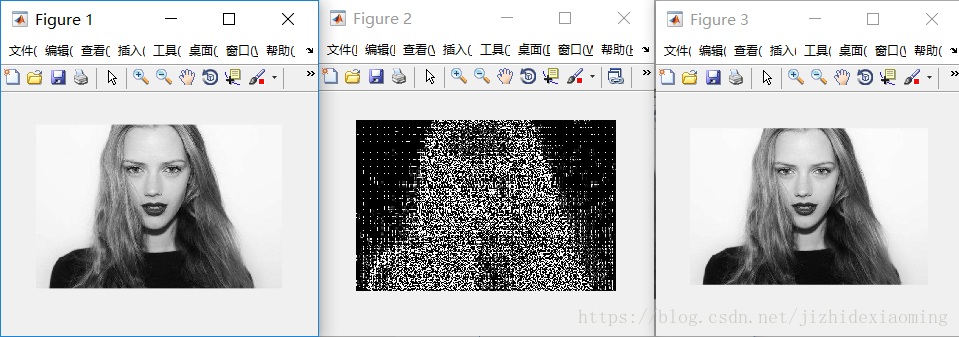
六，对图像进行DCT变换
效果图，分别是原图，所有dct系数小块组成图，反dct变换回来的图：

将图像分成8x8的小块，对每个小块依次进行dct变换，反变换回来时，也是依次处理每个小块。
matlab代码：

clc;clear;
img = rgb2gray(imread('D:\Code\Image\girl.jpg'));
figure, imshow(img); 

% 1，使图像行列为 8的倍数
[row,col] = size(img);
row = round(row/8) * 8; 
col = round(col/8) * 8;
img = imresize(img, [row, col]);

% 2，对图像块进行dct变换
img_dct = zeros(row, col); % 存放转换后的dct系数
for i=1:8:row-7
    for j=1:8:col-7
        img_block = img(i:i+7, j:j+7);
        dct_block = dct2(img_block); % 也可用刚才实现的(定义成一个函数即可)
        % imshow(dct_block); % 显示dct块
        img_dct(i:i+7, j:j+7) = dct_block;
    end
end
figure, imshow(img_dct); % 显示生成的dct系数

% 3，dct反变换
new_img = zeros(row,col);
for i=1:8:row-7
    for j=1:8:col-7
        dct_block = img_dct(i:i+7, j:j+7);
        img_block = idct2(dct_block); % 也可用刚才实现的(定义成一个函数即可)
        new_img(i:i+7, j:j+7) = img_block;
    end
end
figure,  imshow(mat2gray(new_img)); % 显示反变换回来的图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

放大后的dct系数块组成的图像：

1）发现每个小块的左上角，即一个DC系数，最亮，保存的是原图像低频信息，反应的是空域图像中平坦区域的信息；
2）小块的其他地方，即63个AC系数，保存的是高频信息，反应的是空域图像中的突变区域的信息；
3）对整个图像而言，背景区域是平坦区域，没有纹理信息，所以AC系数很小，而代表亮度信息的DC系数很大；
4）头发区域不仅含有亮度信息，纹理信息也丰富，所以AC系数值很大。

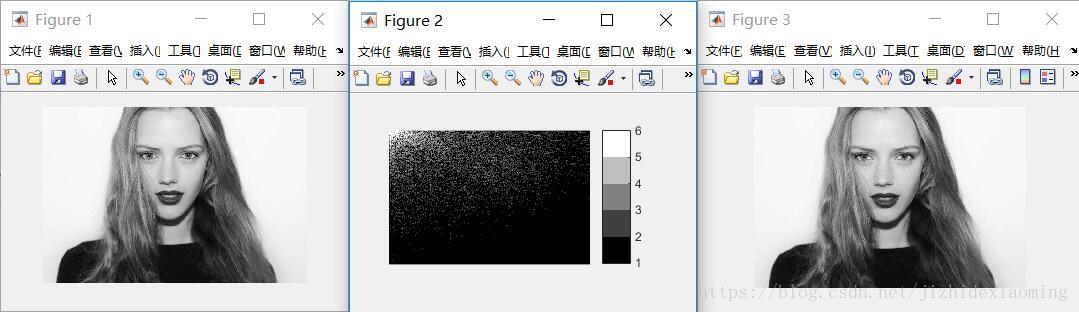
七，不分块，直接对整个图像DCT变换

clc;clear;
img = rgb2gray(imread('D:\Code\Image\girl.jpg'));
figure, imshow(img); 

% 1，对整个图像dct变换
dct_img = dct2(img);
figure, imshow(log(abs(dct_img)), colormap(gray(5)));
colorbar;

% 2，量化, 使得矩阵中小于0.1的值置为0，变得稀疏
dct_img(abs(dct_img)<0.1)=0; 

% 3，反变换回来
new_img = idct2(dct_img);
new_img = mat2gray(new_img);
figure, imshow(new_img);  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

效果图，分别是原图、整个图像变换后系数图、反变换得到的图：