- 1输电线路/杆塔/电力设施/安全穿戴等目标检测数据集_电力巡检设备状态指示灯数据集
- 2远程桌面与telnet连接_telnet链接服务器
- 3页面收录和关键词选取_收两千多页面,只有收录一百个关键词
- 4java linux 权限管理_Java 实现权限管理的两种方式
- 5Dubbo (五) ---------监控中心_dubbo 监控中心
- 6python 字符串(str)与列表(list)以及数组(array)之间的转换方法详细整理_python列表转成数组
- 7Linux的目录和文件管理_linux操作系统管理及应用实训2文件和目录的管理
- 8[PrimeVue] 自定义分类树(TreeTable)-分类树构建_primevue tree 缩进
- 92020-12-17_如下try-except的基本语法格式中,当执行<语句块1>时,不管产生了何种异常,一定会执
- 10解决ajax跨域无法共享session的问题_ajax session 空
Python 实战 | 进阶中文分词之 HanLP 词典分词(下)_no matching overloads found for com.hankcs.hanlp.s
赞
踩
更多内容点击查看Python 实战 | 进阶中文分词之 HanLP 词典分词(下)
Python教学专栏,旨在为初学者提供系统、全面的Python编程学习体验。通过逐步讲解Python基础语言和编程逻辑,结合实操案例,让小白也能轻松搞懂Python!
>>>点击此处查看往期Python教学内容
本文目录
一、引言
二、混淆矩阵
1. T-F-P-N
2. 准确率
3. 精确率
4. 召回率
5. F1值
三、中文分词场景的指标计算
1.分词场景的转换
2.代码实现
四、结束语
本文共8807个字,阅读大约需要23分钟,欢迎指正!
Part1 引言
上期文章Python 实战 | 进阶中文分词之 HanLP 词典分词(上),我们详细介绍了基于词典进行中文分词的三种切分规则,并且使用高性能分词器 HanLP 中的 DAT 分词器实现了词典分词。由于 HanLP 分词器的分词速度可以达到几千万字每秒,此时待分词的文本数据量已经不再是个问题,现在的问题是,面对庞大的分词结果数据集,我们要如何衡量分词结果的质量,总不能与正确的切分结果一 一核对吧?
接触过机器学习的朋友应该有了解,机器学习领域中已经有多种评估模型的指标,比如最基本的准确率,以及精确率、召回率、 值等等。实际上,在中文分词的场景中,我们一般使用后面这三个指标来衡量分词器的准确程度,下面我们将详细介绍这些指标是如何运用在中文分词场景中的,在此之前,我们首先需要理解混淆矩阵这个概念。
文本基于 HanLP 1.8.4 版本书写。
本文中所有 Python 代码均在集成开发环境 Visual Studio Code (VScode) 中使用交互式开发环境 Jupyter Notebook 中编写。
Part2 混淆矩阵
在进入中文分词任务之前,我们首先需要了解什么是混淆矩阵。混淆矩阵最初源于 1940 年代,当时被广泛用于信号检测理论中,用于描述信号存在和信号不存在这两种可能结果;后来在 1980 年代其开始盛行于机器学习领域,用于衡量和比较不同的预测模型。混淆矩阵是一个二维表格的形式(下文详细介绍),表格中的元素可以表示真实值与预测值之间的关系,在最常见的二分类问题中,混淆矩阵包含了四个元素,下面具体来看一下。
1. T-F-P-N
我们首先需要介绍一些概念。假设现在有一套设备检测系统,该系统识别出了一些合格的设备,此时识别的结果(合格为 Positive,不合格为 Negative)就可以分为以下两种情况:
-
系统识别是正确的,我们可以用 T(True)来表示正确。这时又分为两种:
a. 实际上是合格的设备,同时系统也检测为合格(P,Positive)的,这类情况就是 TP
b. 实际上是不合格的设备,同时系统也检测为不合格(N,Negative)的,这类情况就是 TN
-
系统识别是错误的,我们可以用 F(False)来表示错误。这时又分为两种:
a. 实际上是不合格的设备,但是系统检测为合格(P,Positive)的,这类情况就是 FP
b. 实际上是合格的设备,但是系统检测为不合格(N,Negative)的,这类情况就是 FN
这几个概念在刚开始接触时,可能会有些记不清,笔者在这里提供一个记忆的方式:先看第二个字母,比如 P 就表示做出了 Positive 的判断,N 表示做出了 Negative 的判断。再看第一个字母,如果为 T,则表示判断正确,比如 TN 在我们这个例子中表示系统做出了 Negative 的判断,并且这个判断是正确的,其他可以作类似理解。
通过上面这个例子可以理解,其实混淆矩阵就是通过原始类别和预测类别这两个维度将总体划分为四种情况,于是构建混淆矩阵如下:
| _ | 预测 | ||
| Positive | Negative | ||
| 实际 | Positive | TP | FN |
| Negative | FP | TN | |
在机器学习领域中这个图表就称为混淆矩阵,它是用来衡量分类结果的混淆程度的,P 通常理解为正例(即我们关注的样本),N 理解为负例,并且这四种情况有其对应的解释:
-
TP(True Positive,真阳):预测为 P,实际上也是 P
-
FP(False Positive,假阳):预测为 P,实际上是 N
-
TN(True Negative,真阴):预测为 N,实际上也是 N
-
FN(False Negative,假阴):预测为 N,实际上是 P
对于混淆矩阵,最重要的是知道每一个元素表示的含义,这些解释了解即可。注意一点,为了便于描述,下文统一将我们关注的样本称为正例,反之为负例。
2. 准确率
从字面意思理解,准确率(Accuracy)就是一个用于衡量结果的准确程度的值,它是机器学习领域最基本的评估指标之一,这也源于它的含义比较简单,容易计算。严格来说,准确率表示模型预测正确的样本占总样本的比例,结合上一节的概念,可以得到准确率的计算公式为
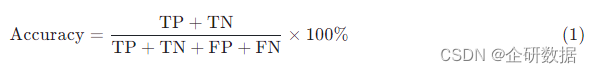
这个公式看起来很完美,也符合人们的直观印象,比如现在有 100 个参赛队伍,我们预测有 30 个队伍能进入下一个阶段的比赛,实际上的确进入了 30 个队伍,那么此时我们预测的准确率就是 100 %。在这个例子中,“能进入下一个阶段”是我们关注的正例,此时。可以看到,准确率评价的是整体的预测准确度,现在有一个问题是,如果我们的样本不均衡呢?
假设现在有一个用来预测信用卡欺诈的模型,我们有 1000 个样本,其中 10 个样本是欺诈行为,其余样本为正常行为,然后模型预测所有的样本交易都是正常的,也就是说模型完全忽略了欺诈行为,此时这个模型的准确率为 ,这个准确率非常的高,但仔细想一下,这是不合理的。在这个例子中,我们想要捕捉的是欺诈行为,但是这个模型并没有达到我们的目的,可以说效果很糟糕。所以,在样本不均衡的情况下,准确率这个指标是没有说服力的。我们需要更全面、公正的评价指标,如精确率、召回率和值。
3. 精确率
与预测整体的准确率不同,精确率是用来确保不会出错的。其表示的是模型预测为正且实际为正的样本占所有预测为正的样本的比例,简单来说,精确率是从预测的角度,度量模型预测为正的样本中,有多少是真正的正样本,其计算公式为

精确率是一个更关注质量的指标,比如在刚才的预测信用卡欺诈的模型中,我们关注的欺诈行为没有一个被识别出来,此时这个模型的精确率为 0。如果说高准确率保证了整体的利益,那么高精确率保证了个体的利益,也就是说每一个需要关注的正例,都经过了严厉的“考验”。
4. 召回率
召回率表示的是所有实际为正的样本中,模型预测为正的样本所占的比例,简单来说,召回率是从实际样本的角度,度量实际为正的样本有多少被预测出来了。其计算公式为

召回率更关注找到正例,换句话说就是更加希望找到所有的正例,即便这其中有一些误判。在区分精确率和召回率的时候,只要记住两者分子是一样的(真阳的数量),而精确率的分母是预测为正的数量,召回率的分母是实际为正的数量。
5. F1值
一般情况下,精确率和召回率之间难以平衡,精确率高往往召回率会低,反之同理。此时就需要一个权衡,我们可不可以同时考虑这些指标,而不是必须选择其中的一个,这也是为了避免单一指标而导致结论错误。值就是一个综合性的指标,它同时考虑了精确率和召回率,在样本不平衡的时候尤其有用。其计算公式为

只有当精确率和召回率的值同时较高时,我们才能得到一个较高的值,这时可以说明我们的模型质量是较好的。
Part3 中文分词场景的指标计算
通常情况下,混淆矩阵针对的是预测数量与实际数量相等的情况,如上文例子中的预测参赛队伍或者预测信用卡欺诈行为,预测的样本数量始终都与实际相同,但是在中文分词场景中,分词结果与标准答案的词语数量未必是一致的。另外混淆矩阵针对的是分类问题,而中文分词实际并不是分类问题。因此,我们需要转换思维,让混淆矩阵可以应用于分词场景中。
1. 分词场景的转换
假设我们有一个长度为n的字符串,分词的结果为一串连续的词语,根据词语在原字符串中的位置可以记作区间[i,j](1≤i≤j≤n)。现在我们就可以将标准答案与实际分词结果定义为两个集合了,标准答案的所有词语区间构成集合 A,作为正例,集合 A 之外的所有区间构成另一个集合(A 的补集),作为负例。同理,实际分词结果的所有区间构成集合 B。为了便于理解,我们对“这项研究在中国人民大学进行”这句话分词,得到如下表格:
| _ | 词语序列 | 集合 | 集合中的元素 |
| 标准答案 | 这项 研究 在 中国人民大学 进行 | A | [1,2],[3,4],[5,5],[6,11],[12,13] |
| _ | |||
| 分词结果 | 这项 研究 在 中国人 民 大学 进行 | B | [1,2],[3,4],[5,5],[6,8],[9,9],[10,11],[12,13] |
| _ | |||
| 重合部分 | 这项 研究 在 中国人民大学 进行 | A∩B | [1,2],[3,4],[5,5],[12,13] |
从上表可以清楚的看到,标准答案与实际分词结果重合的部分就是集合 A 与集合 B 的交集(A∩B),它表示的是判为正例,实际也是正例的数量,其实这就是混淆矩阵中的元素 TP。类似的,还可以得到:

此时,就可以在中文分词场景中计算精确率、召回率以及 值这三个指标了,计算公式如下:

比如我们现在需要计算上表的分词准确度,根据公式得到:
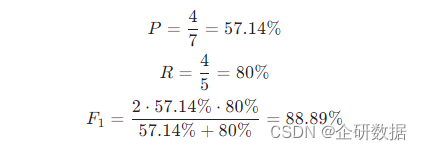
当待分词文本不止一句话时,先将词语区间存放在集合中,最后计算一次指标就可以了。
2. 代码实现
现在就需要使用代码实现上文的思路了,我们希望传入一个标准答案的文件路径和一个实际分词结果的文件路径,函数就可以输出精确率、召回率和 三个指标值。需要注意一点,两份文件内容应该是按行一 一对应的。
首先,我们需要将分词结果转换为区间形式,代码如下:
- # 导入需要使用的库
- import re
- from pyhanlp import *
-
- # 将分词结果转换为区间
- def seg_to_region(seg: str): # 传入的参数 seg 为字符串
- # 切分分词结果的规则
- pat = re.compile(r'\s+')
- # 用于存放集合的空列表
- region = []
- # 设置起始位置
- start = 0
- # 处理每一个词语,将其转换为区间(集合)
- for word in pat.split(seg.strip()):
- end = start + len(word)
- # 添加集合到 list 中
- region.append((start, end))
- # 更新起始位置
- start = end
- # 将列表转换为 set 类型
- return set(region)

可以留意到,在代码的循环语句部分,我们先通过seg.strip()对分词结果进行了处理,去除了两端的空格。这是因为如果两端有空格,程序会将两端的空格单独分出来一个区间,这会影响指标的计算结果。另外,在函数的返回值部分,使用了函数set()将列表转换为集合数据类型,这是因为在计算指标时集合可以进行运算(比如并集、交集等)。其他的内容就不再赘述了,代码中都有详细的说明。
现在我们传入上文得到的分词结果,来看一下输出内容是什么:
- seg_to_region('这项 研究 在 中国人 民 大学 进行')
-
- # 输出结果
- '''
- {(0, 2), (2, 4), (4, 5), (5, 8), (8, 9), (9, 11), (11, 13)}
- '''
可以看到输出结果为一个包含所有区间的集合,每一个区间也是以集合的形式存储。现在区间已经转换完成了,下一步就是计算分词准确度的指标。代码如下:
- # answ 为标准答案的文件路径;pred 为实际分词结果的文件路径
- def PRF_COUNT(answ, pred):
- A_size, B_size, A_inter_B_size = 0, 0, 0
- with open(answ, encoding='utf-8') as afile, open(pred, encoding='utf-8') as pfile:
- # a、p 为一 一对应的标准答案和实际分词结果
- for a, p in zip(afile, pfile):
- # A 为标准答案的集合
- A = seg_to_region(a)
- # B 为实际分词结果的集合
- B = seg_to_region(p)
- # 将结果先保存,最后计算一次指标
- A_size += len(A)
- B_size += len(B)
- A_inter_B_size += len(A & B) # A∩B 的集合大小
- P = A_inter_B_size / B_size * 100
- R = A_inter_B_size / A_size * 100
- # 返回三个指标:精确率、召回率、F1值
- return P, R, 2*P*R / (P+R)

实际使用中,我们通常是将分词结果写入文本文件(如txt文件)中,所以函数PRF_COUNT中需要传入的是存放结果的文件路径。
下面我们使用 SIGHAN05(第二届国际中文分词测评)提供的 MSR 语料库(微软亚洲研究院语料库)以及对应词典看一下运行结果如何。在此之前,需要先下载数据包,大家可以前往第二届国际中文分词评测[1]下载名为icwb2-data.zip的压缩文件,并将其放在 HanLP 的 data 路径下(在命令窗口输入hanlp -v可以找到 data 路径)

笔者建议将完整的解压文件放在一个新建的文件夹中,避免与其他文件放在一个文件夹下。解压后的文件如下:
MSR 语料库的词典位于icwb2-data/training/msr_training.utf8,待分词的语料位于icwb2-data/testing/msr_test.utf8,标准答案位于icwb2-data/gold/msr_test_gold.utf8中。我们的思路是先加载词典构造使用的分词器,然后对待分词语料进行分词,最后将分词结果与标准答案作比较计算出指标值。
- import re,os
- from pyhanlp import *
-
- # 数据包 icwb2-data 的路径(HANLP_DATA_PATH 为 HanLP 的 data 路径)
- DIR_PATH = os.path.join(HANLP_DATA_PATH, 'test', 'icwb2-data')
-
- MSR_DICT = os.path.join(DIR_PATH, 'gold', 'msr_training_words.utf8') # MSR 语料的词典路径
- MSR_TEST = os.path.join(DIR_PATH, 'testing', 'msr_test.utf8') # 待分词的语料
- MSR_OUTPUT = os.path.join(DIR_PATH, 'testing', 'msr_output.txt') # 实际分词结果的文件路径
- MSR_ANSW = os.path.join(DIR_PATH, 'gold', 'msr_test_gold.utf8') # 标准答案的文件路径
-
- # 构造分词器(这里使用 DoubleArrayTrieSegment 分词器)
- DoubleArrayTrieSegment = JClass('com.hankcs.hanlp.seg.Other.DoubleArrayTrieSegment')
- segment = DoubleArrayTrieSegment([MSR_DICT]) # 加载 MSR 语料的词典
- segment.enablePartOfSpeechTagging(True) # 开启词性标注
-
- # 对待分词文本进行分词,并将结果保存在文件 MSR_OUTPUT 中
- with open(MSR_TEST, encoding='utf-8') as seg_text, open(MSR_OUTPUT, 'w', encoding='utf-8') as output:
- for one_line in seg_text:
- output.write(' '.join(term.word for term in segment.seg(re.sub(r'\s+', '', one_line))))
- output.write('\n')
-
- # 输出返回结果
- print('P:%.2f R:%.2f F1:%.2f' % PRF_COUNT(MSR_ANSW, MSR_OUTPUT))
-
- # 结果如下
- '''
- P:91.68 R:95.57 F1:93.58
- '''

可以看到,HanLP 词典分词在 MSR 语料库上的精确率、召回率和 值均在 91% 以上,这个结果是较好的。再来对上面的代码作进一步的解释,这里使用的是 HanLP 中的双数组字典树分词器,并且开启了词性标注,这是为了可以识别数据和英文(上期文章提到过,HanLP 中这两块功能是同时开启或关闭的);接着,按行提取待分词文本,同时去除其中的空格符,这也是为了避免多余的空格导致结果不准确,然后将分词结果写入输出文件中;最后返回的指标值均保留两位小数。
实际上,基于混淆矩阵的准确度评估方法不止可以用于中文词典分词,其他的算法也是可以的。后续若有机会,我们也会向大家介绍。
Part4 结束语
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


