《PRML》学习笔记2.2——多项式分布和狄利克雷分布_多项式分布与迪利克雷分布

作者：你好赵伟 | 2024-03-06 02:24:58

踩

多项式分布与迪利克雷分布

上回讲完了伯努利分布、二项分布和Beta分布，以及从最大似然估计的非参数化思想和引入共轭先验，使得参数变成一个变量，建模求解的参数化方法两方面介绍了求解模型参数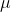 $\mu$ 的方法。没有读过的朋友可以参考：《PRML》学习笔记2.1——伯努利分布、二项分布和Beta分布，从贝叶斯观点出发

今天将为大家介绍两个更难理解的分布——多项式分布和狄利克雷分布。

1.多项式变量和多项式分布

伯努利分布的一个经典例子就是掷硬币，当你掷出去的时候，得到的结果只有正面朝上或者反面朝上两种可能，因此可以用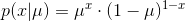 $p(x|\mu)=\mu^{x}\cdot(1-\mu)^{1-x}$ 进行建模。概率密度的表达式中，的取值只有两种情况——0或1，那么，这个建模方法就不适用于掷骰子了，毕竟骰子有6个面，对应着6种投掷结果。所以这时候就要将服从伯努利分布的变量进行扩展了。

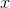
首先，使用一种方式来表达投掷骰子的结果，这里推荐的是"1-of-K"表示法，使用一个K维向量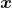 $\boldsymbol{x}$ 来表示状态，向量中一个元素 $x_k$ 等于1，其余元素为0，用来表示发生的是第k中情况：

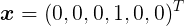
$\large \boldsymbol{x}=(0,0,0,1,0,0)^T$ (1)

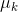
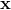
如果用参数 $\mu_k$ 表示 $x_k=1$ 的概率，那么 $\mathbf{x}$ 的分布为：

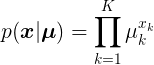
$\large p(\boldsymbol{x}|\boldsymbol{\mu})=\prod_{k=1}^{K}\mu_k^{x_k}$ (2)

因为 $\mu_k$ 代表的是一种情况的概率，所以 $\mu_k$ 满足

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/你好赵伟/article/detail/195574