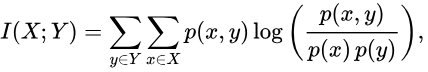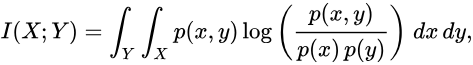NLP系列 3. 特征选择——TF-IDF原理以及利用其进行特征筛选_tf-idf文本分类特征选择

TF-IDF原理以及利用其进行特征筛选

原理

TF-IDF即term frequency - inverse document frequency, 词频-逆文本频率
TF词频: 容易理解, 频率高能够在一定程度上反应该词的重要性.
IDF逆文本频率: 若某一个词在所有文本中都出现, 或出现的频率过高, 则也有可能是虚词这种重要性不高却频率很高的词, 此时单纯依靠词频来判断词的重要性就不可靠了. 所以引入了IDF逆文本频率这一个量与TF共同判断词的重要性.
最简单的IDF的公式: $IDF(x)=log\frac{N}{N(x)}$
其中, N为文本总数, N(x)为该词出现的次数.
但是, 这个公式有一个问题, 当该词没有出现过的时候, N(x)=0, IDF(x)的分母为0, 就没有意义了.
所以进行平滑处理把上式变化为: $IDF(x)=log\frac{N+1}{N(x)+1}+1$

使用方法

使用jieba

(这一部分我在上一篇博客中也提到了)
参考 https://blog.csdn.net/u012052268/article/details/77825981#61__155 以及 https://github.com/fxsjy/jieba
jieba分词的官方Github上面就已经说明了支持TF-IDF

基于 TF-IDF 算法的关键词抽取
import jieba.analyse

• jieba.analyse.extract_tags(sentence, topK=20, withWeight=False, allowPOS=())
  sentence 为待提取的文本
  topK 为返回几个 TF/IDF 权重最大的关键词，默认值为 20
  withWeight 为是否一并返回关键词权重值，默认值为 False
  allowPOS 仅包括指定词性的词，默认值为空，即不筛选
• jieba.analyse.TFIDF(idf_path=None) 新建 TFIDF 实例，idf_path 为 IDF 频率文件

import jieba.analyse
import os
f=open('output.txt',"r")
news=''
for i in range(10):
    string=f.readline()
    news+=string
# 第一个参数：待提取关键词的文本
# 第二个参数：返回关键词的数量，重要性从高到低排序
# 第三个参数：是否同时返回每个关键词的权重
# 第四个参数：词性过滤，为空表示不过滤，若提供则仅返回符合词性要求的关键词
keywords = jieba.analyse.extract_tags(news, topK=20, withWeight=True, allowPOS=())
# 访问提取结果
for item in keywords:
    # 分别为关键词和相应的权重
    print(item[0], item[1])

# 同样是四个参数，但allowPOS默认为('ns', 'n', 'vn', 'v')
# 即仅提取地名、名词、动名词、动词
keywords = jieba.analyse.textrank(news, topK=20, withWeight=True, allowPOS=('ns', 'n', 'vn', 'v'))
# 访问提取结果
for item in keywords:
    # 分别为关键词和相应的权重
    print(item[0], item[1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

结果如下:

使用sklearn

方法一: 利用CountVectorizer和TfidfTransformery

先使用CountVectorizer进行向量化, 再使用TfidfTransformer进行预处理.

from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer
corpus=["I come to China to travel", 
    "This is a car polupar in China",          
    "I love tea and Apple ",   
    "The work is to write some papers in science"] 
vectorizer=CountVectorizer()
transformer=TfidfTransformer()
vector=vectorizer.fit_transform(corpus)
tfidf=transformer.fit_transform(vector)
print(tfidf)
1
2
3
4
5
6
7
8
9
10
11

结果如下:

方法二: 直接使用TfidfVectorizer

使用TfidfVectorizer完成向量化与TF-IDF预处理

from sklearn.feature_extraction.text import TfidfVectorizer
corpus=["I come to China to travel", 
    "The work is to write some papers in science"] 
tfidf2=TfidfVectorizer()
re=tfidf2.fit_transform(corpus)
print(re)
1
2
3
4
5
6

结果如下:

互信息的原理以及利用其进行特征筛选

定义

互信息是信息论中对变量之间相互依赖性的量度.

一般地，两个离散随机变量 X 和 Y 的互信息可以定义为：

其中 p(x,y) 是 X 和 Y 的联合概率分布函数，而 {\displaystyle p(x)} p(x) 和 {\displaystyle p(y)} p(y) 分别是 X 和 Y 的边缘概率分布函数。
在连续随机变量的情形下，求和被替换成了二重定积分：

其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数，而 {\displaystyle p(x)} p(x) 和 {\displaystyle p(y)} p(y) 分别是 X 和 Y 的边缘概率密度函数。
(摘自维基百科 https://zh.wikipedia.org/wiki/互信息)
互信息可以简单地理解为一个随机变量中包含另一个随机变量的的信息量.

使用方法

使用sklearn进行计算.

from sklearn.metrics import mutual_info_score
signals=[1,1,0,0,0]
labels_1=['a','a','b','b','b']
print(mutual_info_score(signals,labels_1))
labels_2=['a','a','a','a','b']
print(mutual_info_score(signals,labels_2))
1
2
3
4
5
6

输出结果:

0.6730116670092563
0.11849392256130009
1
2

互信息量大则说明上述signals与labels对应关系较好, signals与labels在更大程度上互相包含.
但是有可能会出现互信息量失效的情况.

from sklearn.metrics import mutual_info_score
signals=[1,1,0,0,0]
labels_1=['a','a','b','b','b']
print(mutual_info_score(signals,labels_1))
labels_2=['a','b','c','d','e']
print(mutual_info_score(signals,labels_2))
1
2
3
4
5
6

两个互信息输出结果相等

0.6730116670092563
0.6730116670092563
1
2

原因大致是

互信息虽然反映了指标（对于标签）的绝对表达能力（通过信息量来度量），但没有反映出指标集相对于标签集整体表达能力的真实减弱。
重点是互信息提供的是指标和标签之间的绝对信息量，而这在实践中随指标集和标签集的自身规模变化而变化，并不真实反映指标集相对于标签集整体的表达能力，要在实际数据中使用互信息挑选指标就很容易进坑了，难怪这个指标表现得时好时坏，并不稳定。
参考 https://www.douban.com/note/621588501/

标准化互信息

要对熵的整体大小标准化可以消除熵大小的影响.
需要针对 H(A) 和 H(B) 的整体大小标准化，以消除H(A)和 H(B) 大小的影响，这就是标准化互信息

使用sklearn.normal_mutual_info_score即可

from sklearn.metrics import normalized_mutual_info_score
signals=[1,1,0,0,0]
labels_1=['a','a','b','b','b']
print(normalized_mutual_info_score(signals,labels_1))
labels_2=['a','b','c','d','e']
print(normalized_mutual_info_score(signals,labels_2))
1
2
3
4
5
6

结果如下

1.0
0.6466572972441055
1
2

相关博客

https://blog.csdn.net/u013829973/article/details/79200879
这篇博客利用sklearn对特征选择进行了很充分的讲解, 值得一看.

参考链接

https://www.cnblogs.com/pinard/p/6693230.html
https://blog.csdn.net/u013710265/article/details/72848755
https://www.douban.com/note/621588501/
https://zh.wikipedia.org/wiki/互信息