精英反向学习与二次插值改进的黏菌优化算法ISMA(学习笔记_13)_反向学习机制求反向解

1.理论分析

1.SMA

• 优点：较强的全局探索能力
• 缺点：后期迭代震荡作用较弱，易陷入局部最优；收缩机制不强，收敛速度较慢；初始种群质量低，探索和开发过程难以平衡。

2.精英反向学习机制

• 反向学习OBL：

  • 先求当前解的反向解，再从当前解和反向解中选取最优解并更新个体。

  • 其研究指明反向解比当前解逼近最优解的概率高，有效增加算法种群的多样性和质量。

  • 针对反向学习生成的反向解可能比当前的搜索空间更难搜索到最优值的问题，提出EOBL。

• 精英反向学习EOBL：

  • 其他算法对于EOBL机制的应用：何庆等人采用 EBOL 方法初始化种群，增加了蜻蜓算法的种群多样性；方旭阳等人引入 EBOL 优化正余弦算法，避免个体盲目地向当前学习。
  • EBOL 机制利用精英个体相对普通个体而言携带更多有效信息的优势，首先通过种群中精英个体形成反向种群，再从反向种群和当前种群中选取优秀个体构成新的种群。

• 精英反向解公式：
  $$Xeij=\delta \times (lbj+ubj)－XEij$$

  • 参数说明：Xe 为精英反向解，XE为精英解，δ 是［0，1］上的随机值，XEij ∈［lbj，ubj］。

  • lbj = min( Xij ) ，ubj = max( Xij) ，lbj 和 ubj 分别为动态边界的下界和上界，min( Xij) 、max( Xij) 分别为第 j 维个体的最小值和最大值。动态边界解决了固定边界难以保存搜索经验的问题，有利于减少算法的寻优时间。

  • 如果精英反向解 Xeij 超过边界，利用随机生成的方式将其重置，重置方程如下:
    $$Xeij=rand(lbj，ubj)$$

• 效果：有利于提高黏菌种群多样性和种群质量，提升算法全局寻优性能与收敛精度。

3.二次插值方法

• 二次插值( quadratic interpolation，QI) 是一种局部搜索算子，它使用曲线来拟合二次函数的形状，以获得曲线极值点近似函数最优解。

• 其他算法对于QI的应用：

  • Sun 等人提出了二次插值改进的鲸鱼优化算法。
  • 廖列法等人提出二次插值改进的天牛须算法。
  • 王秋萍等人提出了二次插值改进的飞蛾火焰算法。

• QI：假设 X 和 Y 是 D 维问题中种群的两个随机位置，其中， X = ( x1，x2，…，xD ) ，Y = ( y1，y2，…，yD )，当前全局最优位置为Z = ( z1，z2，…，zD )，X、Y、Z 的适应度值分别为 F( X) 、F( Y) 、 F( Z)，则二次插值方法根据以下公式更新位置形成新个体nX = ( nx1，nx2，…，nxD ) 。
  
  其中：q = 1,2, …,D

• 效果：有利于增强算法局部开发能力，减少算法收敛时间，使算法跳出局部极值。

4.精英反向学习与二次插值改进的黏菌优化算法ISMA

• 仅采用精英反向学习改进的黏菌算法ESMA

  仅引入二次插值改进的黏菌算法QSMA

• 基本 SMA 采用随机初始化的方法初始化种群，没有先验知识，易导致黏菌种群多样性差的问题。

• 精英反向学习机制：

  • 融入 EBOL 策略的黏菌算法提高了初始化种群的多样性，增加了搜索空间，奠定了算法进行全局优化的基础。

  • 在每次迭代时，EBOL 策略可以产生远离局部极值点的反向解，指引黏菌算法跳出局部极值，增强算法全局搜索的能力。

  • EBOL策略采用动态边界的跟踪搜索模式将个体定位在逐步缩小的搜索区域中，提高黏菌算法的收敛精度和速度。

• 二次插值方法：

  • 提高黏菌算法局部探索和跳出局部极值点的能力；二次插值产生的新解可以增加黏菌种群的多样性。

  • 黏菌个体根据二次插值位置更新公式更新位置，在满足某个精度的条件下得到一个最优位置 nX。使其与目前全局最佳位置Z进行对比，取优作为新的全局最佳位置 Xb，具体操作如下：
    

2.ISMA流程图

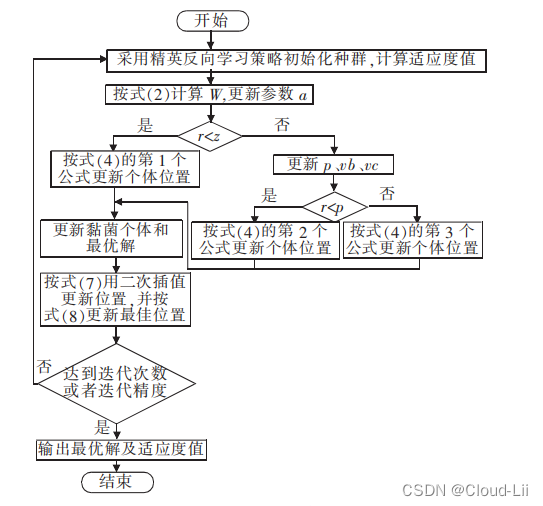
3.仿真实验

• 为了更好的验证 ISMA 算法性能，选取了 5 种算法进行对比：SMA、PSO、WOA、LSMA、HSMAAOA（论文中包括ChOA、BOA算法，但由于笔者还没有学习ChOA、BOA算法，故暂不加入实验，加入另一种SMA的改进算法HSMAAOA），这些算法被证实具有良好的寻优性能。为了更准确的验证所提算法与对比算法的优劣性，设定种群规模 N=30，维度 D=30，最大迭代次数 500 次，各算法独立运行 30 次。

• 选取最优值、最差值、平均值与标准差作为评价指标。其中，平均值与标准差越小，则证明算法的性能越佳。

• 例举几个测试函数的收敛曲线：中F3、F4（单峰函数）、F6、F7（多峰函数），F21（固定维多峰函数）结果显示如下：
  

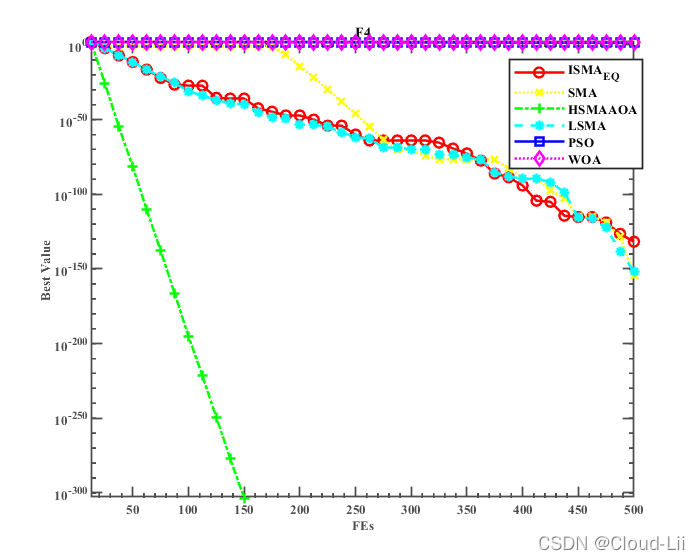
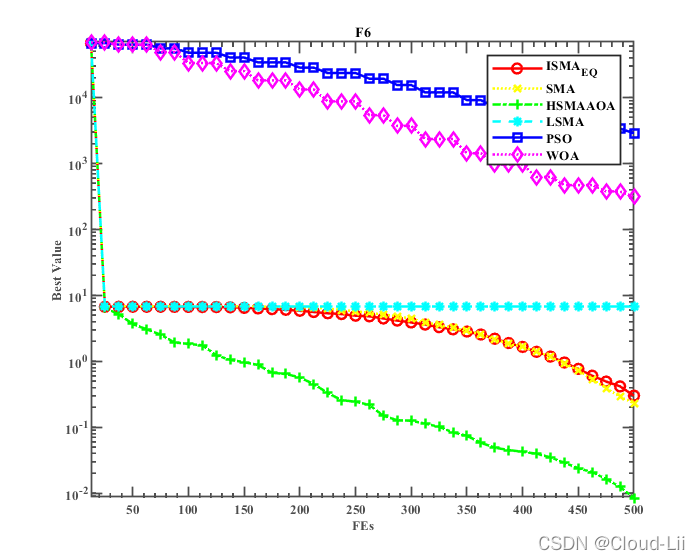
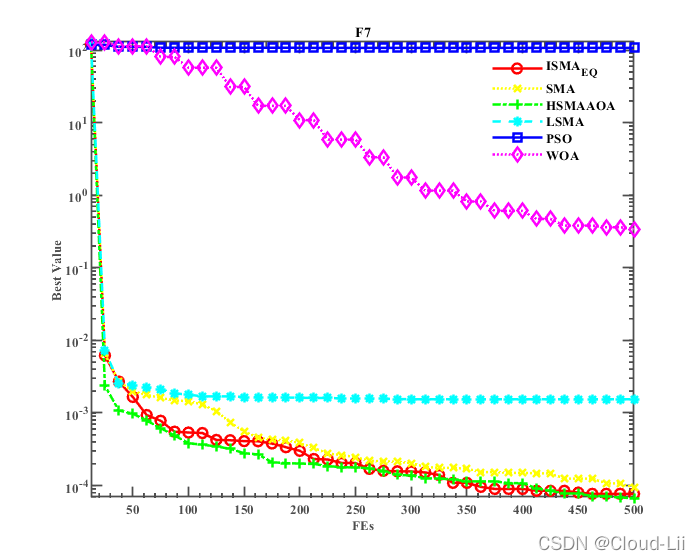
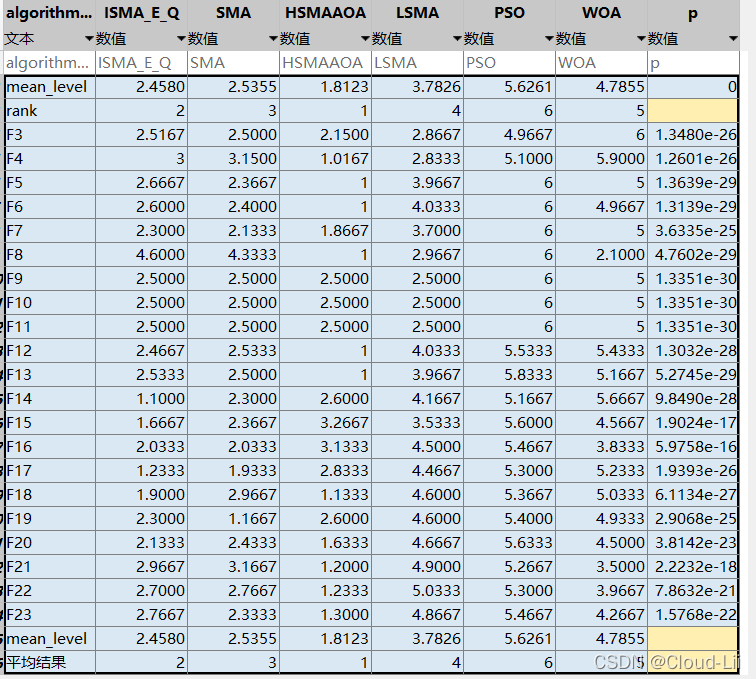
• 实验结果表明：结合两种改进策略较好地提升了黏菌算法的全局寻优性能、精度、速度以及鲁棒性。但其优化效果较HSMAAOA算法较弱。

4.参考文献

[1]郭雨鑫,刘升,张磊,黄倩.精英反向与二次插值改进的黏菌算法[J].计算机应用研究,2021,38(12):3651-3656.DOI:10.19734/j.issn.1001-3695.2021.02.0175.