LeetCode73：矩阵置零_给定一个 × n×m 的矩阵,如果一个元素为 0 0,则将其所在行和列的所有

题目：

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例：

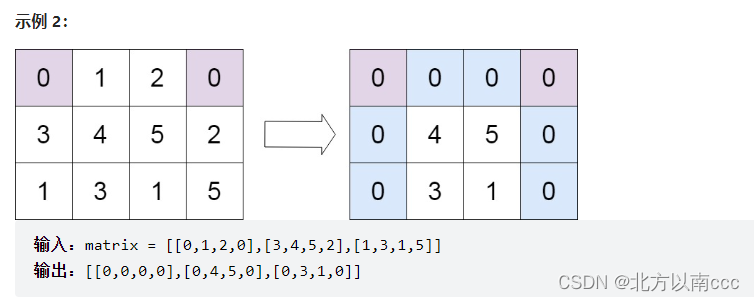
提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1

本道题的题目并不难理解，最重要的就是需要在原来的矩阵中进行修改

第一步先定义vector数组来记录0元素的横纵坐标

       vector<int> x;
        vector<int> y;

下一步利用两个for（）来把矩阵所有的元素遍历一遍。如果遇到0元素，就将横坐标push_back（）到x中，纵坐标push_back( )到y中。

        int m = matrix.size();
        int n = matrix[0].size();
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (matrix[i][j] == 0)
                {
                    x.push_back(i);
                    y.push_back(j);
                }
            }
        }

然后再用sort（）排序函数对x,y数组中的元素进行排序

        sort(x.begin(), x.end());
        sort(y.begin(), y.end());

然后最后一步就该在原矩阵中进行修改

利用for（）遍历所有的矩阵元素时

用binary_search( )二分查找i，j是否在x，y数组中出现过，返回true，则将其元素修改为0；

        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                bool ret = binary_search(x.begin(), x.end(), i);
                bool res = binary_search(y.begin(), y.end(), j);
                if (ret == true || res == true)
                {
                    matrix[i][j] = 0;
                }
            }
        }

ps：binary_search()必须是bool类型定义，而且查找方法是二分查找，所以必须是有序数组，这也是提前用sort（）函数的意图所在。

完整代码：

class Solution
{
public:
    void setZeroes(vector<vector<int>> &matrix)
    {
        vector<int> x;
        vector<int> y;
        int m = matrix.size();
        int n = matrix[0].size();
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (matrix[i][j] == 0)
                {
                    x.push_back(i);
                    y.push_back(j);
                }
            }
        }
        sort(x.begin(), x.end());
        sort(y.begin(), y.end());
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                bool ret = binary_search(x.begin(), x.end(), i);
                bool res = binary_search(y.begin(), y.end(), j);
                if (ret == true || res == true)
                {
                    matrix[i][j] = 0;
                }
            }
        }
    }
};

本道题的思路就是这样了。

欢迎各位读者的补充！