《信号与系统》解读 第3章 强大的傅里叶时域频域分析工具-4：傅里叶运算的5大主要特性_,通过比较结果的幅频特性曲线,验证连续时间傅里叶变换的频移特

前言：

傅里叶变换是属于“信号与系统”的“系统”部分，它是对输入的时域信号进行处理，然后得到频率信号。本质上是一种数学运算。

从傅里叶数学运算总体的效果上，傅里叶运算具有5大特性：

1. 线性特性

2. 共轭对称性

3. 时移特性/相移特性（时间t的平移）

4. 对偶/称特性

5. 频移特性

---

1. 线性特性

（1）图形表达

• 线性放大的乘法运算

时域信号的幅度放大，对应于频域信号幅度的放大。

• 线性相加的加法运算

时域信号的幅度相加，对应于相应频域信号幅度的相加。

（2）数学表达式

线性特性表明：多个时域信号累加后的频率特性，是单个时域信号傅里叶变换后的频率特性的累加。

这个特性非常重要，在解决实际问题是也很实用。

对于复杂的时域信号，可以先通过线性分解，把一个复杂的时域信号先分解成多个简单的时域信号，

然后对单个时域信号进行傅里叶运算，并把各自运算的结果进行累加，最后得到复杂的时域信号的傅里叶运算的频域信号。

（3）实际案例

---

2. 共轭对称性

“共轭”的这个词不很直观，其实共轭的本意是：两头牛背上的架子称为轭，轭使两头牛同步行走。

共轭即为按一定的规律相配的一对。通俗点说就是孪生。

共轭是针对复数而言的，如果两个复数的实部相等，其虚部为相反数，那么这两个复数就是共轭的。

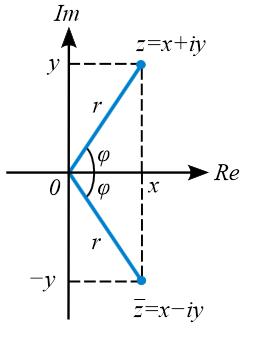
傅里叶变化的共轭特性是指：

（1）图形表达

（2）数学表达式

（3）实际案例

---

3. 时移特性/相移特性（时间t的平移）

（1）图形表达

从上图可以看出，时域信号在增加延时t0后，频率特性并没有发生变化，变化的是移动了一个在t0时间内相位，相位的大小为：ω*t0，体现在图中就是$\small e^{-jwt0}$.

（2）数学表达式

（3）实际案例

---

4. 对偶/称特性

（1）图形表达

• 情形1

这个特性相的相对比较简单，但其蕴含了的时域与频域最极端的两种情形！时间变化t趋于0和趋于无穷；谐波信号的频率趋于0和趋于无穷，各两种极端情形。

时域上瞬间变化的脉冲信号，体现在频率上，包含了所有频率值的谐波分量。

时域上永恒不变的直流信号，体现在频率上，占用频谱资源的0频，就频率大小为0，表示不包含任何交流信号。

• 情形2

时域上的单脉冲信号，频域上，内含无穷多个谐波分量，且频谱带宽无限，所有谐波分量符合sinc函数的规律。

时域上的sinc信号，在频域上，包含无穷多个谐波分量，但所有的谐波分量的频率被限定在特定的频率带宽内！

（2）数学表达式

（3）实际案例

5. 频移特性

（1）图形表达

时域上：两个信号相乘 x(t) * $\small e^{jw0t}$

频域上：把x（t）的频谱X(ω)搬移到ω0处。

频移特性非常非常的重要！在移动通信和无线通信中，得到了及其广泛的应用。

射频解调和调制，就是利用了傅里叶运算的频移特性！

调制：把基带信号频谱搬移到载波信号的频谱周围。

解调：把调制后信号的频谱，在反向搬移到0频附近，留下基带信号的频谱！

这就是大名鼎鼎的频谱搬移！

（2）数学表达式

时域信号=基带信号：x(t)

基本信号=载波信号：$\small e^{-jw0t}$

频率移动=已调信号：$\small e^{j(w-w0)t}$

复指数运算，很容易得到频谱搬移的结论：

两个复指数函数相乘，实际上就是指数的相加，如下所示：

$\small e^{jwt} * e^{-jw0t} = e^{j(w-w0)t}$

（3）实际案例