【Hello算法】 ＞ 第 3 关 ＞栈与队列

———————————————————————————————————————————————————————————-
————————————————————Hello算法—速通笔记—第三集—start———————–———————————————-

1 栈 / 栈的常见操作、实现、应用

栈（stack）是一种遵循 先入后出 逻辑的线性数据结构。
堆叠元素的顶部称为 “栈顶”，底部称为“栈底”。将把元素添加到栈顶的操作叫作“入栈”，删除栈顶元素的操作叫作“出栈”。

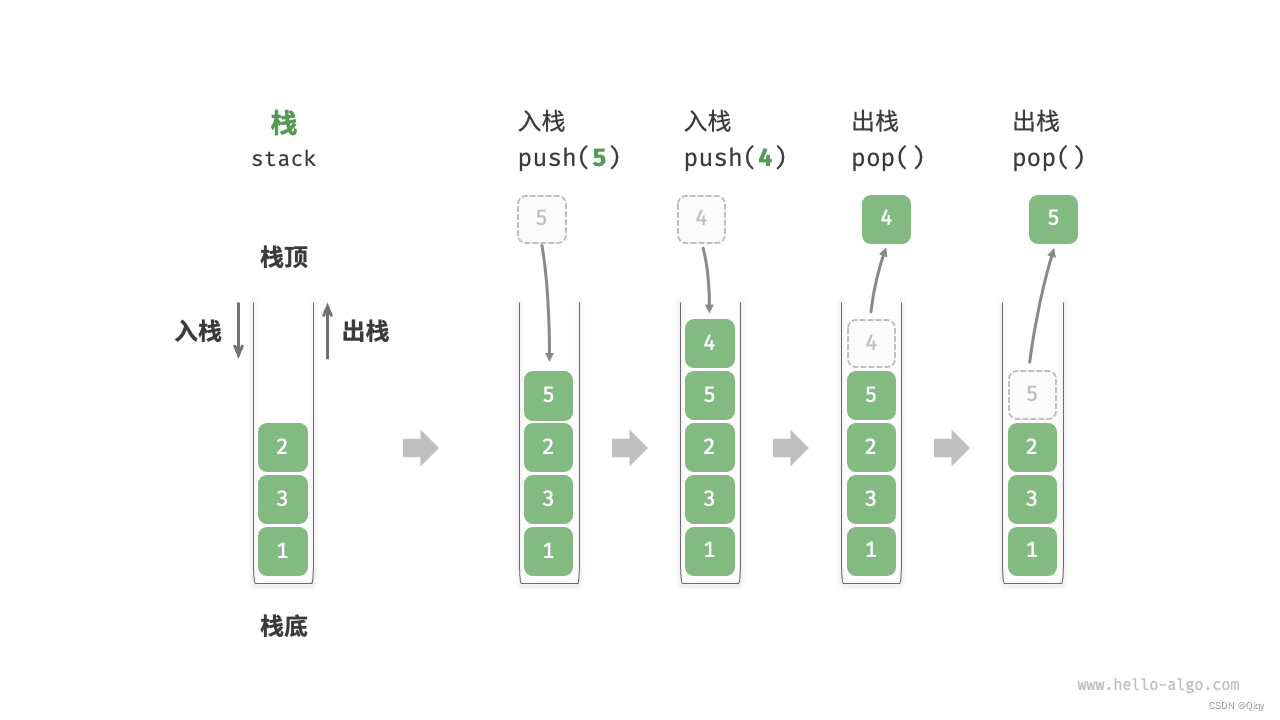
栈的常用操作

/* 初始化栈 */
stack<int> stack;
/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
int top = stack.top();
/* 元素出栈 */
stack.pop(); // 无返回值
/* 获取栈的长度 */
int size = stack.size();
/* 判断是否为空 */
bool empty = stack.empty();
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

栈的实现：
栈可以视为一种受限制的数组或链表。

/* 基于链表实现的栈 */
class LinkedListStack {
  private:
    ListNode *stackTop; // 将头节点作为栈顶
    int stkSize;        // 栈的长度
  public:
    LinkedListStack() {
        stackTop = nullptr;
        stkSize = 0;
    }
    ~LinkedListStack() {
        // 遍历链表删除节点，释放内存
        freeMemoryLinkedList(stackTop);
    }
    /* 获取栈的长度 */
    int size() {     return stkSize;    }
    /* 判断栈是否为空 */
    bool isEmpty() {      return size() == 0;    }
    /* 入栈 */
    void push(int num) {
        ListNode *node = new ListNode(num);
        node->next = stackTop;
        stackTop = node;
        stkSize++;
    }
    /* 出栈 */
    int pop() {
        int num = top();
        ListNode *tmp = stackTop;
        stackTop = stackTop->next;
        // 释放内存
        delete tmp;
        stkSize--;
        return num;
    }
    /* 访问栈顶元素 */
    int top() {
        if (isEmpty())
            throw out_of_range("栈为空");
        return stackTop->val;
    }
    /* 将 List 转化为 Array 并返回 */
    vector<int> toVector() {
        ListNode *node = stackTop;
        vector<int> res(size());
        for (int i = res.size() - 1; i >= 0; i--) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

/* 基于数组实现的栈 */
class ArrayStack {
  private:
    vector<int> stack;
  public:
    /* 获取栈的长度 */
    int size() {     return stack.size();    }
    /* 判断栈是否为空 */
    bool isEmpty() {      return stack.size() == 0;    }
    /* 入栈 */
    void push(int num) {      stack.push_back(num);    }
    /* 出栈 */
    int pop() {
        int num = top();
        stack.pop_back();
        return num;
    }
    /* 访问栈顶元素 */
    int top() {
        if (isEmpty())
            throw out_of_range("栈为空");
        return stack.back();
    }
    /* 返回 Vector */
    vector<int> toVector() {     return stack;    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

对比两种实现：
时间效率：
基于数组实现的栈在触发扩容时效率会降低，但由于扩容是低频操作，因此平均效率更高。
基于链表实现的栈可以提供更加稳定的效率表现。
空间效率：
基于数组实现的栈可能造成一定的空间浪费。
由于链表节点需要额外存储指针，因此链表节点占用的空间相对较大。需要针对具体情况进行分析。
栈的应用：

• 浏览器中的后退与前进、软件中的撤销与反撤销。
• 程序内存管理。

2 队列 /队列的常见操作、实现、应用

队列（queue）是一种遵循 先入先出 规则的线性数据结构。
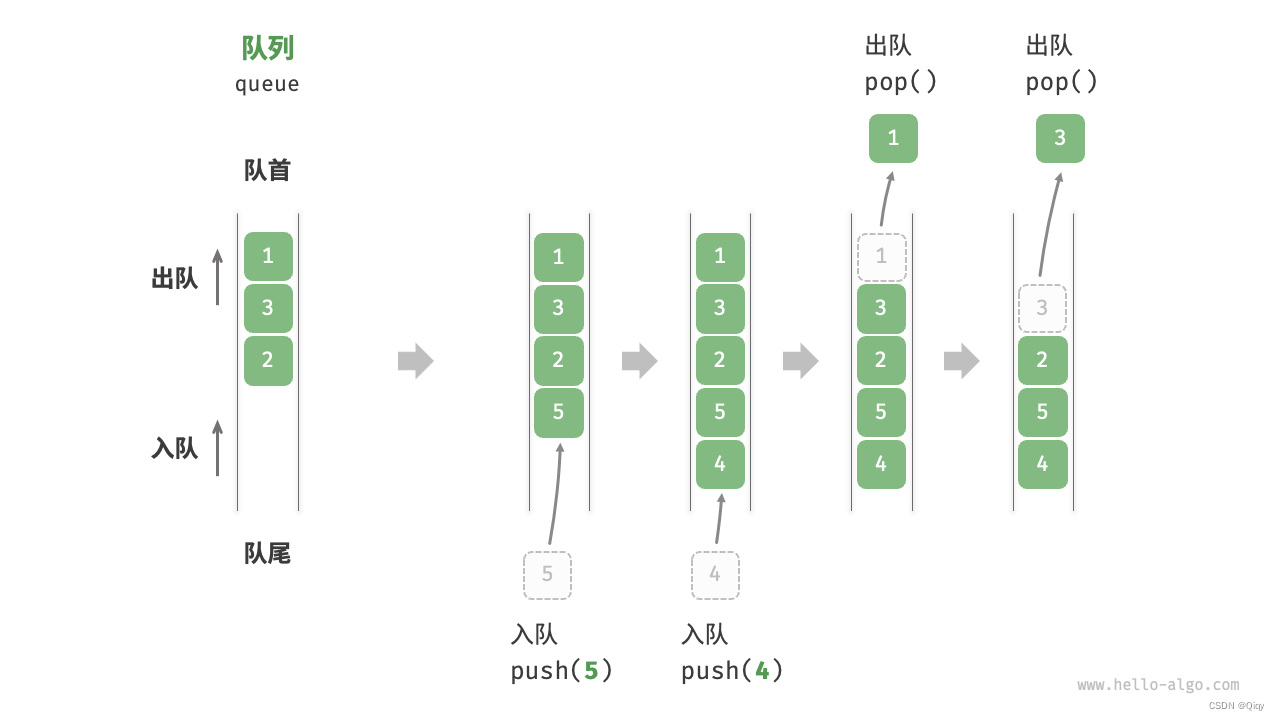队列的常见操作与实现

/* 初始化队列 */
queue<int> queue;
/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);

/* 访问队首元素 */
int front = queue.front();
/* 元素出队 */
queue.pop();
/* 获取队列的长度 */
int size = queue.size();
/* 判断队列是否为空 */
bool empty = queue.empty();
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

/* 基于链表实现的队列 */
class LinkedListQueue {
  private:
    ListNode *front, *rear; // 头节点 front ，尾节点 rear
    int queSize;
  public:
    LinkedListQueue() {
        front = nullptr;
        rear = nullptr;
        queSize = 0;
    }
    ~LinkedListQueue() {
        // 遍历链表删除节点，释放内存
        freeMemoryLinkedList(front);
    }
    /* 获取队列的长度 */
    int size() {     return queSize;    }
    /* 判断队列是否为空 */
    bool isEmpty() {      return queSize == 0;    }
    /* 入队 */
    void push(int num) {
        // 在尾节点后添加 num
        ListNode *node = new ListNode(num);
        // 如果队列为空，则令头、尾节点都指向该节点
        if (front == nullptr) {
            front = node;
            rear = node;
        }
        // 如果队列不为空，则将该节点添加到尾节点后
        else {
            rear->next = node;
            rear = node;
        }
        queSize++;
    }
    /* 出队 */
    int pop() {
        int num = peek();
        // 删除头节点
        ListNode *tmp = front;
        front = front->next;
        // 释放内存
        delete tmp;
        queSize--;
        return num;
    }
    /* 访问队首元素 */
    int peek() {
        if (size() == 0)
            throw out_of_range("队列为空");
        return front->val;
    }
    /* 将链表转化为 Vector 并返回 */
    vector<int> toVector() {
        ListNode *node = front;
        vector<int> res(size());
        for (int i = 0; i < res.size(); i++) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

/* 基于环形数组实现的队列 */
class ArrayQueue {
  private:
    int *nums;       // 用于存储队列元素的数组
    int front;       // 队首指针，指向队首元素
    int queSize;     // 队列长度
    int queCapacity; // 队列容量
  public:
    ArrayQueue(int capacity) {
        // 初始化数组
        nums = new int[capacity];
        queCapacity = capacity;
        front = queSize = 0;
    }
    ~ArrayQueue() {     delete[] nums;    }
    /* 获取队列的容量 */
    int capacity() {      return queCapacity;    }
    /* 获取队列的长度 */
    int size() {        return queSize;    }
    /* 判断队列是否为空 */
    bool isEmpty() {      return size() == 0;    }
    /* 入队 */
    void push(int num) {
        if (queSize == queCapacity) {
            cout << "队列已满" << endl;
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        // 通过取余操作实现 rear 越过数组尾部后回到头部
        int rear = (front + queSize) % queCapacity;
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }
    /* 出队 */
    int pop() {
        int num = peek();
        // 队首指针向后移动一位，若越过尾部，则返回到数组头部
        front = (front + 1) % queCapacity;
        queSize--;
        return num;
    }
    /* 访问队首元素 */
    int peek() {
        if (isEmpty())
            throw out_of_range("队列为空");
        return nums[front];
    }
    /* 将数组转化为 Vector 并返回 */
    vector<int> toVector() {
        // 仅转换有效长度范围内的列表元素
        vector<int> arr(queSize);
        for (int i = 0, j = front; i < queSize; i++, j++) {
            arr[i] = nums[j % queCapacity];
        }
        return arr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

应用·：

• 淘宝订单
• 各类待办事项

3 双向队列

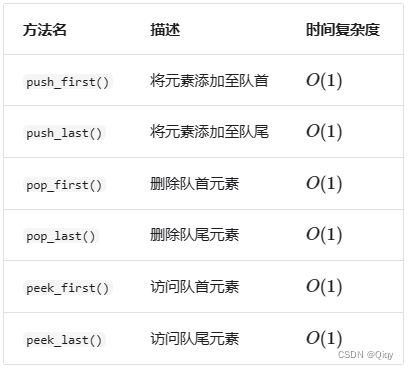
双向队列（double-ended queue）提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作。
常用操作

/* 初始化双向队列 */
deque<int> deque;
/* 元素入队 */
deque.push_back(2);   // 添加至队尾
deque.push_back(5);
deque.push_back(4);
deque.push_front(3);  // 添加至队首
deque.push_front(1);
/* 访问元素 */
int front = deque.front(); // 队首元素
int back = deque.back();   // 队尾元素
/* 元素出队 */
deque.pop_front();  // 队首元素出队
deque.pop_back();   // 队尾元素出队
/* 获取双向队列的长度 */
int size = deque.size();
/* 判断双向队列是否为空 */
bool empty = deque.empty();
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

实现

/* 双向链表节点 */
struct DoublyListNode {
    int val;              // 节点值
    DoublyListNode *next; // 后继节点指针
    DoublyListNode *prev; // 前驱节点指针
    DoublyListNode(int val) : val(val), prev(nullptr), next(nullptr) {
    }
};
/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
  private:
    DoublyListNode *front, *rear; // 头节点 front ，尾节点 rear
    int queSize = 0;              // 双向队列的长度
  public:
    /* 构造方法 */
    LinkedListDeque() : front(nullptr), rear(nullptr) {
    }
    /* 析构方法 */
    ~LinkedListDeque() {
        // 遍历链表删除节点，释放内存
        DoublyListNode *pre, *cur = front;
        while (cur != nullptr) {
            pre = cur;
            cur = cur->next;
            delete pre;
        }
    }
    /* 获取双向队列的长度 */
    int size() {      return queSize;    }
    /* 判断双向队列是否为空 */
    bool isEmpty() {       return size() == 0;    }
    /* 入队操作 */
    void push(int num, bool isFront) {
        DoublyListNode *node = new DoublyListNode(num);
        // 若链表为空，则令 front 和 rear 都指向 node
        if (isEmpty())
            front = rear = node;
        // 队首入队操作
        else if (isFront) {
            // 将 node 添加至链表头部
            front->prev = node;
            node->next = front;
            front = node; // 更新头节点
        // 队尾入队操作
        } else {
            // 将 node 添加至链表尾部
            rear->next = node;
            node->prev = rear;
            rear = node; // 更新尾节点
        }
        queSize++; // 更新队列长度
    }
    /* 队首入队 */
    void pushFirst(int num) {       push(num, true);    }
    /* 队尾入队 */
    void pushLast(int num) {        push(num, false);    }
    /* 出队操作 */
    int pop(bool isFront) {
        if (isEmpty())
            throw out_of_range("队列为空");
        int val;
        // 队首出队操作
        if (isFront) {
            val = front->val; // 暂存头节点值
            // 删除头节点
            DoublyListNode *fNext = front->next;
            if (fNext != nullptr) {
                fNext->prev = nullptr;
                front->next = nullptr;
            }
            delete front;
            front = fNext; // 更新头节点
        // 队尾出队操作
        } else {
            val = rear->val; // 暂存尾节点值
            // 删除尾节点
            DoublyListNode *rPrev = rear->prev;
            if (rPrev != nullptr) {
                rPrev->next = nullptr;
                rear->prev = nullptr;
            }
            delete rear;
            rear = rPrev; // 更新尾节点
        }
        queSize--; // 更新队列长度
        return val;
    }
    /* 队首出队 */
    int popFirst() {       return pop(true);    }
    /* 队尾出队 */
    int popLast() {    return pop(false);    }
    /* 访问队首元素 */
    int peekFirst() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return front->val;
    }
    /* 访问队尾元素 */
    int peekLast() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return rear->val;
    }
    /* 返回数组用于打印 */
    vector<int> toVector() {
        DoublyListNode *node = front;
        vector<int> res(size());
        for (int i = 0; i < res.size(); i++) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114

/* 基于环形数组实现的双向队列 */
class ArrayDeque {
  private:
    vector<int> nums; // 用于存储双向队列元素的数组
    int front;        // 队首指针，指向队首元素
    int queSize;      // 双向队列长度
  public:
    /* 构造方法 */
    ArrayDeque(int capacity) {
        nums.resize(capacity);
        front = queSize = 0;
    }
    /* 获取双向队列的容量 */
    int capacity() {
        return nums.size();
    }
    /* 获取双向队列的长度 */
    int size() {
        return queSize;
    }
    /* 判断双向队列是否为空 */
    bool isEmpty() {
        return queSize == 0;
    }
    /* 计算环形数组索引 */
    int index(int i) {
        // 通过取余操作实现数组首尾相连
        // 当 i 越过数组尾部后，回到头部
        // 当 i 越过数组头部后，回到尾部
        return (i + capacity()) % capacity();
    }
    /* 队首入队 */
    void pushFirst(int num) {
        if (queSize == capacity()) {
            cout << "双向队列已满" << endl;
            return;
        }
        // 队首指针向左移动一位
        // 通过取余操作实现 front 越过数组头部后回到尾部
        front = index(front - 1);
        // 将 num 添加至队首
        nums[front] = num;
        queSize++;
    }
    /* 队尾入队 */
    void pushLast(int num) {
        if (queSize == capacity()) {
            cout << "双向队列已满" << endl;
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        int rear = index(front + queSize);
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }
    /* 队首出队 */
    int popFirst() {
        int num = peekFirst();
        // 队首指针向后移动一位
        front = index(front + 1);
        queSize--;
        return num;
    }
    /* 队尾出队 */
    int popLast() {
        int num = peekLast();
        queSize--;
        return num;
    }
    /* 访问队首元素 */
    int peekFirst() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return nums[front];
    }
    /* 访问队尾元素 */
    int peekLast() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        // 计算尾元素索引
        int last = index(front + queSize - 1);
        return nums[last];
    }
    /* 返回数组用于打印 */
    vector<int> toVector() {
        // 仅转换有效长度范围内的列表元素
        vector<int> res(queSize);
        for (int i = 0, j = front; i < queSize; i++, j++) {
            res[i] = nums[index(j)];
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94

应用

• 双向队列兼具栈与队列的逻辑，因此它可以实现这两者的所有应用场景，同时提供更高的自由度。

4 Tips

1. 浏览器的前进后退功能本质上是“栈”的体现。
2. 在出栈后，如果后续仍需要使用弹出节点则不需要释放内存，反之则c/c++需要手动释放内存。
3. 双向队列表现的是栈+队列的逻辑，可实现栈与队列的所有应用，且更灵活。
4. 撤销（undo）与反撤销（redo）的实现：
   使用两个栈，栈 A 用于撤销，栈 B 用于反撤销。
   每当用户执行一个操作，将这个操作压入栈 A ，并清空栈 B 。
   当用户执行“撤销”时，从栈 A 中弹出最近的操作，并将其压入栈 B 。
   当用户执行“反撤销”时，从栈 B 中弹出最近的操作，并将其压入栈 A 。

————————————————————————————————————————————————————————————
—————————————————————Hello算法—速通笔记—第三集—end—————————————————————–—-