网络安全与密码学

一、密码学概述

一、

密码学是一门研究信息安全保密的学科，主要涉及对信息进行加密、解密以及相关的安全技术和理论。 它通过使用各种加密算法和技术，将明文信息转换为密文，以确保信息在传输和存储过程中的保密性、完整性和真实性。密码学在通信、电子商务、金融、军事等领域都有着广泛的应用。 密码学包括对称加密、非对称加密、哈希函数、数字签名等重要内容。同时，密码学也在不断发展和创新，以应对不断变化的安全挑战。

大家要注意的是我们平时用来认证身份的密码（passwd）翻译成口令更准确。而我们这里的密码是指把正常的、可识别的信息转换成一种不可识别的信息的技术（或者产品服务）。除此以外密码技术还用来做安全认证，比如用来确定信息是否被篡改、是否来自可靠信息源以及确认行为是否真实等。

密码学的发展历史可以追溯到古代，人类使用密码的历史几乎与使用文字的时间一样长。

密码学发展的主要阶段：

1. 古典密码学阶段：从密码的产生到发展成为近代密码之间的这段时期，主要特点是手工加解密，也被称为手工密码时代。

2. 近代密码学阶段：从一战、二战到 1976 年，该阶段的主要特点是采用机械或机电密码机进行加密和解密，也被称为机电密码时代。

3. 现代密码学阶段：1976 年以后，对称密钥密码算法得到进一步发展，产生了密码学的新方向—公钥密码学。 随着科技的不断发展，密码学也在不断演进和创新，以应对日益复杂的信息安全挑战。在现代，密码学广泛应用于通信、电子商务、金融、军事等领域，对保护信息的安全和隐私起着至关重要的作用。

我们使用最为粗略的划分方法。直接划分成古典密码和现代密码。

古典密码和现代密码的分界线是什么呢？

一般来说，我们是根据加密方式来区分古典密码学和现代密码学。

一般来说，古典密码学是基于字符的，使用手工或者机械的方式加密。

而现代密码学是基于二进制位的，也就是引入了计算机的使用。

古典密码学和近代密码学主要有以下一些区别：

1. 加密手段：古典密码学主要依靠简单的替换、置换等方法；近代密码学则采用更复杂的机械或机电装置来加密。

2. 安全性：近代密码学的安全性相对更高，加密算法更为复杂。

3. 应用范围：近代密码学的应用范围更广，不仅用于军事等领域，也逐渐在商业等方面得到应用。

以下是一些著名的古典密码学和近代密码学案例：

古典密码学：

1. 凯撒密码：通过将字母表中的字母移动一定的位置来加密。

近代密码学：

1. 恩尼格玛密码机：二战时期德国使用的加密机器，曾给盟军造成很大困扰。

古典密码学： 优点：简单易懂，在某些特定情况下仍有一定作用。 缺点：加密强度较低，容易被破解。

近代密码学： 优点：加密机制更复杂，安全性较高。 缺点：操作相对复杂，需要一定的技术和设备支持。

除了古典密码学和近代密码学中的方法外，现代密码学还包括以下方法：

1. 散列函数：将任意长度的输入消息转换为固定长度的哈希值。常见的散列函数包括 MD5、SHA-1、SHA-256 和 SHA-512 等。

2. 对称加密：使用相同的密钥进行加密和解密。常见的对称加密算法包括 DES、3DES、AES 等。

3. 非对称加密：使用公钥和私钥进行加密和解密。公钥可以公开，私钥则只有拥有者知道。常见的非对称加密算法包括 RSA、DSA 等。

4. 数字签名：用于验证消息的来源和完整性。签名者使用私钥对消息进行签名，接收者使用对应的公钥验证签名的有效性。

5. 身份验证协议：如OAuth、SSH 等，用于在网络环境中进行身份验证和授权。

6. 区块链技术：如比特币中的加密算法，用于保证交易的安全性和不可篡改性。 这些方法在不同的应用场景中都有广泛的应用，并且随着技术的不断发展，密码学也在不断地演进和创新。

密码系统组成结构
密码系统指的是一个用于加/解密， 能够解决网络安全中的机密性、 完整性、 可用性、 可控性和真实性等问题中的一个或几个的系统。

符号表示与含义
1、明文 P/M（Plaintext）：需要加密的原始信息

2、密文 C（Ciphertext）：明文经过变换或伪装， 形成密文

3、密码算法：加密变换与解密变换的具体规则

4、加密 E（Encryption）：对明文实施的一系列变换过程

5、解密 D（Decrption）：对密文施加的一系列的逆变换还原明文的过程

6、密钥——加密参数

重点解释一下什么叫做密钥：

早期的加密方式，就是最关键的信息。只要加密方式被破解，就没有秘密可言了。这个时候不得不设计新的加密方法。

怎么解决这个问题呢？我们可以在加密方法里面加入控制密码处理过程的关键信息，这个东西就叫密钥。当一个密钥泄露的时候，我们只需要更换密钥就可以了。这样大大地提升了安全性，也减少了操作成本。

只要我们设计的算法足够好，那么密钥就是很难猜出来的。密钥是加密的关键，所以必须保护好。

在不知道密钥的情况下，很难从输出结果（密文）推算出输入内容（明文），这个是怎么做到的呢？它依赖的是数学上的单向陷门函数。

密码系统组成结构
密码系统指的是一个用于加/解密， 能够解决网络安全中的机密性、 完整性、 可用性、 可控性和真实性等问题中的一个或几个的系统。

符号表示与含义
1、明文 P/M（Plaintext）：需要加密的原始信息

2、密文 C（Ciphertext）：明文经过变换或伪装， 形成密文

3、密码算法：加密变换与解密变换的具体规则

4、加密 E（Encryption）：对明文实施的一系列变换过程

5、解密 D（Decrption）：对密文施加的一系列的逆变换还原明文的过程

6、密钥——加密参数

重点解释一下什么叫做密钥：

早期的加密方式，就是最关键的信息。只要加密方式被破解，就没有秘密可言了。这个时候不得不设计新的加密方法。

怎么解决这个问题呢？我们可以在加密方法里面加入控制密码处理过程的关键信息，这个东西就叫密钥。当一个密钥泄露的时候，我们只需要更换密钥就可以了。这样大大地提升了安全性，也减少了操作成本。

只要我们设计的算法足够好，那么密钥就是很难猜出来的。密钥是加密的关键，所以必须保护好。

在不知道密钥的情况下，很难从输出结果（密文）推算出输入内容（明文），这个是怎么做到的呢？它依赖的是数学上的单向陷门函数。

密钥可以分为：

加密密钥 Ke/Pk(public key)

解密密钥 Kd/Sk (secret key)

对于对称加密，秘钥是同一把。

对于非对称加密，（Sk，Pk）是一对。

密码系统安全性
柯克霍夫（Kerckhoff）原则
密码的安全性取决于密钥，而不是密码算法，即密码算法要公开。

柯克霍夫原则是现代密码学算法设计基本原则之一，最早由荷兰密码学家Auguste Kerckhoffs在1883的论文La 《Cryptographie Militaire》（《军用密码学》）中提出。

评估方法
评估密码系统安全性主要有三种方法：

无条件安全
（1）无条件安全：假定攻击者拥有无限的资源（时间、计算能力)，仍然无法破译加密算法。无条件安全属于极限状态安全。

计算安全
（2）计算安全：破解加密算法所需要的资源是现有条件不具备的，则表明强力破解证明是安全的。计算安全属于强力破解安全。

举个例子，设一个密码算法E的密钥K是128比特，加密过程为C=E(K,P)，已知一个明文-密文对(P,C),但是不知道K。

求K，这个问题不是理论安全的，因为我们可以穷举2^128种可能；但是这个问题是计算安全的，因为即使一秒钟可以穷举1000亿个K,要穷举2^128个K要花费超过100 000 000 000 000 000 年的时间，在实践中是安全的。

可证明安全
（3）可证明安全：密码系统的安全性归结为经过深入研究的数学难题（例如大整数素因子分解、计算离散对数等)。可证明安全属于理论保证安全。

密码系统的安全强度主要与以下因素有关：

1. 加密算法的复杂性：算法越复杂，破解难度越大。 2. 密钥长度：较长的密钥能提供更高的安全性。 3. 密钥管理：妥善管理密钥，防止泄露或被窃取。 4. 抗攻击能力：对各种攻击手段的抵抗能力。 5. 随机数生成的质量：确保生成高质量的随机数用于加密。 6. 系统的更新与维护：及时修补漏洞，适应新的安全挑战。

安全标准
对于实际应用中的密码系统而言，由于至少存在一种破译方法，即强力攻击法，因此都不能满足无条件安全性，只提供计算安全性。密码系统要达到实际安全性，就要满足以下准则:
(1）破译该密码系统的实际计算量（包括计算时间或费用)十分巨大，以致于在实际上是无法实现的。
(2）破译该密码系统所需要的计算时间超过被加密信息有用的生命周期。例如，战争中发起战斗攻击的作战命令只需要在战斗打响前需要保密;重要新闻消息在公开报道前需要保密的时间往往也只有几个小时。

举例：2000年偷了100台BB机，被判了20年。出来以后发现已经没人用BB机了。
(3)破译该密码系统的费用超过被加密信息本身的价值。
如果一个密码系统能够满足以上准则之一，就可以认为是满足实际安全性的。

举例：捡了很多矿泉水瓶子，为了多卖2块钱，开车到20公里外的废品站去卖。

以下是一些常见的攻击密码的方法：

1. 暴力破解：通过尝试所有可能的组合来破解密码。

2. 字典攻击：利用预先准备好的字典来猜测密码。

3. 中间人攻击：攻击者在通信双方之间进行拦截和篡改。

4. 侧信道攻击：利用密码系统执行过程中泄露的信息进行攻击。

5. 密码分析：通过分析密码算法的弱点来破解密码。

抗攻击能力是指密码系统抵御各种恶意攻击的能力。 这些攻击包括但不限于：暴力破解、字典攻击、差分分析、线性分析、旁路攻击等。一个具有较强抗攻击能力的密码系统能够在面对这些攻击时，保持信息的保密性、完整性和可用性，确保系统的安全可靠。

攻击方法
攻击密码方法：

（在加密算法公开的前提下）

1、穷举攻击：对截获到的密文尝试遍历所有可能的密钥，直到获得正确的明文；或使用固定的密钥对所有可能的明文加密一直到得到与截获到的密文一致为止。

所有的密码系统都可以用穷举法来攻击。对抗穷举攻击最有效的对策是设法将密钥空间和明文空间、密文空间设计得足够大

2、统计分析：利用已经获取的明文和密文已知统计规律进行破译的方法。

例如,许多古典密码都可以通过分析字母和字母组合的频率分布以及其他统计参数来破译。

对抗统计分析攻击法最有效的对策是:设法使明文的统计特性不带入密文,扰乱密文的语言统计规律,即把密文和明文的统计特性扩散到整个密文,这样使得密文不呈现任何明文的统计特性,反而呈现出极大的随机性,从而使统计分析攻击法无法达到目的。

3、数学分析攻击：密码分析者针对加解密算法的数学基础和密码学特性，通过数学求解的方法来破译密码。

数学攻击是对基于数学难题的各种密码算法的重大威胁。数学法也称为确定性攻击法或系统攻击法。

对抗数学分析攻击法的对策是设计和选用具有坚实数学基础和足够复杂的加密函数。

攻击类型
唯密文攻击（Ciphertext Only Attack，COA）
定义：唯密文攻击(COA)是指仅仅知道密文的情况下进行分析，求解明文或密钥的密码分析方法。

假定密码分析者拥有密码算法及明文统计特性，并截获了一个或者多个用同一密钥加密的密文，通过对这些密文进行分析求出明文或密钥。COA已知条件最少，经不起唯密文攻击的密码是被认为不安全的。

简单理解：只知道密文，推出明文或密钥，一般用穷举攻击。

已知明文攻击（Known Plaintext Attack，KPA）
定义：已知明文攻击(KPA)是指攻击者掌握了部分的明文M和对应的密文C，从而求解或破解出对应的密钥和加密算法。

简单理解：知道部分的明文和密文对，推出密钥和加密算法。

选择明文攻击（Chosen Plaintext Attack，CPA）
定义：选择明文攻击(CPA)是指攻击者除了知道加密算法外，还可以选定明文消息，从而得到加密后的密文，即知道选择的明文和加密的密文，但是不能直接攻破密钥。

简单理解：知道明文就知道密文，目标为推出密钥。

选择密文攻击（Chosen Ciphertext Attack，CCA）
若一个密码系统能抵抗选择密文攻击，那必然能够抵抗COA和KPA攻击。密码分析者的目标是推出密钥，CCA主要应用于分析公钥密钥体制。

简单理解：知道密文就知道明文，目标为推出密钥。

密码学分支
密码学包括密码编码学和密码分析学两个分支。

密码编码学是研究密码变化的客观规律，设计各种编码体系对信息进行变换，以保护信息在信道的传递过程中不被敌手窃取、解读和利用；

而密码分析学则与密码编码学相反，密码分析学对密码进行分析，在未知密钥的情况下，从密文推出明文或密钥，这是对加密信息进行解密的过程，也就是俗语所说的破解密码，密码分析学主要研究的就是如何分析和破译密码。

在整个密码学的发展中，这看似对立的两门学科却是相辅相成、互相促进，推动了密码学一代又一代的发展。

加密方式为什么会不断升级呢？就是因为每一次我们都觉得这种加密方式非常安全了，但是却又被破解了。所以不得不研究新的加密方式。

我们现在的加密技术是不是无懈可击的呢？现在看来是这样，但是说不定以后就会被破解。

这跟我们的安全攻防也是一样的，攻击技术的不断升级，就会促使防御技术的不断升级。

编码和加密有以下区别：

编码：

1. 主要目的是将信息从一种形式转换为另一种形式，以便于存储、传输或处理。 2. 通常是可逆的，即可以通过解码将编码后的信息还原为原始信息。 3. 不提供保密性，信息在编码后仍然是可见的。

加密： 1. 旨在对信息进行保护，使其在传输或存储过程中不被未经授权的人获取。 2. 是不可逆的（在大多数情况下），只有拥有正确密钥的人才能将密文解密为明文。 3. 提供保密性，加密后的信息对于未授权的人来说是难以理解的。

密码学与网络安全有着密切的关系。 密码学是网络安全的重要基石，它为网络安全提供了关键的技术手段，如加密通信、身份认证、数字签名等，能够有效保护网络中的信息不被窃取、篡改或伪造，确保网络系统的机密性、完整性和可用性。 同时，网络安全的发展也推动着密码学的不断进步和创新，以应对日益复杂的网络安全挑战。

密码学与网络安全

网络安全的基本属性包括机密性、完整性、可用性、可认证性和不可否认性。

1. 机密性：确保信息不被未授权的人获取。例如，在密码学中，通过加密算法将明文转换为密文，只有拥有正确密钥的人才能解密获取信息。

2. 完整性：保证信息在传输和存储过程中不被篡改。密码学中的哈希函数可以用于验证信息的完整性。

3. 可用性：保证授权用户能够及时、可靠地访问信息。这与密码学中的身份认证等技术相关，确保合法用户能够正常使用系统。

4. 可认证性：确认通信或操作的双方是真实的。密码学中的数字证书、数字签名等技术可实现身份的认证。

5. 不可否认性：防止发送方或接收方否认曾经进行的操作。密码学中的数字签名可以提供不可否认性的证据。

密码学解密网站汇总 - 菜鸟-传奇 - 博客园 (cnblogs.com)

二、古典密码

这需要大家有一些基本的数学知识，初中的数学就够用，比如什么叫取模，什么叫公约数，什么叫质数，什么叫阶乘，还有一点排列组合的知识等等。

主要内容包括：

替换密码

单表替换密码：

字符或数字：

凯撒密码
简单替换密码
仿射密码
普莱费尔密码
培根密码

图表：

猪圈密码
摩斯密码

多表替换密码：

 维吉尼亚密码 

移位密码

滚筒密码
栅栏密码

机械密码

恩格玛密码机

古典密码的两个主要体制是替换密码（Simple Substitution Cipher）（或者叫代换）和移位密码（Permutation Cipher 或 Transposition Cipher）（或者叫置换）。

后面说到的机械密码也是一种复杂的多表替换，不过因为它的加密方式已经从手工编程了机械，所以我们把它单独拿出来。

按照替换表的数量
替换密码采用一个代换表，将一段明文变换成一段密文，这个代换表就是密钥。如果替换表只有一个，则替换过程被称为单表替换。如果替换表多于一个，则替换过程被称为多表替换。

移位密码是一种特殊的替换密码，替换密码替换过程不改变明文内容，只改变它们的位置。

按照替换的内容
分为字符、数字，和图表型。

三、对称加密算法

序列密码（流密码）：RC4

分组密码（块加密）：DES 3DES AES TDEA

现代密码学具有三大里程碑事件，奠定了现代密码学的基础。

密码学发展史上的第一座里程碑性事件是划时代的内部报告《A Mathematical Theory of Cryptography（密码的一个数学理论）》的发表。1945年9月1日，Claude Elwood Shannon（克劳德•艾尔伍德•香农）完成了划时代的内部报告《A Mathematical Theory of Cryptography（密码的一个数学理论）》

1949年10月，该报告以《Communication Theory of Secrecy Systems（保密系统的通信理论）》为题在 Bell System Technical Journal（贝尔系统技术期刊）上正式发表。这篇论文首次将密码学和信息论联系到一起，为对称密码技术提供了数学基础。这也标志着近现代密码学的正式建立。

密码学发展史上的第二个里程碑性事件是DES的出现。DES全称为Data Encryption Standard，即美国数据加密标准，是一种使用密钥加密的分组密码算法，1972年左右出现，1977年被美国联邦政府的国家标准局确定为联邦资料处理标准（FIPS），并授权在非密级政府通信中使用，随后该算法在国际上广泛流传开来。

密码学发展史上的第三个里程碑性事件就是我们区块链中广泛应用的公钥密码，也就是非对称密码算法的出现。1976年11月，Whitfield Diffie 和 Martin E.Hellman 在 IEEE Transactions on Information Theory 上发表了论文《New Directions in Cryptography（密码学的新方向）》，探讨了无需传输密钥的保密通信和签名认证体系问题，正式开创了现代公钥密码学体系的研究。

现代密码里面，又可以分成两大类，对称密码和非对称密码。

对称密码和非对称密码
它们两个的区别是加解密是否使用相同的密钥。

我们县看对产加密，也叫共享密钥加密。

左边是消息发送方，右边是消息接收方

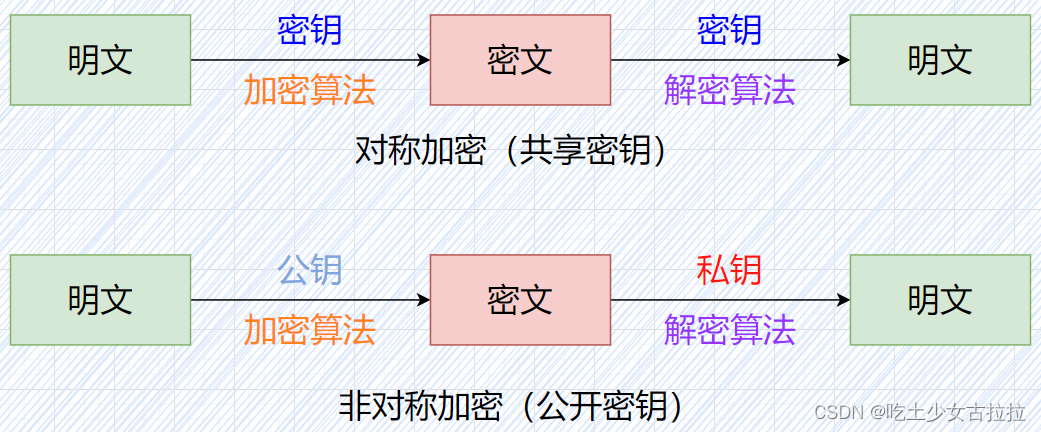
对称加密
对称加密又称单密钥加密，整个加密过程中只使用一个密钥。这个就是对称的名字的来源。常用的对称加密算法有 DES、3DES、AES、TDEA、Blowfish、RC2、RC4 和 RC5 等。

非对称加密
非对称加密又称为公钥密码，该技术是针对私钥密码体制（对称加密算法）的缺陷被提出来的，非对称加密会产生两把密钥，分别为公钥（Public Key）和私钥（Private Key），其中一把密钥用于加密，另一把密钥用于解密。常用的非对称加密算发有 RSA、Elgamal、背包算法、Rabin、D-H、ECC（椭圆曲线加密算法）等。非对称加密的特征是算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂，而使得加密解密速度没有对称加密解密的速度快。对称密码体制中只有一种密钥，并且是非公开的，如果要解密就得让对方知道密钥。所以保证其安全性就是保证密钥的安全，而非对称密钥体制有两种密钥，其中一个是公开的，这样就可以不需要像对称密码那样传输对方的密钥了。这样安全性就高了很多。

混合加密-对称加密和非对称加密的实际应用场景
所谓混合加密就是使用在实际的应用中把对称加密和非对称加密结合起来使用。我们都知道非对称加密算法比对称加密算法慢数千倍，但在保护通信安全方面，非对称加密算法却具有对称密码难以企及的优势。所以在实际的应用中，都是对称加密与非对称加密混合使用。取其优势，去其糟粕，达到完美使用的一个目的。

那我们我们学习先发明的，比较简单的对称密码。

对称密码按照加密的方式，又可以分为两类，一种叫做流密码，一种叫做分组密码。

对称密码分类
对称加密算法一般分为流密码（序列加密）和分组密码（块加密）。

流密码的加密单位比较小，比如以1个位（bit）或者一个字节（8bit）为单位进行加密。

分组密码的加密单位更大，不是一个字节或者一个位，比如DES的明文分组长度是64位，AES的明文分组长度是128位。

流密码概念
在流密码里面，会产生一个密钥流（密钥序列），和明文一一对应进行加密，得到密文序列，然后组合到一起就是加密后的密文。

实践中数据通常是对每一个位（bit）并用异或（xor）操作加密。异或操作有一个特点，就是异或两次以后会得到原来的数据。

这个密钥流也叫做伪随机密钥流，它是由种子密钥得到的，种子密钥是我们自己输入的一个密钥。这个通过种子密钥生成密钥流的过程叫做：PRG，pseudo-random generator。

一般来说，种子密钥的长度比较短，而密钥流的长度需要跟明文的长度一样。

流密码特点
加密速度快。主要使用异或运算。

动态加密，不需要提前加载大量内容到寄存器中，不用很大的缓冲区。

RC4算法
RC4，全称：Rivest Cipher 4（Ron Rivest，1987）

RC4是一种典型的流加密算法，密钥长度可变。

RC4已经成为一些常用的协议和标准的一部分，如1997年的WEP和2003/2004年无线卡的WPA; 和1995年的SSL，以及后来1999年的TLS。让它如此广泛分布和使用的主要因素是它不可思议的简单和速度，不管是软件还是硬件，实现起来都十分容易。

分组密码
学习了流密码和作为代表的RC4算法之后，我们再来看分组密码。

和流密码不一样，分组密码的加密单位更大，不是一个字节或者一个位，比如DES的明文分组长度是64位，AES的明文分组长度是128位。一个分组或者叫做一个块的内容是一起处理的。同样的，得到了分块的密文以后，组合在一起，就是完整的密文。

分组密码的设计原则
香农《保密系统的通信理论》提出的分组密码的设计原则：

混淆：打乱密文、明文、秘钥之间的依赖关系,使得敌手获得密文和明文的统计规律，也无法求出秘钥。——使用替换实现
扩散：让密文中的每一位受明文中的尽可能多位的影响。——使用移位实

为什么要分组呢？让每一个子块计算更简单。

DES加密算法
DES算法是属于对称密码的分组加密算法。秘钥长64位，56位参与运算，其余8位为效验位（ 8 , 16 , 32 , 40 , 48 , 56 , 64 ）当n个64位明文数据块都经过DES加密处理后，所得到的n个64位密文数据块串在一起就

DES 算法是分组加密算法的典型代表，同时也是应用最为广泛的对称加密算法

3DES
3DES，即Triple-DES，简单地说就是3次DES加解密的组合。3DES算法是国内银行业广泛使用的一种对称加密算法。在金融行业里，其流行程度可能还略高于经典的AES。甚至有些金融科技机构推行的加密标准中，3DES位列其中而AES却没有一席之地。加密：cipthertext = E(k3, D(k2, E(k1, plaintext)))解密：plaintext = D(k1, E(k2, D(k3, ciphertext)))特点：如果三个密钥都一样，那刚好和DES一样。3DES只是一个过渡方案。

AES（Advanced Encryption Standard，高级加密标准）是一种广泛应用的对称加密算法。AES 的主要参数包括： 1. 分组长度：128 位。 2. 密钥长度：可以是 128 位、192 位或 256 位。 3. 轮数：不同密钥长度对应的轮数不同。 它具有较高的安全性和效率，采用分组密码模式，支持 128 位、192 位和 256 位三种不同的密钥长度。AES 在现代网络安全中起着重要作用，被用于保护各种敏感信息。

对称加密的主要有优点就是算法公开、计算量小、加密速度快、加密效率高；但是它也存在强大的缺点，缺点就是密钥协商过程中，一旦密钥泄露，别人可以获取到密钥，这样也能对密文进行解密。另外，每对用户每次使用对称加密算法时，都需要使用其他人不知道的独一密钥，这会使得收、发双方所拥有的钥匙数量巨大，密钥管理成为双方的负担

四、非对称加密算法

 

我们有没有不担心加密密钥泄露，可以直接把加密密钥公开的方法呢？

这个就是我们说的公开密钥加密，也叫做非对称加密算法。

使用算法可以生成两把密钥 A 和 B
使用 A 加密的信息，使用 B 可以解开
使用 B 加密的信息，使用 A 可以解开

非对称加密的大致流程
假设A是消息发送方，B是消息接收方：
1、A生成一个密钥对，一个叫做公钥，一个叫做私钥。公私钥对是根据一定的计算规则生成的，不能像对称加密算法一样自己定义。

其中，公钥用来加密消息，可以公开给任何想要发送消息给A的人。

私钥用来解密消息，只有A用户保密持有。

2、B用户获得A用户的公钥以后，用公钥对消息加密。

3、A用户得到B用户发送的加密消息，用私钥解密消息。如果没有私钥或者私钥不匹配，就无法解密消息。

因为非对称加密的特性，现在我们就可以把密钥直接公布出去了。只要私钥没有泄露，通信就是安全的。

日常使用中，我们把一把作为公钥，公开发布。一把作为私钥，自己保留。这样，任何人都可以使用我们的公钥加密信息发给我们，我们则可以使用自己的私钥解开。

只要把私钥保存好，这个通信系统就非常安全。

非对称加密加密算法的数学基础
加密和解密使用的密钥不一样，这个就叫做非对称。

那怎么实现这种非对称性呢？主要思想就是利用数学上的一些问题的“非对称性”。

也就是说，从一个方向计算非常容易，而从另一个方向计算则很困难，这个保证了算法可以实现，也保证了算法的安全性。

在DH算法的基础上实现的非对称加密算法，主要基于数学问题求解，可以分两类：

1、基于因子分解难题：代表算法为RSA算法
2、基于离散对数难题：代表算法ElGamal算法、DSA（Digital Signature Algorithm， 数字签名算法）
3、椭圆曲线类：ECC（Elliptical Curve Cryptography, 椭圆曲线加密算法）。

对称加密算法的优点是计算开销小、加密速度快，适用于海量数据的加密，是目前用于信息加密的主要算法。非对称加密算法可以适应网络的开放性要求，且密钥管理问题也较为简单，可方便地实现数字签名和验证。缺点是算法复杂、加密数据的速率较低。所以不存在哪类加密算法比哪类加密算法更加高级，哪类算法会被淘汰的问题。对称加密和非对称加密是经常一起使用的，用来解决不同的问题，这种加密方式叫做混合加密。而且，有了混合加密还不够，内容被篡改的问题，还要进一步结合哈希算法来解决。身份信任的问题，还要通过PKI（公钥基础设施），这样才能构成一个完整的密码系统。

哈希算法分类
目前常见的典型哈希算法包括CRC、MD5、SHA1和SHA2等，这些算法其实背后都有一个家族，同一家族中算法的基本结构是一致的，差别是哈希值的长度、循环运行的次数等略有差异。

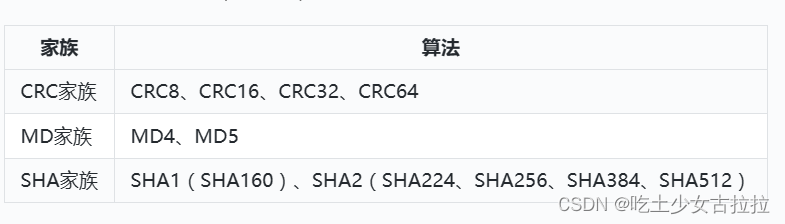
CRC：Cyclic Redundancy [rɪˈdʌndənsi] Check，冗余循环校验算法，主要用于网络数据流的差错校验，检查传输数据的完整性。

MD：Message-Digest Algorithm，消息摘要算法，其中MD5是最常使用的哈希算法。
SHA：Secure Hash Algorithm，安全哈希算法，NIST用于替换MD5的更安全的哈希算法。

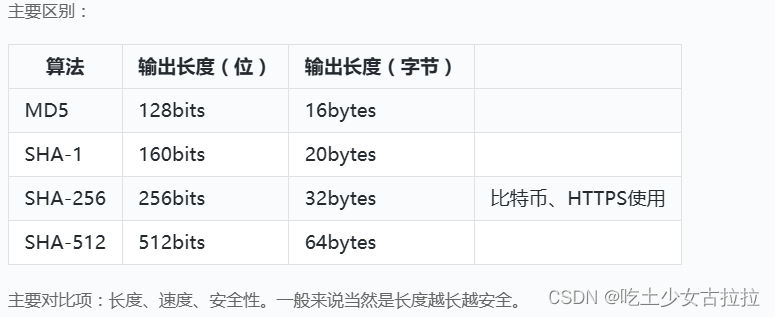
以下是一些哈希算法的应用场景举例：

1. 数据完整性验证：确保文件、消息等在传输或存储过程中没有被篡改。

2. 密码存储：将用户密码进行哈希处理后存储，避免直接存储明文密码。

3. 数字签名：用于生成消息的数字签名，保证消息的真实性和不可否认性。

4. 分布式系统：用于数据的快速查找和定位。

5. 文件系统：用于快速检测文件的重复。