- 1谷歌提出治理开源软件漏洞的新框架:知悉、预防、修复
- 2生成对抗网络(GAN)入门
- 3《大话数据结构》—— 队列的顺序存储结构 (循环队列)—— C++、C# 代码实现_队列的顺序存储代码流程图
- 4ubuntu18.04 安装Teamviewer15出现依赖库出错的解决办法_dpkg: 依赖关系问题使得 teamviewer 的配置工作不能继续: teamviewer 依赖
- 5mysql主从搭建--pxb全备_pxb备份
- 6机器人建模中移动关节如何建立坐标系_机器人标准DH建模法
- 7BUFG/BUFGCE/BUFH/BUFHCE/BUFH/BUFGHCE/BUFMR/BUFMRCE/BUFR/IBUF/IBUFDS
- 8重磅!BRC-20和Solana跨链桥的铭文技术曝光
- 9BPSK调制与解调_bpsk上采样
- 10Python实现通过GUI界面,进行自动化“网络监控”
利用Tensorflow构建CNN图像多分类模型及图像参数、数据维度变化情况实例分析_tensorflow展示cnn分类损失变化
赞
踩
本文以CIFAR-10为数据集,基于Tensorflow介绍了CNN(卷积神经网络)图像分类模型的构建过程,着重分析了在建模过程中卷积层、池化层、扁平化层、全连接层、输出层的运算机理,以及经过运算后图像尺寸、数据维度等参数的变化情况。
CIFAR-10数据集介绍
CIFAR-10数据集由60000张彩色图片构成,其中包括50000张训练集图片、10000张测试集图片,每张图片的shape为(32,32,3),即图片尺寸为32*32,通道数为3;所有图片可以被分为10类,包括:
- 飞机
- 汽车
- 鸟类
- 猫
- 鹿
- 狗
- 青蛙
- 马
- 船只
- 卡车
官网截图如下所示:
利用Tensorflow构建CNN图像多分类模型
TensorFlow™ 是一个使用数据流图进行数值计算的开放源代码软件库,其API可在Python、C++、Java、Go、Swift (Early Release)语言中调用,其中Python API是目前最完整且易用的。TensorFlow擅长训练深度神经网络,被认定为是神经网络中最好用的库之一。通过使用TensorFlow我们可以快速入门神经网络, 大大降低了深度学习(也就是深度神经网络)的开发成本和开发难度。
Tensorflow使用数据流图进行数值计算,图中的节点代表数学运算,图中的边代表在这些节点之间传递的多维数组(张量)。在使用其构建模型时,先搭建好流图结构——类似于铺好管道,然后再加载数据——向管道中注水,让数据在各节点计算、沿各管道流动;数据在流图中计算、传递时采用多维数组(张量)的形式,因此在Tensorflow中参与计算的均为数组数据类型。
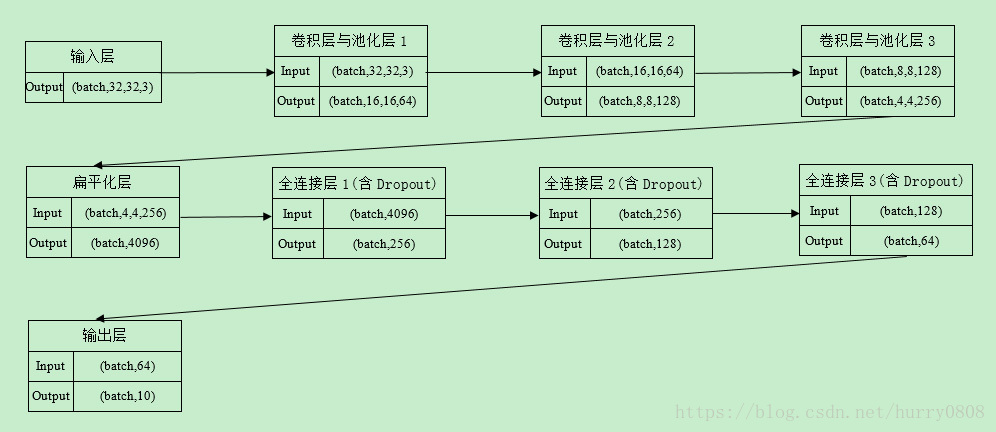
本文使用Tensorflow构建简单的CNN图像多分类模型,其由3个卷积(含激活函数)与池化层、1个扁平层、3个全连接层、1个输出层构成,示意图如下所示:
输入(Input)层
图像数据经过标准化(normalize)、ont-hot编码等预处理后形成的4D张量,本文输入层张量shape为[batch, height, width, channels]。
卷积(Convolution)层
卷积层与池化层的作用在于:
1. invariance(不变性),这种不变性包括translation(平移),rotation(旋转),scale(尺度);
2. 保留主要的特征同时减少参数(降维,效果类似PCA)和计算量,防止过拟合,提高模型泛化能力。
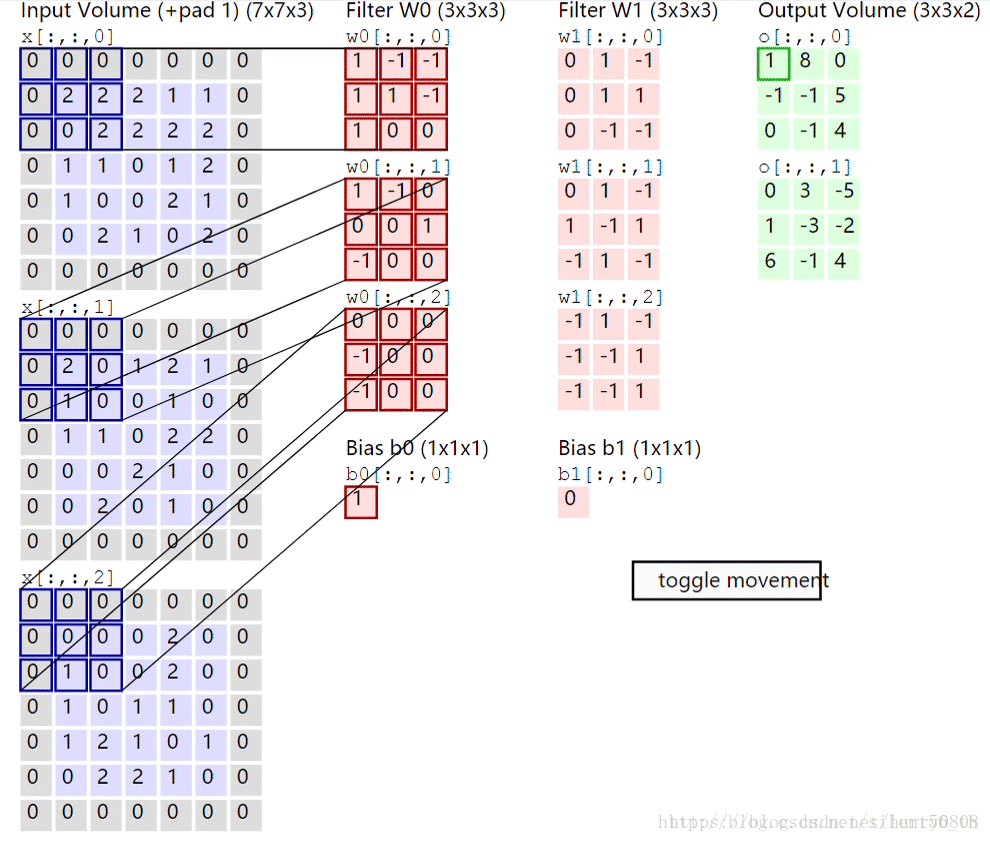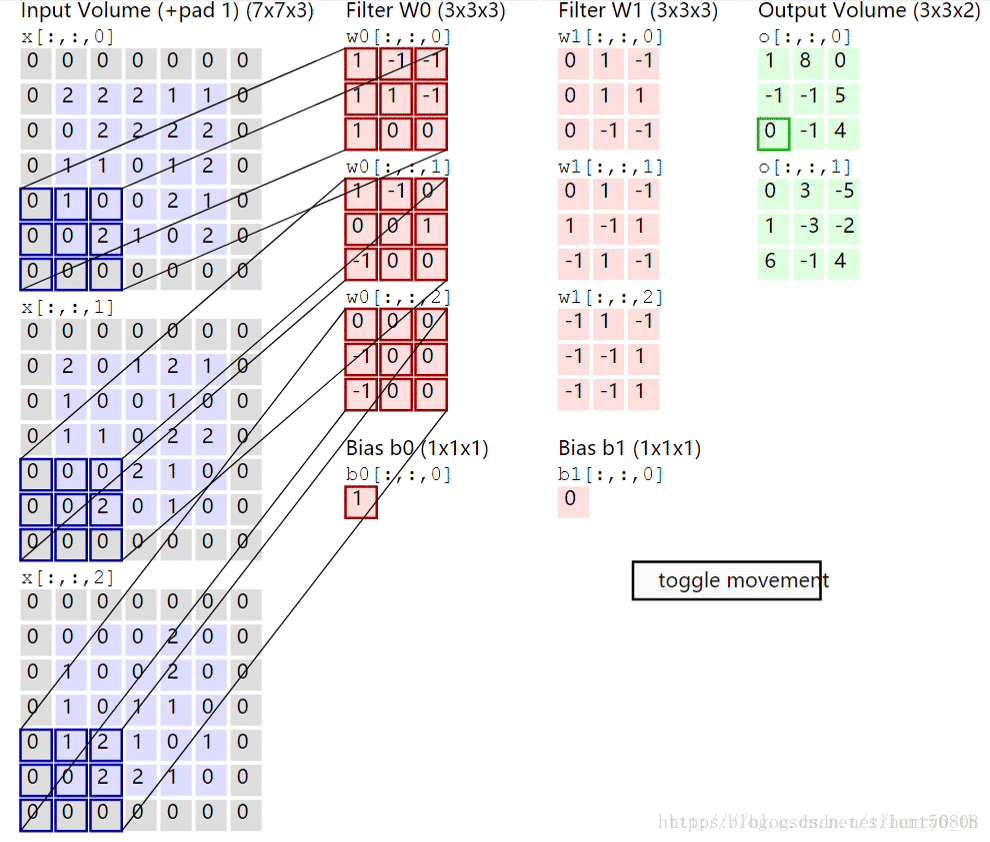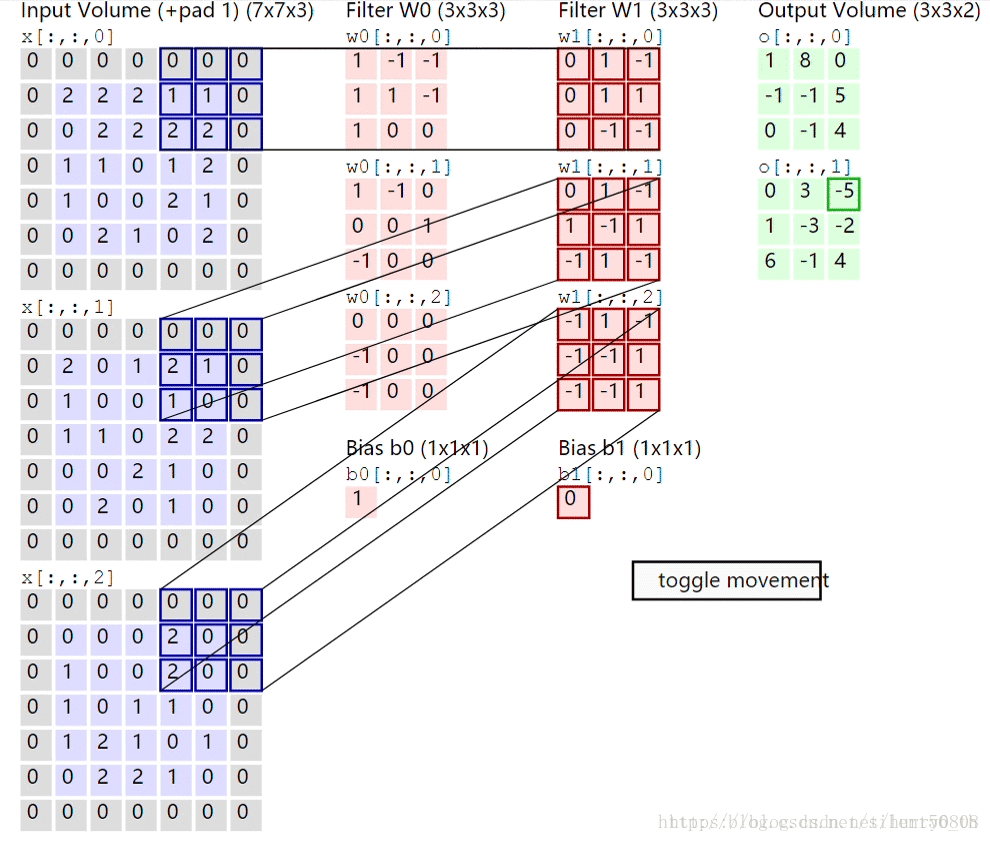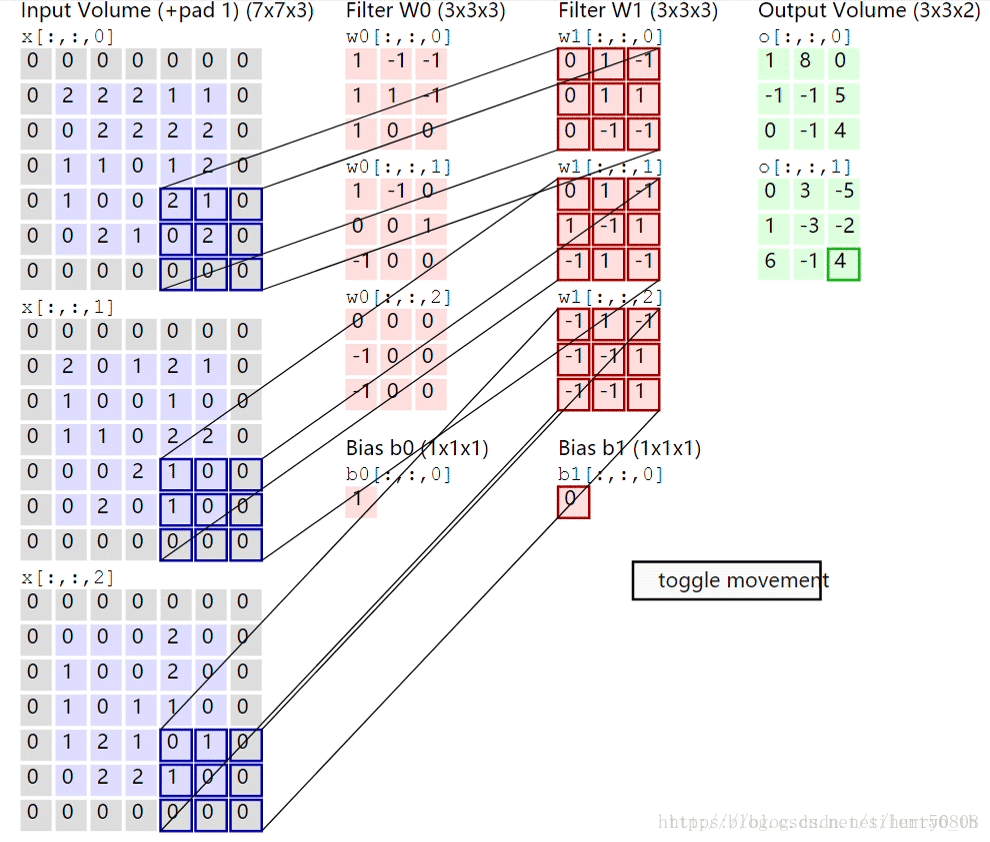
卷积层计算的过程如下图所示:
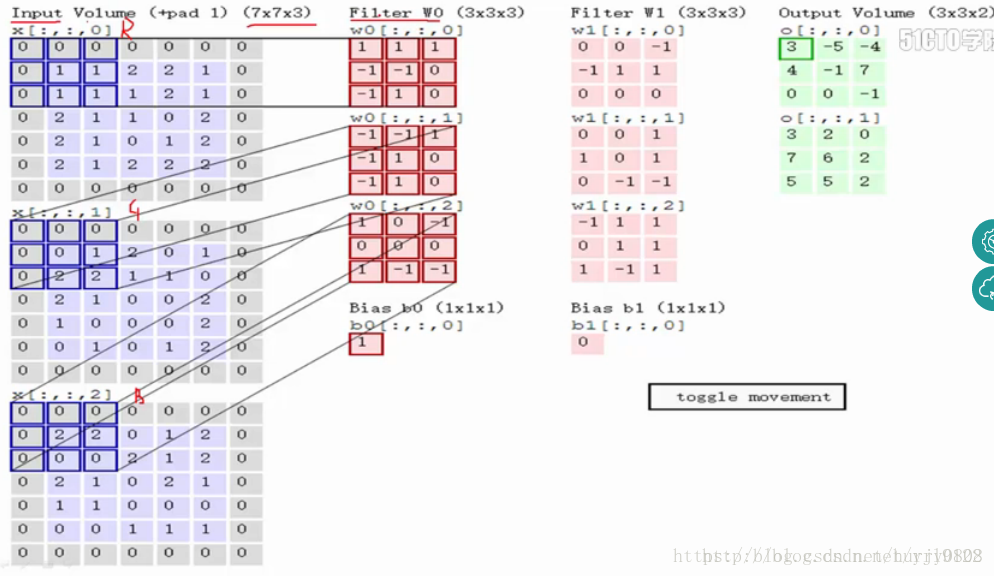
最左侧为输入层图像(加padding后的shape:(7,7,3)),中部为2个卷积核W0、W1及与之相对应的Bias b0、b1,最右侧为输入图像与核w0、w1进行卷积计算后的结果——前者对应于上部图、后者对应于下部图,卷积计算得到的结果即为feature map。每个卷积核与上层图像进行卷积运算后均会得到1个feature map。对于3通道图像,参考本图,卷积运算的过程如下:
1. 输入图像的每个通道分别从左上角开始,每次取与卷积核大小相同的部分(称之为patch),与卷积核对应部分分别相乘后再相加(内积运算);如R通道与W0的最上部核(0核)对应元素相乘再相加得到0,G通道与w0的1核做内积运算得到2,B通道与w0的2核做内积运算后得到0;
2. 内积运算得到的结果相加,再加上w0的bias值(b0),得到feature map左上的元素值;即0+2+0+1=3;
3. 按照指定步长移动卷积核,直至输入图像被整个覆盖,得到最终的feature map;本图中步长(stride)为(2,2)。
这里是动图:
Tensorflow实现卷积运算的函数为:
tf.nn.conv2d(
input,
filter,
strides,
padding,
use_cudnn_on_gpu=True,
data_format='NHWC',
dilations=[1, 1, 1, 1],
name=None
)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
参数说明如下:
- input:需要做卷积的输入图像,它要求是一个Tensor,shape为[batch, in_height, in_width, in_channels],具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数],注意这是一个4维的Tensor,要求类型为float32和float64其中之一;
- filter:相当于CNN中的卷积核,它要求是一个Tensor,shape为[filter_height, filter_width, in_channels, out_channels],具体含义是[卷积核的高度,卷积核的宽度,图像通道数,卷积核个数],要求类型与参数input相同,filter的通道数要求与input的in_channels一致,有一个地方需要注意,第三维in_channels,就是参数input的第四维;
- strides:卷积时在图像每一维的步长,这是一个一维的向量,长度4,strides[0]=strides[3]=1;
- padding:string类型的量,只能是”SAME”、”VALID”其中之一,这个值决定了不同的卷积方式;卷积运算时卷积核滑动过程中当输入图像(input)的in_height、in_width不是filter的filter_height、filter_width的整数倍时,”SAME”方式是在input周围填充0以将其in_height、in_width补充为filter相应部分的整数倍,”VALID”方式将input的多余部分丢弃,详细介绍请参看这里;
- use_cudnn_on_gpu:bool类型,是否使用cudnn加速,默认为true;
- data_format:指定输入数据、输出数据的格式,取值为”NHWC”、”NCHW”,前者对应于 [batch, height, width, channels],后者对应于 [batch, channels, height, width],默认为’NHWC’。
- dilations:一个可选的
ints列表;默认为[1,1,1,1]。长度为4的一维张量,每个input维度的膨胀系数; 如果设置为k> 1,则每个该维度上的过滤器元素之间会有k-1个跳过的单元格; 维度顺序由data_format的值决定; 在Dilations中批次和深度尺寸必须为1; - name:为该操作指定名称;
- 返回值:Tensor,也就是我们常说的feature map。
输入图像经过卷积运算后,其高度、宽度变为——
‘SAME’ 类型的padding,其输出的height和width计算如下:
out_height = ceil(float(in_height) / float(strides[1])) ceil:向上取整
out_width = ceil(float(in_width) / float(strides[2]))
‘VALID’类型的padding, 其输出的height和width计算如下:
out_height = ceil(float(in_height – filter_height + 1) / float(strides[1]))
out_width = ceil(float(in_width – filter_width + 1) / float(strides[2]))
验证该函数的文章,请看这里。
激活函数(Activation Function)
池化层、全连接层等通过线性运算构建的是线性模型,该模型的表达能力有限;激活函数能够加入非线性因素,从而使模型的表达能力得到极大提升。常用的激活函数有Tanh函数 、ReLU函数 、Leaky ReLU函数 、Maxout函数 等,本文使用ReLU函数作为激活函数。
Tensorflow中的relu激活函数为:
tf.nn.relu(
features,
name=None
)
- 1
- 2
- 3
- 4
- 5
参数说明如下:
- features: 张量,必须为以下类型中的一种: float32, float64, int32, uint8, int16, int8, int64, bfloat16, uint16, half, uint32, uint64;
- name: 为该操作指定名称;
- Returns: 张量。
池化(Pooling)层
池化层与卷积层的作用、计算方法类似,也有池化filter、步长、填充方式等参数,所不同的是,池化计算比较简单,常取filter覆盖部分的最大值、或者均值,分别称之为最大池化、平均池化,最大池化的示意图如下所示:
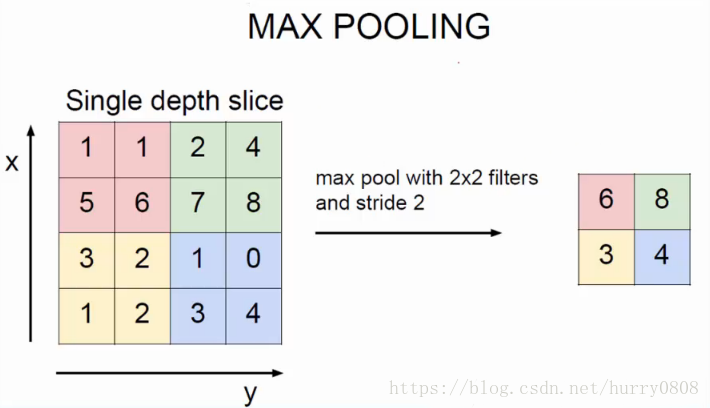
最大池化的filter shape为(2,2), 步长也为(2,2),每个filter滑动覆盖处取最大值,得到右侧所示的结果。
Tensorflow实现最大池化运算的函数为:
tf.nn.max_pool(
value,
ksize,
strides,
padding,
data_format='NHWC',
name=None
)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
参数说明如下:
- value:输入4D张量, 其格式由data_format指定;
- ksize:含有4个元素的1D张量,指定池化核的尺寸;
- strides:含有4个元素的1D int 张量,指定池化时在图像每一维的步长,strides[0]=strides[3]=1;
- padding: 边界填充方式,string类型的量,只能是”SAME”、”VALID”其中之一;
- data_format:数据格式,string类型的量, 只能是’NHWC’、 ‘NCHW’ 、’NCHW_VECT_C’ 其中之一;
- name:为该操作指定名称;
- 返回值: Tensor,也就是我们常说的feature map。
上层feature map经池化运算后,其batch、channels均不发生变化,只有height、width会发生变化,输出height、width计算方式同卷积层。
扁平化(Flatten)层
将上一层得到的全部feature map拉直成列向量,作为全连接网络的输入。拉直方式为height*width*channels。
Tensorflow实现扁平化层运算的函数为:
tf.contrib.layers.flatten(
inputs,
outputs_collections=None,
scope=None
)- 1
- 2
- 3
- 4
- 5
参数说明如下:
- inputs:形如 [batch_size, …]的张量,注意张量的第1个元素必须为batch_size;
- outputs_collections:添加到输出的集合;
- scope:name_scope的可选范围。
- 返回值:形如[batch_size, k]的扁平化张量。
图像分类模型训练完成后,本层返回张量的shape(主要是k)就确定了,从而限定了模型预测时输入图像的尺寸——因为在模型确定的情况下,卷积层、池化层等结构、数量均不再改变,预测图像与训练图像尺寸一致时,经卷积、池化等运算后,扁平化输出shape与模型一致;预测图像与训练图像尺寸不一致时,经卷积、池化等运算后,扁平化输出的shape与模型不一致,从而无法继续运算。这也是迁移学习时,预训练模型均约定输入图像height、width的原因。
从该层开始,分类模型的网络结构类似于“多层前馈神经网络”。
全连接(Fully Connected)层
全连接层在整个卷积神经网络中起到“分类器”的作用、也是模型表示能力的“防火墙”。全连接层的运算形如X*W+b,X*W为矩阵乘法,其中X为输入2维数组(shape为[batch_size, k]),W为权重2维数组(shape为[k,out_k]),b为偏置,W的第2个元素(out_k)决定了全连接层运算后输出的2维数组形状(shape为[batch_size, out_k])。
由于全连接层参数冗余(仅全连接层参数就可占整个网络参数80%左右),需要使用tf.nn.dropout来随机丢弃一些节点,或者使用一些性能优异的网络模型如ResNet和GoogLeNet等来取代全连接层融合学到的深度特征。
Tensorflow中实现全连接层的函数为:
tf.layers.dense(
inputs,
units,
activation=None,
use_bias=True,
kernel_initializer=None,
bias_initializer=tf.zeros_initializer(),
kernel_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
bias_constraint=None,
trainable=True,
name=None,
reuse=None
)

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
参数说明如下:
- inputs: Tensor input.
- units: Integer or Long, dimensionality of the output space.
- activation: Activation function (callable). Set it to None to maintain a linear activation.
- use_bias: Boolean, whether the layer uses a bias.
- kernel_initializer: Initializer function for the weight matrix. If None (default), weights are initialized using the default initializer used by tf.get_variable.
- bias_initializer: Initializer function for the bias.
- kernel_regularizer: Regularizer function for the weight matrix.
- bias_regularizer: Regularizer function for the bias.
- activity_regularizer: Regularizer function for the output.
- kernel_constraint: An optional projection function to be applied to the kernel after being updated by an Optimizer (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected variable and must return the projected variable (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
- bias_constraint: An optional projection function to be applied to the bias after being updated by an Optimizer.
- trainable: Boolean, if True also add variables to the graph collection GraphKeys.TRAINABLE_VARIABLES (see tf.Variable).
- name: String, the name of the layer.
- reuse: Boolean, whether to reuse the weights of a previous layer by the same name.
- Returns:Output tensor the same shape as inputs except the last dimension is of size units.
Tensorflow中的Dropout函数为:
tf.nn.dropout(
x,
keep_prob,
noise_shape=None,
seed=None,
name=None
)- 1
- 2
- 3
- 4
- 5
- 6
- 7
参数说明:
- x: A floating point tensor.
- keep_prob: A scalar Tensor with the same type as x. The probability that each element is kept.
- noise_shape: A 1-D Tensor of type int32, representing the shape for randomly generated keep/drop flags.
- seed: A Python integer. Used to create random seeds. See tf.set_random_seed for behavior.
- name: A name for this operation (optional).
- Returns: A Tensor of the same shape of x.
输出(Output)层
输出层运算与全连接层类似,只是在设定运算参数时输出节点数量需与分类标记数量相一致,并且在运算完成后再使用tf.nn.softmax函数,得到测试图像属于各分类的概率,该所有概率值之和为1。
Tensorflow中的tf.nn.softmax函数如下所示:
tf.nn.softmax(
logits,
axis=None,
name=None,
dim=None
)- 1
- 2
- 3
- 4
- 5
- 6
参数说明如下:
- logits: A non-empty Tensor. Must be one of the following types: half, float32, float64.
- axis: The dimension softmax would be performed on. The default is -1 which indicates the last dimension.
- name: A name for the operation (optional).
- dim: Deprecated alias for axis.
- Returns: A Tensor. Has the same type and shape as logits.
训练得到分类模型
按照输入层、卷积层与池化层(共3层)、扁平化层、全连接层(共3层)、输出层的顺序搭建好模型,以交叉熵均值作为cost,以Adam优化算法寻找全局最优点,以cost、Accuracy(分类准确率)作为评估模型的指标,各层参数设置如下图所示:
补充说明如下:
- batch为训练时每批输入的图像数量,视训练环境的硬件配置而定,本文设置为512
- 卷积核height,width:(3,3)
- 卷积步长:(1,1,1,1)
- 卷积 padding:SAME
- 激活函数:tf.nn.relu
- 最大池化height,width:(2,2)
- 最大池化步长:(1,2,2,1)
- 池化 padding:SAME
- Dropout时保留节点的比例:0.5
- Epochs(训练轮数):30
训练构建好的CNN图像分类模型时,单张图片用3D数组表示,多张图片用4D数组表示,经过卷积、激活函数、池化、扁平化、全连接、Dropout等运算,其batch、height、width、channels、feature map数量、节点数量、数据shape有的会发生变化,有的不会发生变化,如下表所示:
| 运算名称 | batch | 图像height | 图像width | 图像channels | feature map数量 | 节点数量 | 数据shape |
|---|---|---|---|---|---|---|---|
| 卷积 | 不改变 | 会改变 | 会改变 | (首次卷积后变成1) | 会改变 | - | 4D张量 |
| 激活函数 | 不改变 | 不改变 | 不改变 | - | 不改变 | - | 4D张量 |
| 池化 | 不改变 | 会改变 | 会改变 | - | 不改变 | - | 4D张量 |
| 扁平化 | 不改变 | 不改变 | 不改变 | - | 不改变 | 不改变 | 2D张量 |
| 全连接 | 不改变 | - | - | - | - | 会改变 | 2D张量 |
| Dropout | 不改变 | - | - | - | - | 会改变 | 2D张量 |
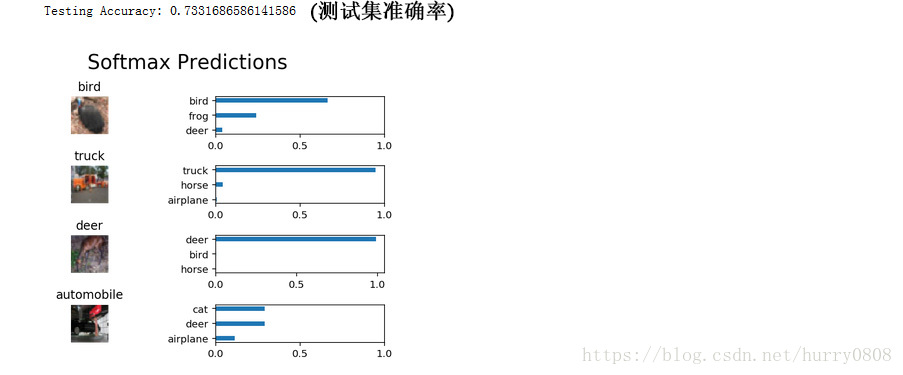
使用CIFAR-10训练集进行训练,在训练集和测试集上的准确率均为0.73,如下图所示:
小结
本文以CIFAR-10数据集为例,使用Tensorflow构建了简单的CNN图像分类模型,该模型包含输入层、卷积与池化层、扁平化层、全连接层、输出层,这些层均是构建CNN分类模型必要且重要的层;训练后分类模型的准确率虽然不够高,但本文重在分析各层运算时图像数据shape的变化及其它尺寸数据的改变情况。