实验四 Apriori / k-Means算法实现_apriori 算法实验目的
赞
踩
一、实验目的
1、掌握Apriori/k-Means算法。
2、掌握关联或分类的方法。
3、掌握C/C++、python等的用法。
二、实验内容
我们进行交易的数据项见下表所示,预定义最小支持度minsupport=2。
| TID | Items |
| T1 | I1,I3,I4 |
| T2 | I2,I3,I5 |
| T3 | I1,I2,I3,I5 |
| T4 | I2,I5 |
此实验为综合型实验,要求学生综合利用先修课程高级程序设计语言、数据库、算法设计与分析,与本门数据挖掘课程的知识,选择一种编程工具,实现经典挖掘算法Apriori算法和k-Means。
三、实验原理
Apriori算法是第一个关联规则挖掘算法,也是最经典的算法。它利用逐层搜索的迭代方法找出数据库中项集的关系,以形成规则,其过程由连接(类矩阵运算)与剪枝(去掉那些没必要的中间结果)组成。该算法中项集的概念即为项的集合。包含K个项的集合为k项集。项集出现的频率是包含项集的事务数,称为项集的频率。如果某项集满足最小支持度,则称它为频繁项集。
该算法的基本思想是:首先找出所有的频集,这些项集出现的频繁性至少和预定义的最小支持度一样。然后由频集产生强关联规则,这些规则必须满足最小支持度和最小可信度。然后使用第1步找到的频集产生期望的规则,产生只包含集合的项的所有规则,其中每一条规则的右部只有一项,这里采用的是中规则的定义。一旦这些规则被生成,那么只有那些大于用户给定的最小可信度的规则才被留下来。为了生成所有频集,使用了递归的方法。
但其有一些难以克服的缺点:
(1)对数据库的扫描次数过多。
(2)Apriori算法会产生大量的中间项集。
(3)采用唯一支持度。
(4)算法的适应面窄。
Kmeans
先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了,每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个:
1)没有(或最小数目)对象被重新分配给不同的聚类。
2)没有(或最小数目)聚类中心再发生变化。
3)误差平方和局部最小。
伪代码
选择k个点作为初始质心。
repeat 将每个点指派到最近的质心,形成k个簇 重新计算每个簇的质心 until 质心不发生变化
实验代码
Dashuju4.py
- 1.min_sup = 2
- 2.min_conf = 0.6
- 3.# 最大 K 项集
- 4.K = 3
- 5.
- 6.def apriori():
- 7. data_set = load_data()
- 8. C1 = create_C1(data_set)
- 9. item_count = count_itemset1(data_set, C1)
- 10. L1 = generate_L1(item_count)
- 11. Lk_copy = L1.copy()
- 12. L = []
- 13. L.append(Lk_copy)
- 14. for i in range(2, K + 1):
- 15. Ci = create_Ck(Lk_copy, i)
- 16. Li = generate_Lk_by_Ck(Ci, data_set)
- 17. Lk_copy = Li.copy()
- 18. L.append(Lk_copy)
- 19.
- 20. print('频繁项集\t支持度计数')
- 21. support_data = {}
- 22. for item in L:
- 23. for i in item:
- 24. print(list(i), '\t', item[i])
- 25. support_data[i] = item[i]
- 26.
- 27. strong_rules_list = generate_strong_rules(L, support_data, data_set)
- 28. strong_rules_list.sort(key=lambda result: result[2], reverse=True)
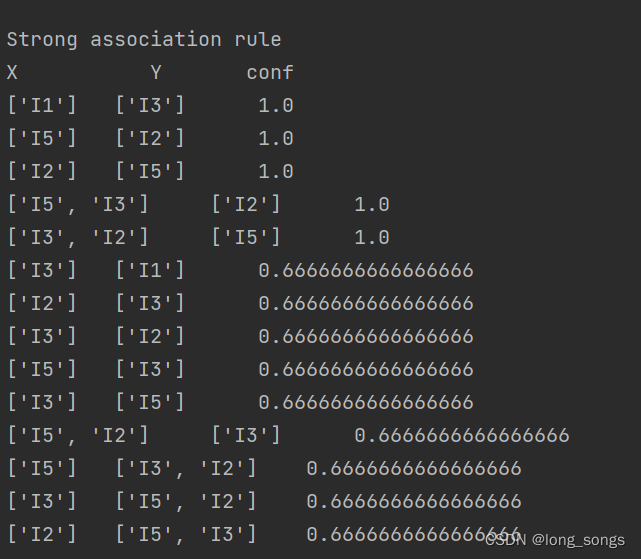
- 29. print("\nStrong association rule\nX\t\t\tY\t\tconf")
- 30. for item in strong_rules_list:
- 31. print(list(item[0]), "\t", list(item[1]), "\t", item[2])
- 32.
- 33.
- 34.
- 35.def load_data():
- 36.
- 37. data = {'001': 'I1,I3,I4', '002': 'I2,I3,I5',
- 38. '003': 'I1,I2,I3,I5', '004': 'I2,I5'}
- 39. data_set = []
- 40. for key in data:
- 41. item = data[key].split(',')
- 42. data_set.append(item)
- 43. return data_set
- 44.
- 45.
- 46.def create_C1(data_set):
- 47. C1 = set()
- 48. for t in data_set:
- 49. for item in t:
- 50. item_set = frozenset([item])
- 51. C1.add(item_set)
- 52. return C1
- 53.
- 54.
- 55.def count_itemset1(data_set, C1):
- 56. item_count = {}
- 57. for data in data_set:
- 58. for item in C1:
- 59. if item.issubset(data):
- 60. if item in item_count:
- 61. item_count[item] += 1
- 62. else:
- 63. item_count[item] = 1
- 64. return item_count
- 65.
- 66.
- 67.def generate_L1(item_count):
- 68. L1 = {}
- 69. for i in item_count:
- 70. if item_count[i] >= min_sup:
- 71. L1[i] = item_count[i]
- 72. return L1
- 73.
- 74.
- 75.def is_apriori(Ck_item, Lk_copy):
- 76. for item in Ck_item:
- 77. sub_Ck = Ck_item - frozenset([item])
- 78. if sub_Ck not in Lk_copy:
- 79. return False
- 80. return True
- 81.
- 82.
- 83.def create_Ck(Lk_copy, k):
- 84. Ck = set()
- 85. len_Lk_copy = len(Lk_copy)
- 86. list_Lk_copy = list(Lk_copy)
- 87. for i in range(len_Lk_copy):
- 88. for j in range(1, len_Lk_copy):
- 89. l1 = list(list_Lk_copy[i])
- 90. l2 = list(list_Lk_copy[j])
- 91. l1.sort()
- 92. l2.sort()
- 93. if l1[0:k-2] == l2[0:k-2]:
- 94. Ck_item = list_Lk_copy[i] | list_Lk_copy[j]
- 95. if is_apriori(Ck_item, Lk_copy):
- 96. Ck.add(Ck_item)
- 97. return Ck
- 98.
- 99.
- 100.def generate_Lk_by_Ck(Ck, data_set):
- 101. item_count = {}
- 102. for data in data_set:
- 103. for item in Ck:
- 104. if item.issubset(data):
- 105. if item in item_count:
- 106. item_count[item] += 1
- 107. else:
- 108. item_count[item] = 1
- 109. Lk2 = {}
- 110. for i in item_count:
- 111. if item_count[i] >= min_sup:
- 112. Lk2[i] = item_count[i]
- 113. return Lk2
- 114.
- 115.
- 116.def generate_strong_rules(L, support_data, data_set):
- 117. strong_rule_list = []
- 118. sub_set_list = []
- 119. # print(L)
- 120. for i in range(0, len(L)):
- 121. for freq_set in L[i]:
- 122. for sub_set in sub_set_list:
- 123. if sub_set.issubset(freq_set):
- 124. # 计算包含 X 的交易数
- 125. sub_set_num = 0
- 126. for item in data_set:
- 127. if (freq_set - sub_set).issubset(item):
- 128. sub_set_num += 1
- 129. conf = support_data[freq_set] / sub_set_num
- 130. strong_rule = (freq_set - sub_set, sub_set, conf)
- 131. if conf >= min_conf and strong_rule not in strong_rule_list:
- 132. # print(list(freq_set-sub_set), " => ", list(sub_set), "conf: ", conf)
- 133. strong_rule_list.append(strong_rule)
- 134. sub_set_list.append(freq_set)
- 135. return strong_rule_list
- 136.
- 137.
- 138.if __name__ == '__main__':
- 139. apriori()

可视化代码
- 1.# coding=utf-8
- 2.min_sup = 2
- 3.min_conf = 0.6
- 4.# 最大 K 项集
- 5.K = 3
- 6.import matplotlib.pyplot as plt
- 7.import numpy as np
- 8.def apriori():
- 9. data_set = load_data()
- 10. C1 = create_C1(data_set)
- 11. item_count = count_itemset1(data_set, C1)
- 12. L1 = generate_L1(item_count)
- 13. Lk_copy = L1.copy()
- 14. L = []
- 15. L.append(Lk_copy)
- 16. for i in range(2, K + 1):
- 17. Ci = create_Ck(Lk_copy, i)
- 18. Li = generate_Lk_by_Ck(Ci, data_set)
- 19. Lk_copy = Li.copy()
- 20. L.append(Lk_copy)
- 21.
- 22. print('频繁项集\t支持度计数')
- 23. a = [[],[]]
- 24. z = [[],[],[]]
- 25. cla = []
- 26. support_data = {}
- 27. for item in L:
- 28. for i in item:
- 29. print(list(i), '\t', item[i])
- 30. a[0].append(str(list(i)))
- 31. a[1].append(str(item[i]))
- 32. support_data[i] = item[i]
- 33. cla.append(str(i))
- 34. strong_rules_list = generate_strong_rules(L, support_data, data_set)
- 35. strong_rules_list.sort(key=lambda result: result[2], reverse=True)
- 36. print("\nStrong association rule\nX\t\t\tY\t\tconf")
- 37. print([0])
- 38. for item in strong_rules_list:
- 39. print(list(item[0]), "\t", list(item[1]), "\t", item[2])
- 40. # 设置x/y轴尺度
- 41.
- 42. plt.ylim(0,4)
- 43. for i in range(len(a[0])):
- 44. plt.bar(a[0][i], int(a[1][i]), label=cla[i], width=1)
- 45.
- 46. plt.legend()
- 47. plt.xlabel('number')
- 48. plt.ylabel('value')
- 49.
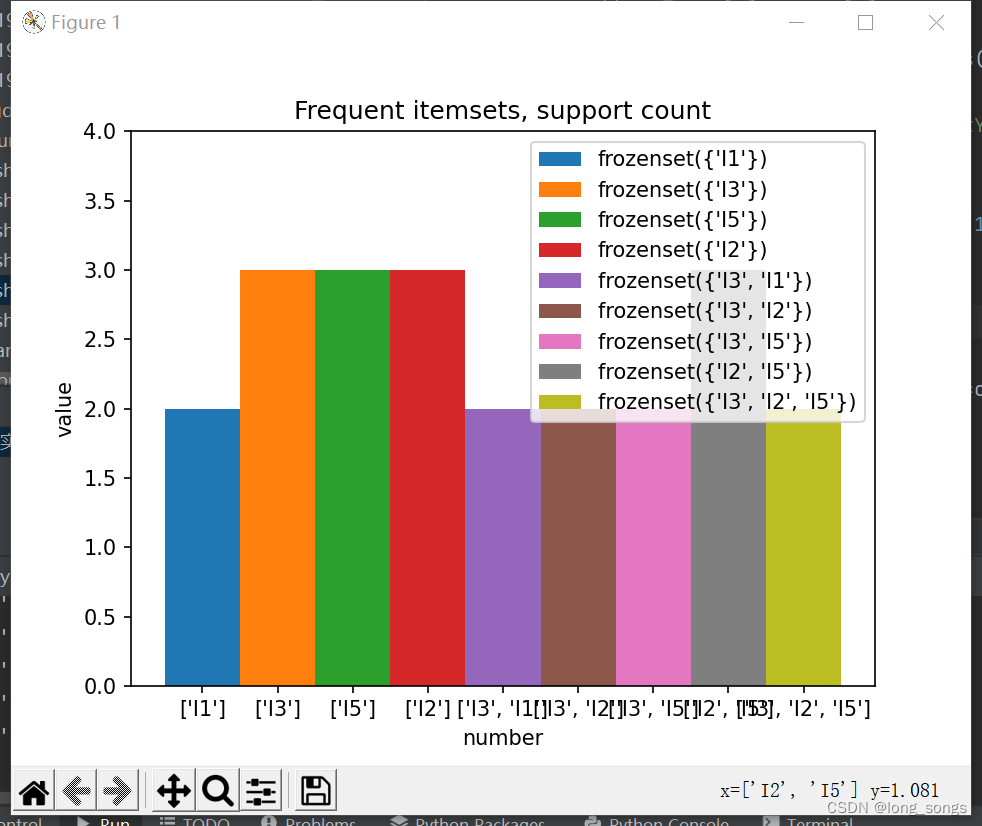
- 50. plt.title("Frequent itemsets, support count")
- 51.
- 52. plt.show()
- 53. for item in strong_rules_list:
- 54. print(list(item[0]), "\t", list(item[1]), "\t", item[2])
- 55. z[0].append(str(list(item[0])))
- 56. z[1].append(str(list(item[1])))
- 57. z[2].append(item[2])
- 58. # 表示随机生成一个标准正态分布形状是600*2的数组
- 59. plt.figure(figsize=(8, 5)) # 表示绘制图形的画板尺寸为8*5
- 60.
- 61. # 表示随机生成一个第三维度的数据集,取值在0-10之间的整数
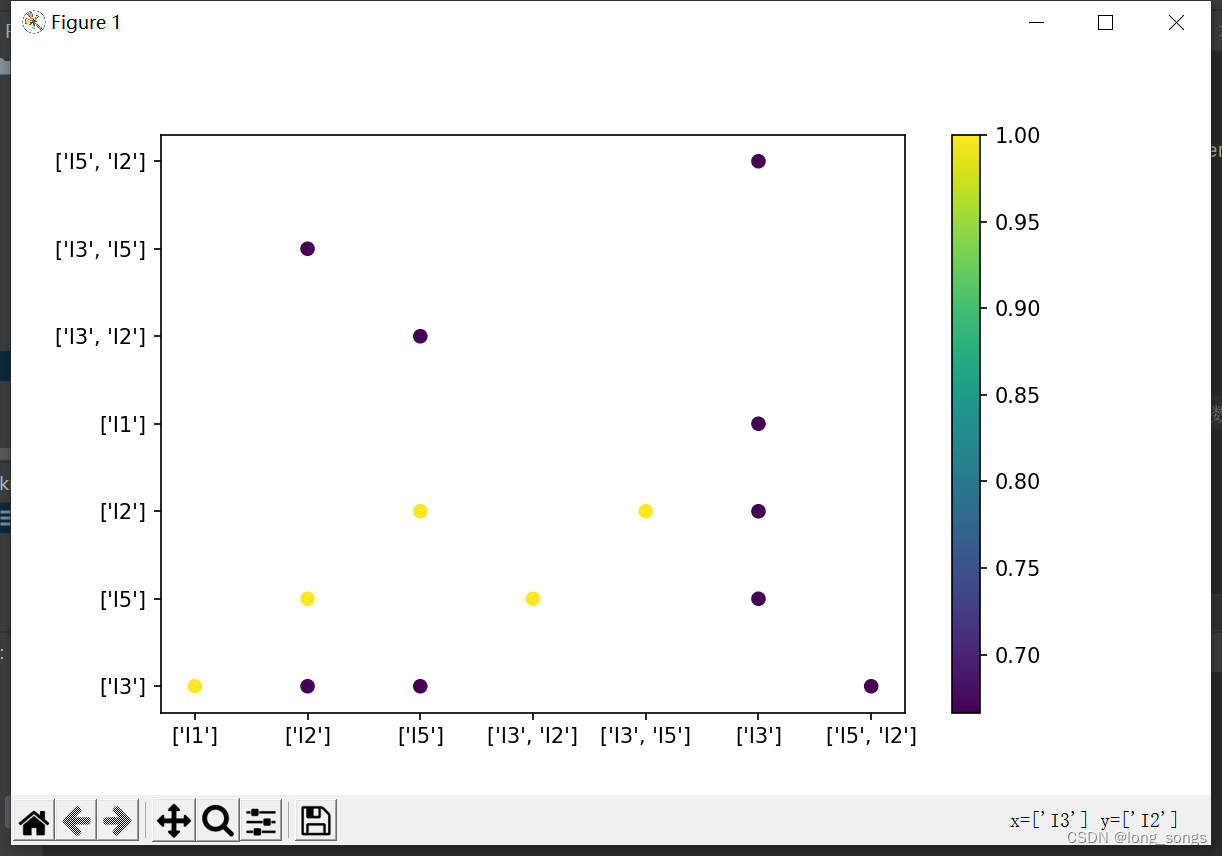
- 62. plt.scatter(z[0], z[1], c=z[2], marker='o') # 表示颜色数据来源于第三维度的c
- 63. plt.colorbar()
- 64. plt.show()
- 65.
- 66.def load_data():
- 67.
- 68. data = {'001': 'I1,I3,I4', '002': 'I2,I3,I5',
- 69. '003': 'I1,I2,I3,I5', '004': 'I2,I5'}
- 70. data_set = []
- 71. for key in data:
- 72. item = data[key].split(',')
- 73. data_set.append(item)
- 74. return data_set
- 75.
- 76.
- 77.def create_C1(data_set):
- 78. C1 = set()
- 79. for t in data_set:
- 80. for item in t:
- 81. item_set = frozenset([item])
- 82. C1.add(item_set)
- 83. return C1
- 84.
- 85.
- 86.def count_itemset1(data_set, C1):
- 87. item_count = {}
- 88. for data in data_set:
- 89. for item in C1:
- 90. if item.issubset(data):
- 91. if item in item_count:
- 92. item_count[item] += 1
- 93. else:
- 94. item_count[item] = 1
- 95. return item_count
- 96.
- 97.
- 98.def generate_L1(item_count):
- 99. L1 = {}
- 100. for i in item_count:
- 101. if item_count[i] >= min_sup:
- 102. L1[i] = item_count[i]
- 103. return L1
- 104.
- 105.
- 106.def is_apriori(Ck_item, Lk_copy):
- 107. for item in Ck_item:
- 108. sub_Ck = Ck_item - frozenset([item])
- 109. if sub_Ck not in Lk_copy:
- 110. return False
- 111. return True
- 112.
- 113.
- 114.def create_Ck(Lk_copy, k):
- 115. Ck = set()
- 116. len_Lk_copy = len(Lk_copy)
- 117. list_Lk_copy = list(Lk_copy)
- 118. for i in range(len_Lk_copy):
- 119. for j in range(1, len_Lk_copy):
- 120. l1 = list(list_Lk_copy[i])
- 121. l2 = list(list_Lk_copy[j])
- 122. l1.sort()
- 123. l2.sort()
- 124. if l1[0:k-2] == l2[0:k-2]:
- 125. Ck_item = list_Lk_copy[i] | list_Lk_copy[j]
- 126. if is_apriori(Ck_item, Lk_copy):
- 127. Ck.add(Ck_item)
- 128. return Ck
- 129.
- 130.
- 131.def generate_Lk_by_Ck(Ck, data_set):
- 132. item_count = {}
- 133. for data in data_set:
- 134. for item in Ck:
- 135. if item.issubset(data):
- 136. if item in item_count:
- 137. item_count[item] += 1
- 138. else:
- 139. item_count[item] = 1
- 140. Lk2 = {}
- 141. for i in item_count:
- 142. if item_count[i] >= min_sup:
- 143. Lk2[i] = item_count[i]
- 144. return Lk2
- 145.
- 146.
- 147.def generate_strong_rules(L, support_data, data_set):
- 148. strong_rule_list = []
- 149. sub_set_list = []
- 150. # print(L)
- 151. for i in range(0, len(L)):
- 152. for freq_set in L[i]:
- 153. for sub_set in sub_set_list:
- 154. if sub_set.issubset(freq_set):
- 155. # 计算包含 X 的交易数
- 156. sub_set_num = 0
- 157. for item in data_set:
- 158. if (freq_set - sub_set).issubset(item):
- 159. sub_set_num += 1
- 160. conf = support_data[freq_set] / sub_set_num
- 161. strong_rule = (freq_set - sub_set, sub_set, conf)
- 162. if conf >= min_conf and strong_rule not in strong_rule_list:
- 163. # print(list(freq_set-sub_set), " => ", list(sub_set), "conf: ", conf)
- 164. strong_rule_list.append(strong_rule)
- 165. sub_set_list.append(freq_set)
- 166. return strong_rule_list
- 167.
- 168.
- 169.if __name__ == '__main__':
- 170. apriori()

kmeans 分类
- 1.import random
- 2.import pandas as pd
- 3.import numpy as np
- 4.import matplotlib.pyplot as plt
- 5.
- 6.
- 7.# 计算欧拉距离
- 8.def calcDis(dataSet, centroids, k):
- 9. clalist = []
- 10. for data in dataSet:
- 11. diff = np.tile(data, (k,
- 12. 1)) - centroids # 相减 (np.tile(a,(2,1))就是把a先沿x轴复制1倍,即没有复制,仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))
- 13. squaredDiff = diff ** 2 # 平方
- 14. squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)
- 15. distance = squaredDist ** 0.5 # 开根号
- 16. clalist.append(distance)
- 17. clalist = np.array(clalist) # 返回一个每个点到质点的距离len(dateSet)*k的数组
- 18. return clalist
- 19.
- 20.
- 21.# 计算质心
- 22.def classify(dataSet, centroids, k):
- 23. # 计算样本到质心的距离
- 24. clalist = calcDis(dataSet, centroids, k)
- 25. # 分组并计算新的质心
- 26. minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标
- 27. newCentroids = pd.DataFrame(dataSet).groupby(
- 28. minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值
- 29. newCentroids = newCentroids.values
- 30.
- 31. # 计算变化量
- 32. changed = newCentroids - centroids
- 33.
- 34. return changed, newCentroids
- 35.
- 36.
- 37.# 使用k-means分类
- 38.def kmeans(dataSet, k):
- 39. # 随机取质心
- 40. centroids = random.sample(dataSet, k)
- 41.
- 42. # 更新质心 直到变化量全为0
- 43. changed, newCentroids = classify(dataSet, centroids, k)
- 44. while np.any(changed != 0):
- 45. changed, newCentroids = classify(dataSet, newCentroids, k)
- 46.
- 47. centroids = sorted(newCentroids.tolist()) # tolist()将矩阵转换成列表 sorted()排序
- 48.
- 49. # 根据质心计算每个集群
- 50. cluster = []
- 51. clalist = calcDis(dataSet, centroids, k) # 调用欧拉距离
- 52. minDistIndices = np.argmin(clalist, axis=1)
- 53. for i in range(k):
- 54. cluster.append([])
- 55. for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素
- 56. cluster[j].append(dataSet[i])
- 57.
- 58. return centroids, cluster
- 59.
- 60.
- 61.# 创建数据集
- 62.def createDataSet():
- 63. return [[1, 1], [1, 2], [2, 2], [1, 3], [3, 3], [4, 2], [5, 3], [6, 3], [6, 2], [6, 4], [7, 1], [2, 5], [3, 6], [6, 7]]
- 64.
- 65.
- 66.if __name__ == '__main__':
- 67. dataset = createDataSet()
- 68. centroids, cluster = kmeans(dataset, 2)
- 69. print('质心为:%s' % centroids)
- 70. print('集群为:%s' % cluster)
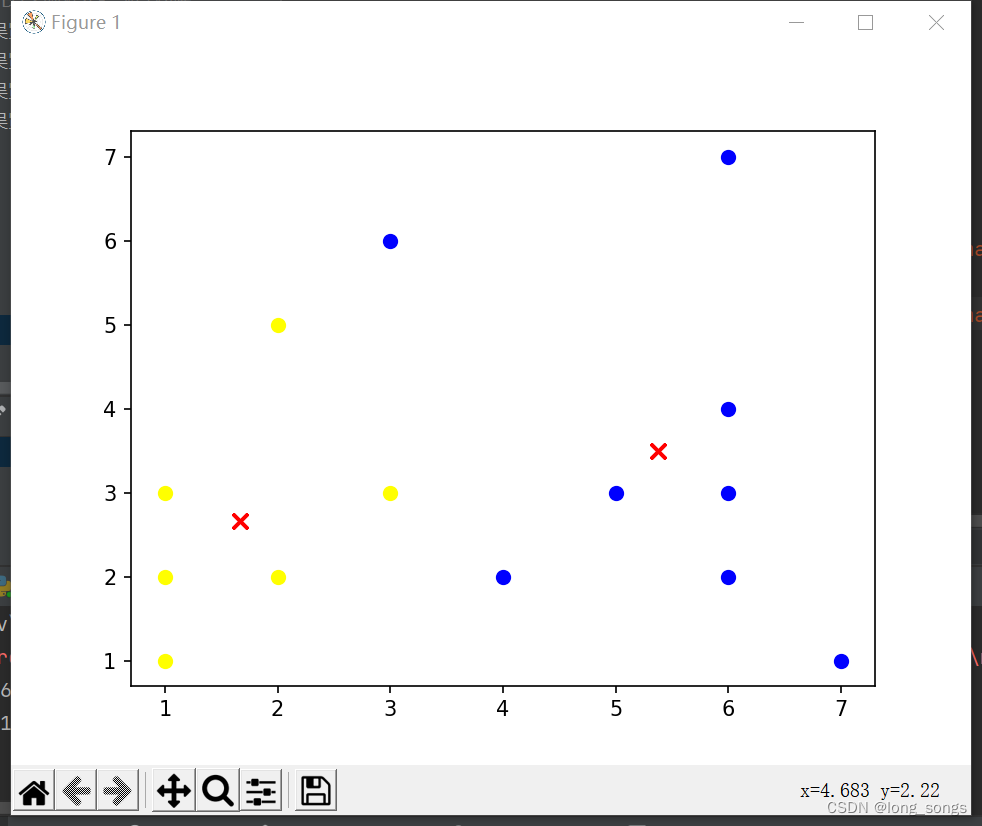
- 71. for i in range(len(dataset)):
- 72. for j in range(len(centroids)):
- 73. plt.scatter(centroids[j][0], centroids[j][1], marker='x', color='red', s=50, label='质心')
- 74. for i in range(len(cluster[0])):
- 75. plt.scatter(cluster[0][i][0], cluster[0][i][1], marker='o', color='yellow', s=40, label='shenzu')
- 76. for j in range(len(cluster[1])):
- 77. plt.scatter(cluster[1][j][0], cluster[1][j][1], marker='o', color='blue', s=40, label='qizu')
- 78. plt.show()

运行结果图: