KAN神经网络 | KAN和MLP比较

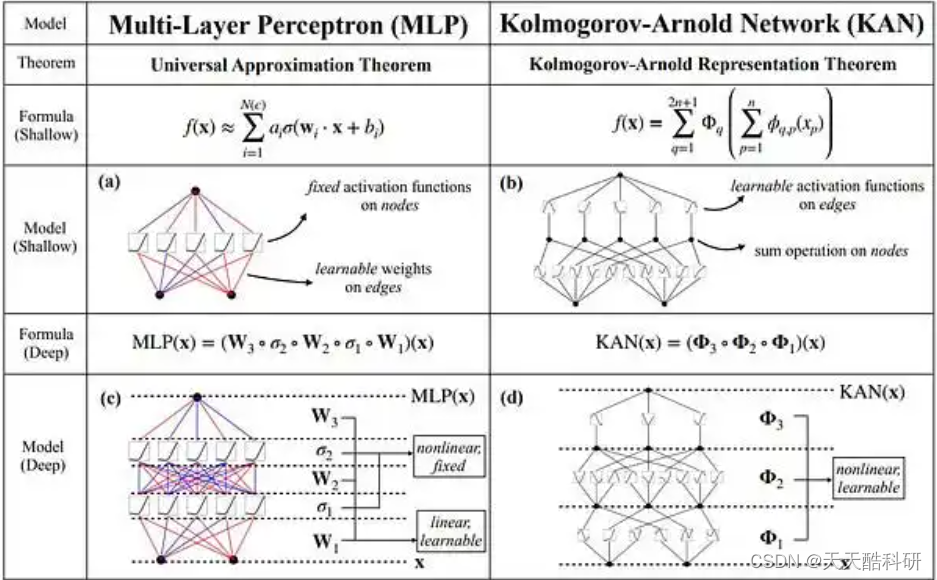
首先，让我们快速概述一下 KAN 及其实现的理论：

柯尔莫哥洛夫-阿诺德表示定理：

我们跳过繁琐的公式和定义，只用一个简单的解释。KART指出，

任何具有多个输入的连续函数都可以通过组合单个输入的简单函数（如正弦或平方）并将它们相加来创建。

例如，多元函数 f(x,y)= x*y。这可以写成：((x + y)² — (x² +y²)) / 2

它只使用加法、减法和平方（所有单个输入的函数）。实际的 KART 涉及将减法重新定义为加法（添加负数），但为了简单起见，我在这里跳过了这一点。

KAN（柯尔莫哥洛夫-阿诺德网络）：

与具有固定节点激活函数的传统 MLP（多层感知器）不同，KAN 在边缘上使用可学习的激活函数，本质上是用非线性权重代替线性权重。

这使KAN更加准确并提高了模型可解释性，对于具有系数组合结构的函数更加友好。

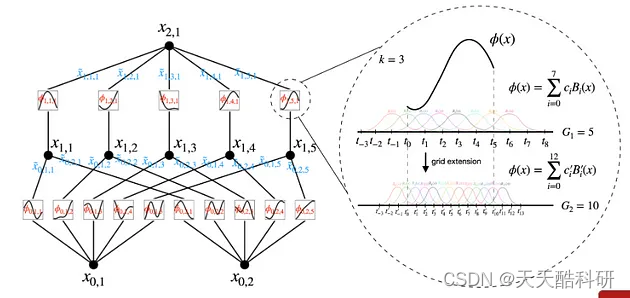
组合结构到底是什么：

当一个函数可以由少量简单函数构建时，它具有稀疏组合结构，每个简单函数仅依赖于几个输入变量。

例如，函数 f(x, y, z) = sin(x) * exp(y) + z 是组合稀疏的，因为࿱