图神经网络入门：GCN论文+源码超级详细注释讲解！_gcn论文源码(pytorch)超级详细注释讲解!

作者：你好赵伟 | 2024-07-16 10:59:19

踩

gcn论文源码(pytorch)超级详细注释讲解!

对GAT源码感兴趣的还可移步：gat源码逐句解读.
对BERT源码感兴趣的还可移步：bert源码（pytorch）逐句解读.

更多论文解读，源码剖析，学习资料，欢迎关注公众号fanNLP

在这里插入图片描述

什么是图神经网络

图神经网络是一种特殊的图表示方法，使用神经网络来对图节点进行编码（encode），将图结构embedding为计算机可处理的向量矩阵。
图网络常常用于：图节点分类，图关系预测，社区发现，网络相似度

详解图神经网络

对于一个图 $G = (V, E)$ , $V$ 代表其顶点集， $E$ 代表其边集，我们需要一个好的编码函数 $E N C$ ，来将这个图编码为向量，这个向量要能尽可能地保留原来的图信息。

我们还需要另外两个函数：

1. $s_G$ 来衡量两个节点之间的相似度。最简单的 $s_G$ 就是两个节点相连就取1，否则为0。也有人通过随机游走来计算两个节点之间的共现概率。

2.编码后对向量相似度进行计算的解码器 $D E C$ 。大部分解码器都是二元的，输入两个节点的编码，返回一个值衡量它们的相似度。

至此，图网络模型学习的目标就为：

设计刻画两个相似度的函数 $s_G$ 与 $D E C$ ，让模型用数据驱动的方式去学习编码器 $E N C$ ，使得两个节点被编码后的相似度 $DEC(ENC(v_1),ENC(v_2))$ 与它们在原始图中的相似度尽可能接近。

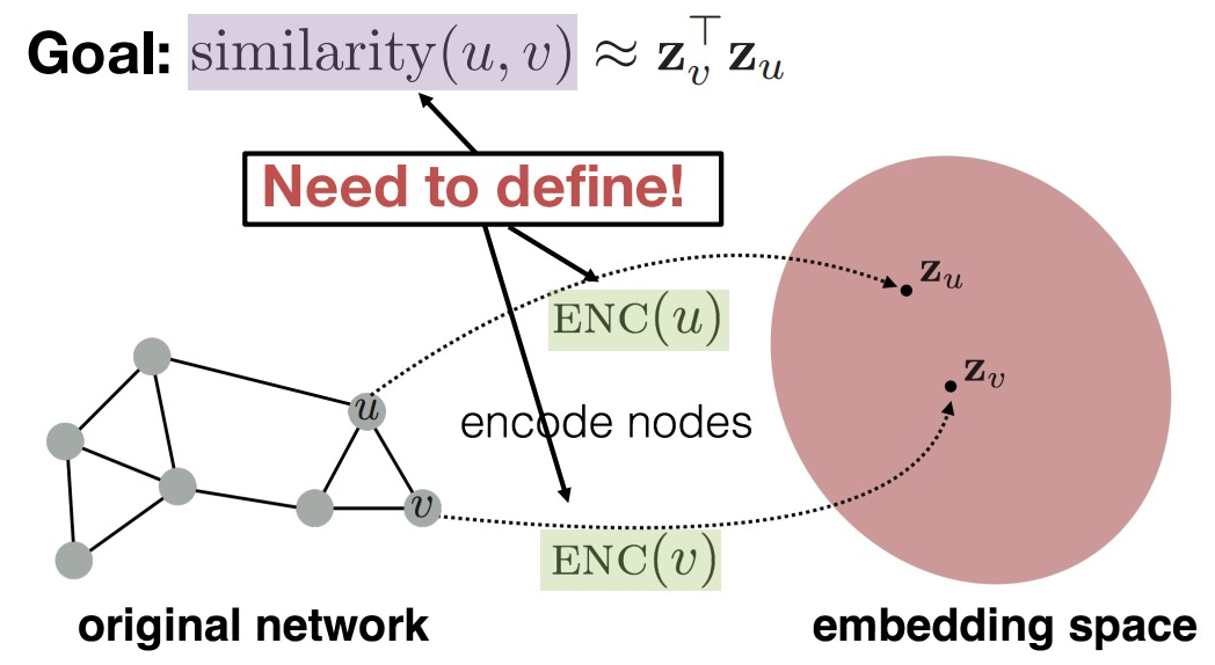
故损失函数就是用来定义图表示中的节点相似度与原图节点中的相似度了。

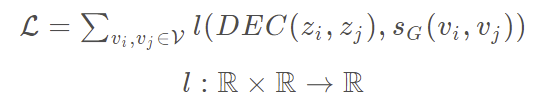
当我们通过训练得到了节点的向量表示，就可以把它们用作下游任务了，比如计算cos相似度衡量两点相似性，节点分类。这里的思想和NLP中的词向量是一致的。

图卷积神经网络

普通图神经网络公式为 $H=\sigma(AXW)$ ,其中A是图的邻接矩阵（NxN大小，如果i和j有连接就是1）， $\sigma$ 是激活函数，W是权重矩阵。

对于GCN，则是做了以下改进：
1.计算时忽略了i节点本身的信息，这时就需要加上对角矩阵 $I$ ，变成 $\hat A= A+I$
2.这个式子计算时只进行了累加，那邻居数多的节点值就会很大，需要用度矩阵(节点邻居个数)归一化，变成 $\hat D^{-1} \hat A$
3.如果i的某个邻居j本身有很多邻居，那j对i的贡献就没那么重要，需要减小权重，但之前已经除以
自己本身的度进行归一化了，这时可以除以两者的几何平均数 $\sqrt{ {\hat D_{ii}} {\hat D_{jj}}}$

最终公式则为：
$Z=f(X,A)=softmax({\hat A} ReLU({\hat A} XW^{(0)})W^{(1)})$

关键点就是通过谱图卷积的方式，获得了临接矩阵A更好的表示，提升效果。

回答几个常问的问题

1.半监督学习是什么？体现在哪里？

参考这篇文章半监督短文本分类的异构图注意网络

2.如何得到每个节点的embedding？
个人理解：model部分，logsoftmax前的x就是每个节点的embedding

def forward(self, x, adj):
    x = F.relu(self.gc1(x, adj))    # adj即公式Z=softmax(A~Relu(A~XW(0))W(1))中的A~
    x = F.dropout(x, self.dropout, training=self.training)  # x要dropout
    x = self.gc2(x, adj)   #embedding
    return F.log_softmax(x, dim=1)
1
2
3
4
5

GCN源码讲解（pytorch）

数据集介绍

cora数据集.

utils.py

import numpy as np
import scipy.sparse as sp
import torch

'''
先将所有由字符串表示的标签数组用set保存，set的重要特征就是元素没有重复，
因此表示成set后可以直接得到所有标签的总数，随后为每个标签分配一个编号，创建一个单位矩阵，
单位矩阵的每一行对应一个one-hot向量，也就是np.identity(len(classes))[i, :]，
再将每个数据对应的标签表示成的one-hot向量，类型为numpy数组
'''
def encode_onehot(labels):
    classes = set(labels)  # set() 函数创建一个无序不重复元素集
    classes_dict = {c: np.identity(len(classes))[i, :] for i, c in  # identity创建方矩阵
                    enumerate(classes)}     # 字典 key为label的值，value为矩阵的每一行
    # enumerate函数用于将一个可遍历的数据对象组合为一个索引序列
    labels_onehot = np.array(list(map(classes_dict.get, labels)),  # get函数得到字典key对应的value
                             dtype=np.int32)
    return labels_onehot
    # map() 会根据提供的函数对指定序列做映射
    # 第一个参数 function 以参数序列中的每一个元素调用 function 函数，返回包含每次 function 函数返回值的新列表
    #  map(lambda x: x ** 2, [1, 2, 3, 4, 5])
    #  output:[1, 4, 9, 16, 25]


def load_data(path="./data/cora/", dataset="cora"):
    """Load citation network dataset (cora only for now)"""
    print('Loading {} dataset...'.format(dataset))

    idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
                                        dtype=np.dtype(str))
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)  # 储存为csr型稀疏矩阵
    labels = encode_onehot(idx_features_labels[:, -1])
    #这里的label为onthot格式，如第一类代表[1,0,0,0,0,0,0]
    # content file的每一行的格式为 ： <paper_id> <word_attributes>+ <class_label>
    #    分别对应 0, 1:-1, -1
    # feature为第二列到倒数第二列，labels为最后一列

    # build graph
    # cites file的每一行格式为：  <cited paper ID>  <citing paper ID>
    # 根据前面的contents与这里的cites创建图，算出edges矩阵与adj 矩阵
    idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
    idx_map = {j: i for i, j in enumerate(idx)}
    # 由于文件中节点并非是按顺序排列的，因此建立一个编号为0-(node_size-1)的哈希表idx_map，
    # 哈希表中每一项为id: number，即节点id对应的编号为number
    edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
                                    dtype=np.int32)
    # edges_unordered为直接从边表文件中直接读取的结果，是一个(edge_num, 2)的数组，每一行表示一条边两个端点的idx
    edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),  # flatten：降维，返回一维数组
                     dtype=np.int32).reshape(edges_unordered.shape)
    # 边的edges_unordered中存储的是端点id，要将每一项的id换成编号。
    # 在idx_map中以idx作为键查找得到对应节点的编号，reshape成与edges_unordered形状一样的数组
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),  # coo型稀疏矩阵
                        shape=(labels.shape[0], labels.shape[0]),
                        dtype=np.float32)
    # 根据coo矩阵性质，这一段的作用就是，网络有多少条边，邻接矩阵就有多少个1，
    # 所以先创建一个长度为edge_num的全1数组，每个1的填充位置就是一条边中两个端点的编号，
    # 即edges[:, 0], edges[:, 1]，矩阵的形状为(node_size, node_size)。


    # build symmetric adjacency matrix   论文里A^=(D~)^0.5 A~ (D~)^0.5这个公式
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
    # 对于无向图，邻接矩阵是对称的。上一步得到的adj是按有向图构建的，转换成无向图的邻接矩阵需要扩充成对称矩阵
    features = normalize(features)
    adj = normalize(adj + sp.eye(adj.shape[0]))   # eye创建单位矩阵，第一个参数为行数，第二个为列数
    # 对应公式A~=A+IN

    # 分别构建训练集、验证集、测试集，并创建特征矩阵、标签向量和邻接矩阵的tensor，用来做模型的输入
    idx_train = range(140)
    idx_val = range(200, 500)
    idx_test = range(500, 1500)

    features = torch.FloatTensor(np.array(features.todense()))  # tensor为pytorch常用的数据结构
    labels = torch.LongTensor(np.where(labels)[1])
    #这里将onthot label转回index
    adj = sparse_mx_to_torch_sparse_tensor(adj)   # 邻接矩阵转为tensor处理

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test

def normalize(mx):
    """Row-normalize sparse matrix"""
    rowsum = np.array(mx.sum(1))  # 对每一行求和
    r_inv = np.power(rowsum, -1).flatten()  # 求倒数
    r_inv[np.isinf(r_inv)] = 0.  # 如果某一行全为0，则r_inv算出来会等于无穷大，将这些行的r_inv置为0
    r_mat_inv = sp.diags(r_inv)  # 构建对角元素为r_inv的对角矩阵
    mx = r_mat_inv.dot(mx)
    # 用对角矩阵与原始矩阵的点积起到标准化的作用，原始矩阵中每一行元素都会与对应的r_inv相乘，最终相当于除以了sum
    return mx

def accuracy(output, labels):
    preds = output.max(1)[1].type_as(labels) # 使用type_as(tesnor)将张量转换为给定类型的张量。
    correct = preds.eq(labels).double()  # 记录等于preds的label eq:equal
    correct = correct.sum()
    return correct / len(labels)


def sparse_mx_to_torch_sparse_tensor(sparse_mx):    # 把一个sparse matrix转为torch稀疏张量
    """
    numpy中的ndarray转化成pytorch中的tensor : torch.from_numpy()
    pytorch中的tensor转化成numpy中的ndarray : numpy()
    """
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    # 不懂的可以去看看COO性稀疏矩阵的结构
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices, values, shape)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

train.py

from __future__ import division
from __future__ import print_function

import time
import argparse  # argparse 是python自带的命令行参数解析包，可以用来方便地读取命令行参数
import numpy as np

import torch
import torch.nn.functional as F
import torch.optim as optim

from pygcn.utils import load_data, accuracy
from pygcn.models import GCN

# Training settings
parser = argparse.ArgumentParser()
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='Disables CUDA training.')
parser.add_argument('--fastmode', action='store_true', default=False,
                    help='Validate during training pass.')
parser.add_argument('--seed', type=int, default=42, help='Random seed.')
parser.add_argument('--epochs', type=int, default=200,
                    help='Number of epochs to train.')
parser.add_argument('--lr', type=float, default=0.01,
                    help='Initial learning rate.')
parser.add_argument('--weight_decay', type=float, default=5e-4,
                    help='Weight decay (L2 loss on parameters).')
parser.add_argument('--hidden', type=int, default=16,
                    help='Number of hidden units.')
parser.add_argument('--dropout', type=float, default=0.5,
                    help='Dropout rate (1 - keep probability).')

# 如果程序不禁止使用gpu且当前主机的gpu可用，arg.cuda就为True
args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()

np.random.seed(args.seed)
torch.manual_seed(args.seed)   # 为CPU设置种子用于生成随机数，以使得结果是确定的
if args.cuda:
    torch.cuda.manual_seed(args.seed)

# Load data
adj, features, labels, idx_train, idx_val, idx_test = load_data()

# Model and optimizer
model = GCN(nfeat=features.shape[1],
            nhid=args.hidden,
            nclass=labels.max().item() + 1,
            dropout=args.dropout)
optimizer = optim.Adam(model.parameters(),
                       lr=args.lr, weight_decay=args.weight_decay)

# 数据写入cuda，便于后续加速
if args.cuda:
    model.cuda()   # . cuda()会分配到显存里（如果gpu可用）
    features = features.cuda()
    adj = adj.cuda()
    labels = labels.cuda()
    idx_train = idx_train.cuda()
    idx_val = idx_val.cuda()
    idx_test = idx_test.cuda()

def train(epoch):
    t = time.time()  # 返回当前时间
    model.train()
    optimizer.zero_grad()
    # optimizer.zero_grad()意思是把梯度置零，也就是把loss关于weight的导数变成0.
    # pytorch中每一轮batch需要设置optimizer.zero_gra
    output = model(features, adj)
    loss_train = F.nll_loss(output[idx_train], labels[idx_train])
    # 由于在算output时已经使用了log_softmax，这里使用的损失函数就是NLLloss，如果前面没有加log运算，
    # 这里就要使用CrossEntropyLoss了
    # 损失函数NLLLoss() 的输入是一个对数概率向量和一个目标标签. 它不会为我们计算对数概率，
    # 适合最后一层是log_softmax()的网络. 损失函数 CrossEntropyLoss() 与 NLLLoss() 类似,
    # 唯一的不同是它为我们去做 softmax.可以理解为：CrossEntropyLoss()=log_softmax() + NLLLoss()
    # https://blog.csdn.net/hao5335156/article/details/80607732
    acc_train = accuracy(output[idx_train], labels[idx_train])  #计算准确率
    loss_train.backward()  # 反向求导  Back Propagation
    optimizer.step()  # 更新所有的参数  Gradient Descent

    if not args.fastmode:
        # Evaluate validation set performance separately,
        # deactivates dropout during validation run.
        model.eval()  # eval() 函数用来执行一个字符串表达式，并返回表达式的值
        output = model(features, adj)

    loss_val = F.nll_loss(output[idx_val], labels[idx_val])    # 验证集的损失函数
    acc_val = accuracy(output[idx_val], labels[idx_val])
    print('Epoch: {:04d}'.format(epoch+1),
          'loss_train: {:.4f}'.format(loss_train.item()),
          'acc_train: {:.4f}'.format(acc_train.item()),
          'loss_val: {:.4f}'.format(loss_val.item()),
          'acc_val: {:.4f}'.format(acc_val.item()),
          'time: {:.4f}s'.format(time.time() - t))

# 定义测试函数，相当于对已有的模型在测试集上运行对应的loss与accuracy
def test():
    model.eval()
    output = model(features, adj)
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    print("Test set results:",
          "loss= {:.4f}".format(loss_test.item()),
          "accuracy= {:.4f}".format(acc_test.item()))


# Train model  逐个epoch进行train，最后test
t_total = time.time()
for epoch in range(args.epochs):
    train(epoch)
print("Optimization Finished!")
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))

test()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115

layer.py

import math

import torch

from torch.nn.parameter import Parameter
from torch.nn.modules.module import Module


class GraphConvolution(Module):

    # 初始化层：输入feature，输出feature，权重，偏移
    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))  # FloatTensor建立tensor
        # 常见用法self.v = torch.nn.Parameter(torch.FloatTensor(hidden_size))：
        # 首先可以把这个函数理解为类型转换函数，将一个不可训练的类型Tensor转换成可以训练的类型parameter并将这个parameter
        # 绑定到这个module里面，所以经过类型转换这个self.v变成了模型的一部分，成为了模型中根据训练可以改动的参数了。
        # 使用这个函数的目的也是想让某些变量在学习的过程中不断的修改其值以达到最优化。
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias', None)
            # Parameters与register_parameter都会向parameters写入参数，但是后者可以支持字符串命名
        self.reset_parameters()

    # 初始化权重
    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        # size()函数主要是用来统计矩阵元素个数，或矩阵某一维上的元素个数的函数  size（1）为行
        self.weight.data.uniform_(-stdv, stdv)  # uniform() 方法将随机生成下一个实数，它在 [x, y] 范围内
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

    '''
    前馈运算 即计算A~ X W(0)
    input X与权重W相乘，然后adj矩阵与他们的积稀疏乘
    直接输入与权重之间进行torch.mm操作，得到support，即XW
    support与adj进行torch.spmm操作，得到output，即AXW选择是否加bias
    '''
    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        # torch.mm(a, b)是矩阵a和b矩阵相乘，torch.mul(a, b)是矩阵a和b对应位相乘，a和b的维度必须相等
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else:
            return output
#通过设置断点，可以看出output的形式是0.01，0.01，0.01，0.01，0.01，#0.01，0.94]，里面的值代表该x对应标签不同的概率，故此值可转换为#[0,0,0,0,0,0,1]，对应我们之前把标签onthot后的第七种标签

    def __repr__(self):
        return self.__class__.__name__ + ' (' \
               + str(self.in_features) + ' -> ' \
               + str(self.out_features) + ')'

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

model.py

import torch.nn as nn
import torch.nn.functional as F
from pygcn.layers import GraphConvolution


class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):  # 底层节点的参数，feature的个数；隐层节点个数；最终的分类数
        super(GCN, self).__init__()  #  super()._init_()在利用父类里的对象构造函数

        self.gc1 = GraphConvolution(nfeat, nhid)   # gc1输入尺寸nfeat，输出尺寸nhid
        self.gc2 = GraphConvolution(nhid, nclass)  # gc2输入尺寸nhid，输出尺寸ncalss
        self.dropout = dropout

    # 输入分别是特征和邻接矩阵。最后输出为输出层做log_softmax变换的结果
    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))    # adj即公式Z=softmax(A~Relu(A~XW(0))W(1))中的A~
        x = F.dropout(x, self.dropout, training=self.training)  # x要dropout
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

参考：

https://blog.csdn.net/weixin_36474809/article/details/89379727
公众号：李rumor

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/你好赵伟/article/detail/833735