热门标签
热门文章
- 1给BERT补充其他特征的编码器实践_bert 自编码器
- 2Cobaltstrike简介及实战_cobalstrike
- 3【数据结构与算法】哈希—— 位图 | 布隆过滤器 | 哈希切割_布隆过滤器 哈希算法
- 4【MySQL】insert和select单表查询详解(包含大量示例,看了必会)_insert select
- 5python控制windows窗口,python 控制桌面程序_pyautoit
- 6QML动画(基本动画)_qml鼠标点击动画
- 7小白如何编写微信小程序的页面结构_小程序页面js的结构设计
- 8深入理解LinkedList_linkedlist 左右哪边是头
- 9使用 FastAPI 实现聊天完成 API 详解_fastapi stream api
- 10sql优化-单表优化_单表慢sql优化
当前位置: article > 正文
利用Python实现纬度加权平均(即NCL中的wgt_areaave)_温度的纬度加权
作者:你好赵伟 | 2024-07-20 11:46:46
赞
踩
温度的纬度加权
当处理全球数据的时候,最常见的分析就是全球、北半球平均了,这时候一定要注意要根据纬度等信息进行加权,求加权平均,要不然结果肯定会不准。
对于NCL中,有现成的函数实现:wgt_areaave
但是对于Python中,常规的计算包里面是没有的,或许现在有其他包可以实现,也可以告诉我~。于是基于numpy写了下面的函数:
- def AreaWeightMean(data2D, lat, lon):
- '''
- data2D: 要进行区域加权平均的变量 2D: [lat, lon]
- lat: data2D对应的纬度 1D 最好不要包括-90° 和 90° 因为NCL 和 Python 计算 np.cos(90 * rad) 值差的很大
- lon: data2D对应的经度 1D
- '''
- jlat = lat.shape[0]
- rad = 4.0 * np.arctan(1.0) / 180.0
- re = 6371220.0
- rr = re * rad
- dlon = np.abs(lon[2] - lon[1]) * rr
- dx = dlon * np.cos(lat * rad)
- dy = np.zeros(jlat)
- dy[0] = np.abs(lat[2] - lat[1]) * rr
- dy[1: jlat - 1] = np.abs(lat[2: jlat]-lat[0: jlat - 2])*rr * 0.5
- dy[jlat - 1] = abs(lat[jlat - 1] - lat[jlat - 2]) * rr
- area = dx * dy
- # dataAreaWeightMean = np.sum(np.dot(area, data2D))/np.sum(area)
- sumtop = 0
- sumbottom = 0
- for id1 in range(data2D.shape[0]):
- for id2 in range(data2D.shape[1]):
- sumtop = sumtop + data2D[id1, id2]*area[id1]
- sumbottom = sumbottom +area[id1]
- dataAreaWeightMean = sumtop/sumbottom
- return dataAreaWeightMean
 '运行
'运行看一下结果对比吧:
直接不加权平均(np.mean(data3D, axis = (1,2)))得到的结果:
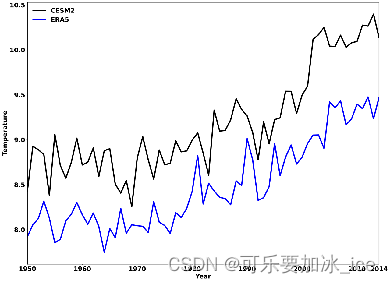
加权平均之后的:
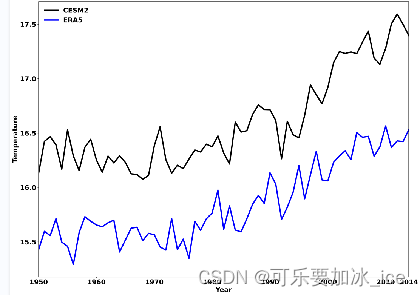
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/你好赵伟/article/detail/856726
推荐阅读
相关标签


