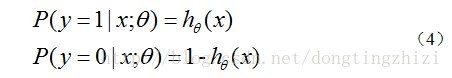逻辑回归原理简述及代码实现_逻辑回归原理及代码实现 csdn

1 逻辑回归原理

逻辑回归与线性回归本质上来说是类似，相较线性回归来说只是多了一个Logistic函数（或称为Sigmoid函数）。

1.1 线性回归

机器学习最通俗的解释就是让机器学会决策。对于我们人来说，比如去菜市场里挑选芒果，从一堆芒果中拿出一个，根据果皮颜色、大小、软硬等属性或叫做特征，我们就会知道它甜还是不甜。类似的，机器学习就是把这些属性信息量化后输入计算机模型，从而让机器自动判断一个芒果是甜是酸，这实际上就是一个分类问题。

分类和回归是机器学习可以解决两大主要问题，从预测值的类型上看，连续变量预测的定量输出称为回归；离散变量预测的定性输出称为分类。例如：预测明天多少度，是一个回归任务；预测明天阴、晴、雨，就是一个分类任务。

1.2 逻辑回归

Logistic Regression原理与Linear Regression回归类似，其主要流程分为：
（1）构建预测函数。一般来说在构建之前，需要根据数据来确定函数模型，是线性还是非线性。
（2）构建Cost函数(损失函数)。该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差。
（3）采用梯度下降算法，minJ(θ)。在数据量很大时，梯度下降算法执行起来会较慢。因此出现了随机梯度下降等算法进行优化。

2 具体过程

2.1 构造预测函数

在线性回归中模型中预测函数为：

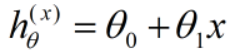
逻辑回归作为分类问题，结果h = {1 or 0}即可。若逻辑回归采用线性回归预测函数则会产生远大于1或远小于0得值，不便于预测。因此线性回归预测函数需要做一定改进。设想如果有一个函数h(x)能够把预测结果值压缩到0-1这个区间，那么我们就可以设定一个阈值s，若h(x) >= s,则认定为预测结果为1，否之为0。
实际中也存在这样函数：Logistic函数（或称为Sigmoid函数），函数表达式为：


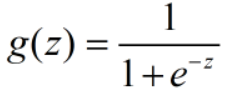
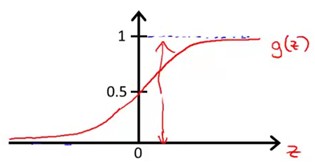
从上图可以看到，g(z)随着z不断增大越来越靠近1但不会超过1，相反随着z不断减少越来越靠近0但不会小于0。此类函数完美满足前面线性函数作为逻辑回归函数模型中得不足。因此集合Sigmoid函数就可以构造预测函数。
接下来需要确定数据划分的边界类型，对于图1和图2中的两种数据分布，显然图1需要一个线性的边界，而图2需要一个非线性的边界。接下来我们只讨论线性边界的情况。
在构建预测函数时，首先通过数据得到大概得决策边界。例图1中的边界为线性边界。本文也只分析线性边界。

经过公式1与公式2整合，得到公式3，即逻辑回归预测函数。hθ(x)函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

2.2 构造损失函数J(θ）

损失函数J(θ）是由极大似然法推导而来，本文暂时不给出公式推导，直接借用吴恩达老师课中给出的损失函数J(θ)。

对上述公式进行整合可以得到如下公式：
上述公式则为逻辑回归的损失函数J(θ)，接下则需要通过训练减少J(θ)。

2.3 采用梯度下降算法minJ(θ)

求J(θ)可以通过最小值可以通过梯度下降算法，根据梯度下降算法可以得到θ不断更新的过程。

定义一个f(x),f(x)原型和求导如下。

对θ更新会用到上式公式，读者可以自己推导一下。
求偏导如下：

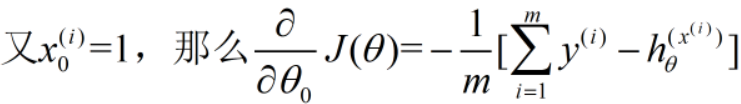
2.4 采用向量化进行优化

对θ更新时，需要多层循环嵌套取得一些值，对此用向量化来进行优化。
假设有m个样本，每个样本有n+1个特征，θ0 = 1，则就可以构建一个mx(n+1)的样例矩阵。

特征值向量

对A矩阵经过sigmod函数处理，得到预测函数h和误差矩阵。

通过构建此类矩阵，并按照一定的运算规则，会加快梯度下降速度。α为学习步长。

同理对其它θ参数更新时规则如下：
与其像上面逐步分开求θ参数变化，可以将θ整合到一块处理更快速。
以上是向量化全部介绍。通过向量化不仅可以减少出错，还可以提高效率，建议多使用向量化来进行编程，解决实际问题。

3 python实现逻辑回归

import numpy as np
import matplotlib.pyplot as plt

class LogisticReg():

    def __init__(self):
        pass

    def sigmod(self,x):
        return 1.0/(1+np.exp(-x))
    
    def get_data(self,path):

        self.x = []
        self.y = []
        dat = open(path)

        for line in dat:
            temp = line.split()
            self.x.append(temp[:2])
            self.y.append(temp[2])
        self.y = list(map(lambda x:float(x),self.y))
        self.y = np.array(self.y)
        self.y = self.y.reshape((len(self.y, )))
        self.x = np.array(self.x)
        self.x = self.x.reshape((len(self.x), len(self.x[0])))
        self.x = self.stringTofloat(self.x)
        # print(self.x,self.y)

    def init_data(self,path):
        data = np.loadtxt(path)
        # print(data)
        dataMatIn = data[:,0:-1]
        dataLabel = data[:,-1:]
        dataMatIn = np.insert(dataMatIn,0,1,axis = 1)
        return dataMatIn,dataLabel

    def stringTofloat(self,number):

        # number is Two-dimensional array
        (m,n) = number.shape
        x = np.zeros((m,n))
        for i in range(m):
            for j in range(n):
                # print(float(number[i,j]))
                x[i][j] = float(number[i][j])
        return x

    def LogisticRegGradinet(self,theta,learing_rate,dataMatIn,dataLabel):
        m = dataMatIn.shape[0]
        dataMatIn = np.mat(dataMatIn)
        dataLabel = np.mat(dataLabel)
        h = self.sigmod(dataMatIn*theta)
        err = h-dataLabel
        weights = theta.copy()
        weights = weights - learing_rate*1.0/m*dataMatIn.transpose()*err
        return weights

    def trainLogisticRegression(self,interations,learing_rate,dataMatIn,dataLabel):
        theta = np.ones((dataMatIn.shape[1],1))
        for i in range(interations):
            theta = self.LogisticRegGradinet(theta,learing_rate,dataMatIn,dataLabel)
        return theta

    def plotBestFIt(self,dataMatIn,dataLabel,weights):
        self.x = dataMatIn.reshape((dataMatIn.shape[0],dataMatIn.shape[1]))
        self.y = dataLabel.reshape((dataLabel.shape[0],))
        m = dataMatIn.shape[0]
        print(weights.shape,weights[0][0],weights[1][0],weights[2][0])
        xcord1 = []
        ycord1 = []
        xcord2 = []
        ycord2 = []
        for i in range(m):
            if self.y[i] == 1:
                xcord1.append(self.x[i][1])
                ycord1.append(self.x[i][2])
            else:
                xcord2.append(self.x[i][1])
                ycord2.append(self.x[i][2])
        fig = plt.figure()
        ax = fig.add_subplot(111)
        ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
        ax.scatter(xcord2, ycord2, s=30, c='green')
        x = np.arange(-3, 3, 0.1)
        y = (-float(weights[0][0]) - (float(weights[1][0]) * x)) / float(weights[2][0])  # matix
        ax.plot(x, y)
        plt.xlabel('X1')
        plt.ylabel('X2')
        plt.show()

    def run(self):

        path = "D:\\Data\\LogisticReg\\data.txt"
        dataMatIn,dataLabel = self.init_data(path)
        interations = 5000 #最大迭代次数
        learing_rate = 0.01 #学习步长
        theta = self.trainLogisticRegression(interations,learing_rate,dataMatIn,dataLabel)
        self.plotBestFIt(dataMatIn,dataLabel,theta)

    def test(self):
        self.init_data("D:\\Data\\LogisticReg\\data.txt")


if __name__ == "__main__":

    f = LogisticReg()
    f.run()
    # f.test()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109

参考文章
机器学习之逻辑回归(纯python实现)
逻辑回归（Logistic Regression, LR）简介