- 1git常用命令总结_git查看公钥命令
- 2基于WSL2+Docker+VScode搭建机器学习(深度学习)开发环境_wsl docker
- 3C语言strcpy函数实现_strcpy实现
- 4python3.8使用aiml总结_alice_path
- 5中文语音克隆|MockingBird(拟声鸟)github项目运行流程(一次跑通)_拟声鸟工具箱
- 6【论文投稿】计算机学科部分核心期刊投稿攻略_计算机系统应用稿费一般多少
- 7新建SQL Server用户并授予查询,插入权限_sqlserver命令添加新用户并授予所有权限
- 8axure管理系统原型模板_PRD分享:B端产品需求文档怎么写? (附案例文档+原型)...
- 9手把手带你学习如何在小程序、网页前端部署AI模型
- 10网易互娱游戏测试岗位面试喜欢问什么?_大批量测试伤害输出怎么测试
上下文无关文法和语言_c语言是上下文无关文法吗
赞
踩
1.文法及语言的形式表示
每一门编程语法都是有它自己的语法的,实际上,任何程序均可以看做是一定字符集上的一个字符串,而判定一个字符串是否为一个程序上合法的程序,其依据的则是语言的文法。
语言的文法是一组规则,包含词法规则和语法规则。
词法规则是描述语言单词符号构成规则的。单词符号包括:关键字、标识符(变量名或函数名等)、常数、运算符等。词法规则的描述工具通常为正规文法(正规式、有限自动机)。
语法规则是描述语言语法单位构成规则的。语法单位包括:表达式、语句、函数、过程等。语法规则的描述工具常为:上下文无关文法。
文法是描述语言结构的形式规则,一般分为四个类型:0型、1型、2型、3型。其中2型即为上下文无关文法,是描述程序语言语法的有效工具,3型即正规文法,是描述程序语言词法的有效工具。
(最常见的文法的分类系统是诺姆·乔姆斯基于1956年发展的乔姆斯基谱系,这个分类谱系把所有的文法分成四种类型:无限制文法、上下文相关文法、上下文无关文法和正规文法。四类文法对应的语言类分别是递归可枚举语言、上下文相关语言、上下文无关语言和正规语言。)
2.文法和语言的形式定义
定义1:产生式(或规则)
产生式是一个有序对(A,α),通常记作A→α(或A::=α),其中A称为产生式的左部符号,α为产生式的右部有穷符号串,“→”表示“定义为”或“由…组成”。
定义2:文法
文法是一个四元组G[S]=(Vn,Vt,P,S),其中Vn为非空有穷集,其每个元素为非终结符,Vt为非空有穷集,其每个元素为终结符,由定义可知Vn∩Vt=Φ,文法符号集V=Vn∪Vt,P为产生式的有穷集合,每个产生式的形式为:A→α,A∈Vn,α∈V*,S为文法的开始符号S∈Vn。
Vn:非空有限的非终结符集合
Vt:非空有限的终结符集
S:开始符号
P:产生式集合
其中,Vn∩Vt=∅,S∈Vn
P中产生式一般形式为A→α|β,其中A∈Vn,α,β∈(Vn∪Vt)*
定义3:推导与归约
设G[S]=(Vn,Vt,P,S)是给定文法,x,y,A,β∈V*,且A→β∈P,此时符号串xAy能够直接产生出符号串xβy,我们称符号串xβy是符号串xAy的直接推导,或符号串xAy是符号串xβy的直接归约,记作xAy⇒xβy。
定义4:句型和句子
设G[S]=(Vn,Vt,P,S)是给定文法
若S⇒α,α∈V,则称α为文法G的句型。
若S⇒+α,α∈Vt*,则称α为文法G的句子。
例如:<无符号整数>、<数字串>、<数字串><数字>、<数字><数字>、5<数字>、56等均为文法的句型。而7、78、98、1212、32343、均为文法的句子。
定义5:语言
文法G[S]产生的所有句子的集合,称为文法G[S]所定义的语言,记为L(G[S]),即L(G[S])={w|w∈Vt*,且S⇒*w}。

例如:
求此文法所产生的语言。
通过产生式P我们可以知道,此文法产生的语言是:以终结符a1,a2,…an为运算对象,以∧∨ ~为运算符,以[ , ]为分隔符的布尔表达式串。
定义6:规范推导与规范规约
对于直接推导xAy⇒xβy,如y为Vt串或空符号串,则这种推导就称为规范推导(最右推导);与其对应的规约称为规范规约(最左规约)
例如:规范推导过程
<无符号整数>⇒<数字串>
⇒<数字串><数字>
⇒<数字串>6
⇒<数字>6
⇒66
同时,规范推导所得到的句型称为规范句型(最右句型)
形式语言理论的两个结论
(1)给定一个文法G,就能从结构上唯一的确定其语言,即G→L(G)
(2)给定语言L(G),可确定其文法,但其文法不是唯一的。即L→G1或G2…
定义7:等价文法
G1和G2是两个不同的文法如果L(G1)=L(G2),则称G1和G2 为等价文法。
定义8:递归产生式和递归文法
(1)递归产生式:对于文法G=(Vn,Vt,P,S),若A→α∈P,且有α⇒*xAy,则称产生式A→α是递归产生式。
(2)递归文法:含有递归产生式的文法称为递归文法,递归文法定义的语言集L(G)是无穷的,即递归文法可用有穷的产生式来描述无穷的语言。
定义9:短语、直接短语和句柄
设G[S]=(Vn,Vt,P,S)是给定文法,U∈Vn,x,y,u∈V*,
(1)若有S⇒*xUy⇒+xuy,则称u是句型xuy相对于非终结符号U的短语,特别的若有S⇒*xUy⇒xuy,则称u是句型xuy相对于U的直接短语。其中*表示零步以上推导,+表示一步以上推导。
(2)句型的最左直接短语称为该句型的句柄。
例如:
<无符号整数>⇒<数字串>
⇒<数字串><数字>
⇒<数字串>6
⇒<数字>6
⇒66
6 是句型 <数字>6 相对于 <数字> 的短语
<数字>6 是句型 <数字>6 相对于 <数字串> 的短语
<数字> 是句型 <数字>6 相对于 <数字串> 的直接短语,并且是句柄
定义10:文法的二义性
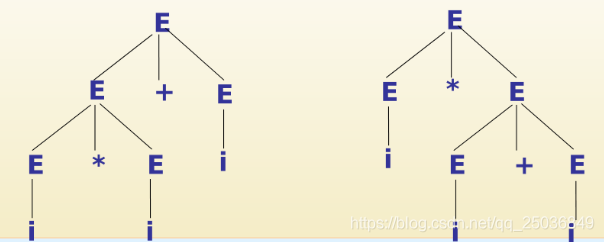
若文法中存在一个句子对应两棵不同的语法树,则称此文发为二义性文法。
例如:文法G[E]的产生式集合如下:E→ E + E | E * E | (E) | i
其句子i * i + i 的语法树有如下两棵
综合训练

解:(1)aacb是G[S]中的句子。
最左推导如下:
S⇒aAcB
⇒aacB (由A→a推导出)
⇒aacb (由B→b推导出)
最右推导如下:
S⇒aAcB
⇒aAcb (由B→b推导出)
⇒aacb (由A→a推导出)
语法树如下:
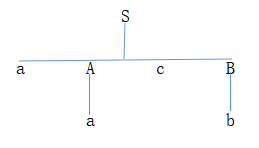
直接短语如下:
a是句型aacb相对于A的句柄;
b是句型aacb相对于aAcB的短语
b是句型aAcb相对于aAcB的直接短语


