回溯法——利用解空间树解决0-1背包问题_回溯法求解01背包约束条件

一、简介

01背包典型的解法是动态规划，之前的博客也有介绍，这里就不再赘述。

https://blog.csdn.net/Jayphone17/article/details/102553763

这里有一些回溯法相关的基础理论知识：

https://blog.csdn.net/Jayphone17/article/details/102910824

二、算法设计

（1）定义问题解空间

购物车问题属于典型的01背包问题，问题的解是从n个物品中选择一些物品使其在不超过容量的前提下价值最大。没个物品有且仅有两种状态，要么装进购物车，要么不装进。用0表示不装进购物车，用1表示装进购物车。所以该问题的解是一个n元组，且每个分量的取值为0或者1。

（2）确定解空间组织结构

问题的解空间描述了2^n种可能接，也可以说是n个元素组成的集合所有子集个数。

可见，问题的解空间树为自己输，且是二叉树，解空间树的深度为问题的规模n。如图所示：

（3）搜索解空间树

1.约束条件：

购物车问题的解空间包含2^n种可能解，存在某种或某些物品无法装进购物车的情况，因此需要设置约束条件，判断装进购物车的物品总重量是否超过购物车的重量，如果超出，就是不可行解，否则为可行解。搜索过程不再搜索那些导致不可行解的结点及其孩子结点。

约束条件是：

2.限界条件：

购物车01背包问题的可行解可能不止一个，问题的目标是找一个装入购物车的物品总结之最大的可行解，即最优解。因此，需要设置衔接条件来加速找出该最优解的速度。

根据解空间树的组织结构，对于任何一个中间结点z（中间状态），从根结点到z结点的分支所代表的状态（是否已经装进购物车）已经确定，从z到其子孙结点的分支状态是不确定的。

也就是说，如果z在解空间树中所处的层次是t，说明第一个物品到t-1个物品的状态已经是确定了。我们只需要沿着z的分支扩展很容易确定第t种物品的状态。此时，1～t种物品的状态已经确定了。

但是t+1～n种物品的状态还不确定。

我们设置前t种物品的状态是已经装进购物车的物品的总价值，用cp表示。

我们设置t+1～n种物品总价值用rp表示。

因此我们用cp+rp是所有从根结点出发经过中间结点z的可行解的价值上界。

• 如果价值上界小于或者等于当前搜索到的最优值（用bestp表示，初始值为0），则说明从中间结点z继续向子孙结点搜索不可能得到一个更优解，没有搜索的必要（剪枝），反之，继续向子孙结点搜索。
• 限界条件为：cp+rp<=bestp 

3.搜索过程：

从根结点开始，以深度优先搜索（DFS）的方式进行搜索。根结点成为活结点，也是当前的扩展结点。

我们约定子树集左分支的值是1，因此沿着扩展结点的左分支进行扩展，代表装进购物车。

在此时需要判断 约束条件 是否成立

• 如果成立，则扩展当前结点生成左子树，继续进行深度优秀搜索，如此往复。
• 如果不成立，剪掉扩展结点的左分支，对右分支进行扩展，代表不装进购物车。在此时，沿着右子树也可能生成最优解，所以我们这时候要判断 限界条件 ，如果满足，则说明有可能生成最优解，此时右结点成为活结点，继续扩展。
• 如果不满足 限界条件 剪掉扩展的右边分支，向最近的 父结点 回溯。
• 直到死结点。

 

三、详细过程

假设现在有4个物品还有1台容量是10的购物车，每个物品的重量是：w（2，5，4，2），价值是v（6，3，5，4）。

（1）初始化。

设置sumw和sumv分别用来统计所有物品的总重量还有总价值。

sumw=13，sumv=18，sumw>10，说明不可以全部装完，需要搜索求解。

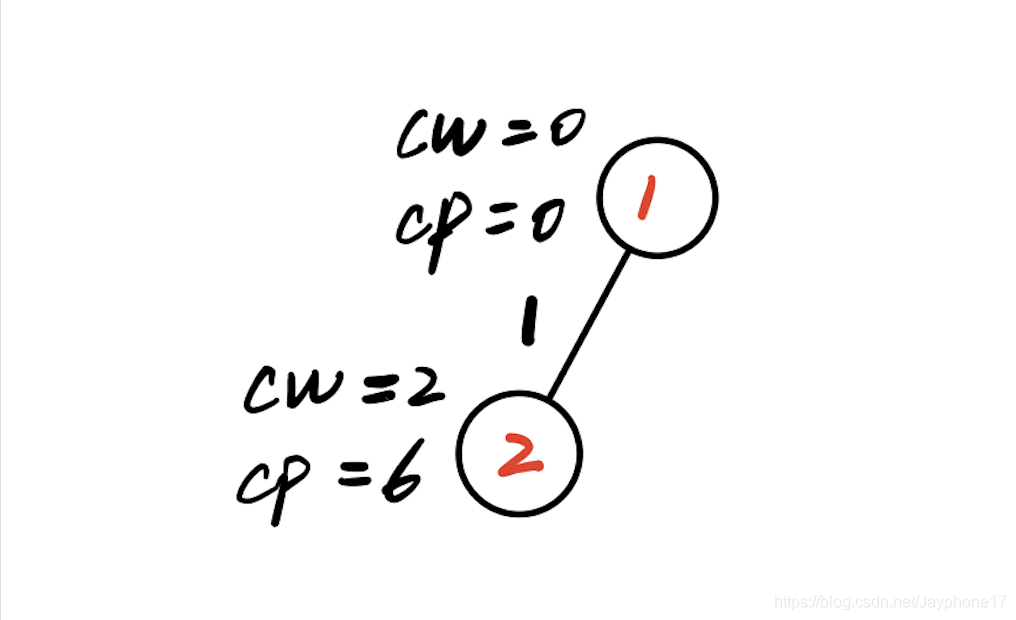
初始化放进购物车的总重量cw=0。当前放进购物车物品总价值cp=0。最优值bestp=0。

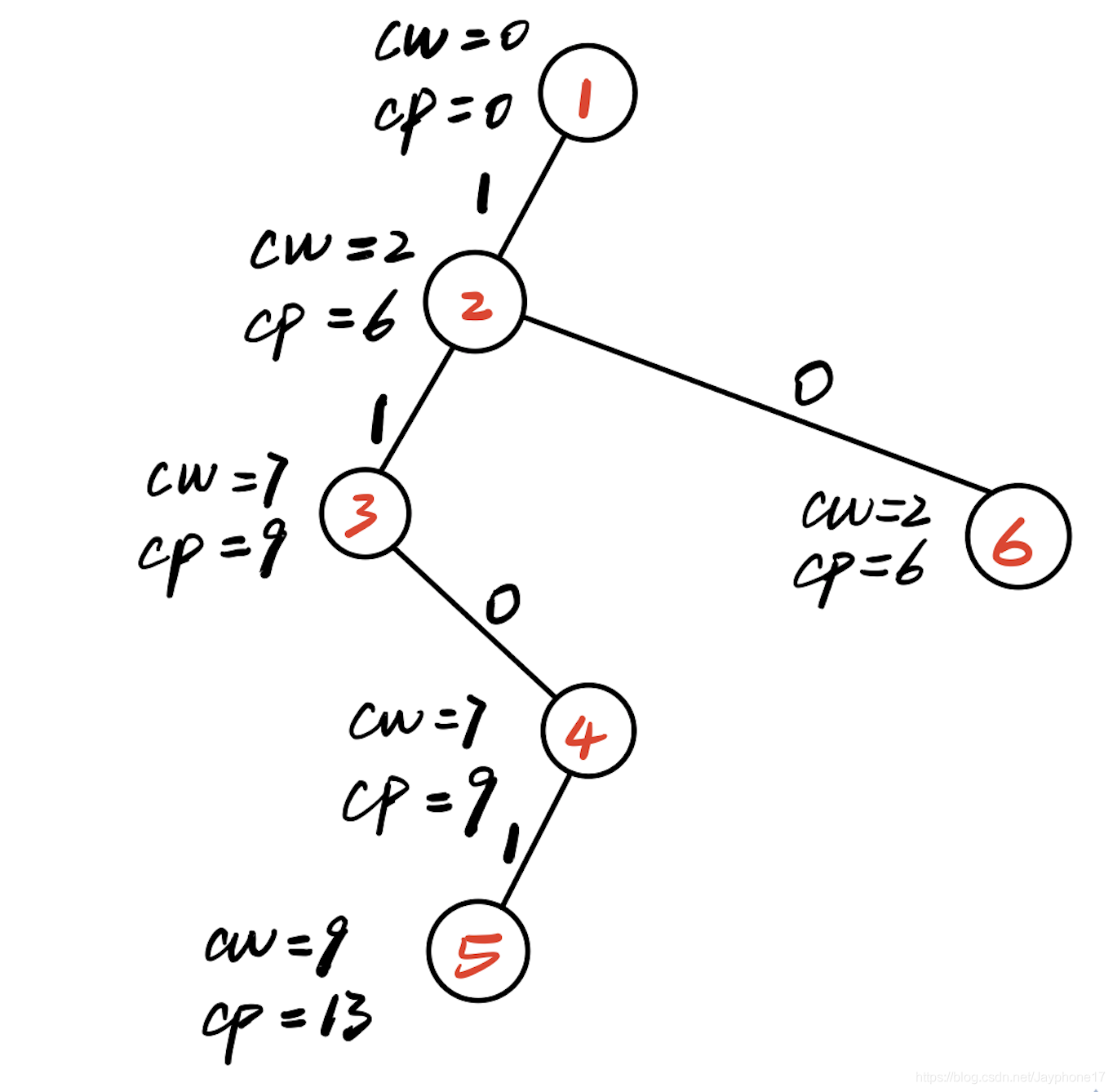
（2）扩展根结点，生成二号结点（第一层）

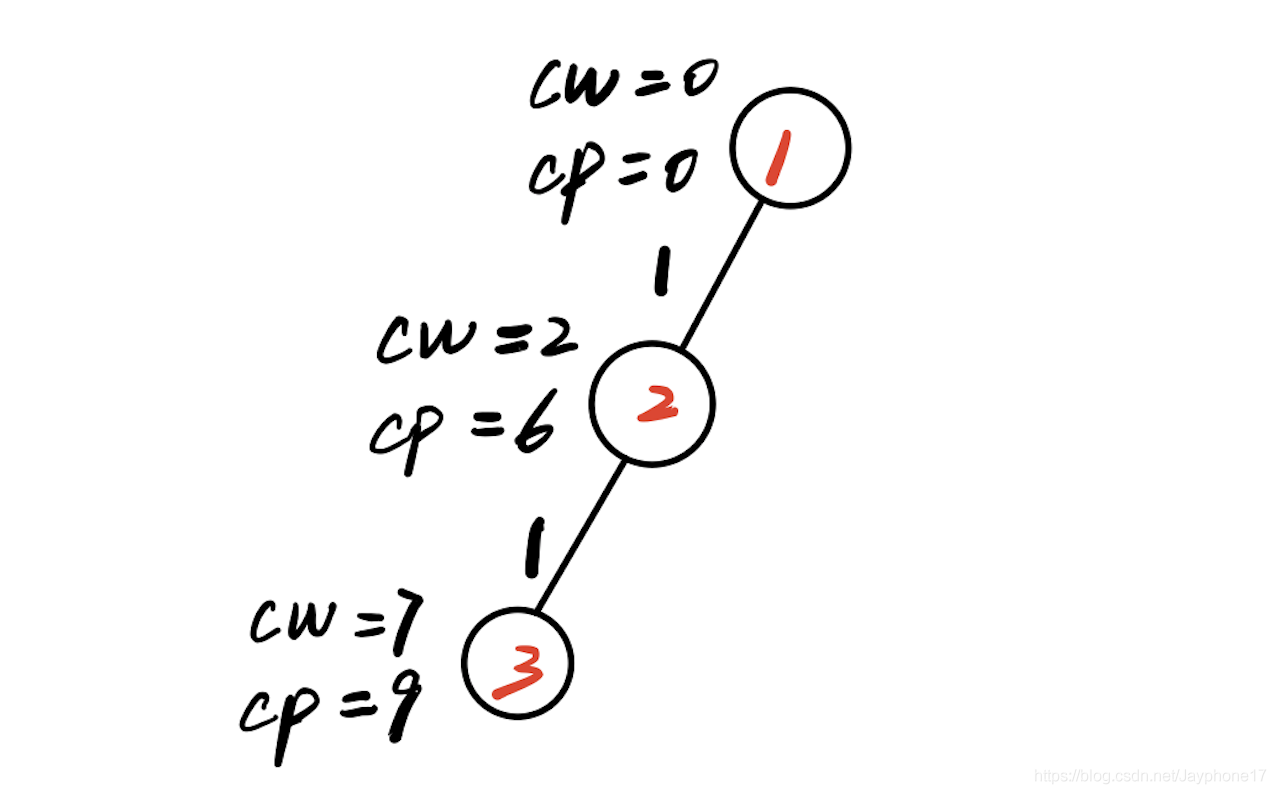
（3）此时重量cw<10，继续扩展二号结点（第二层）

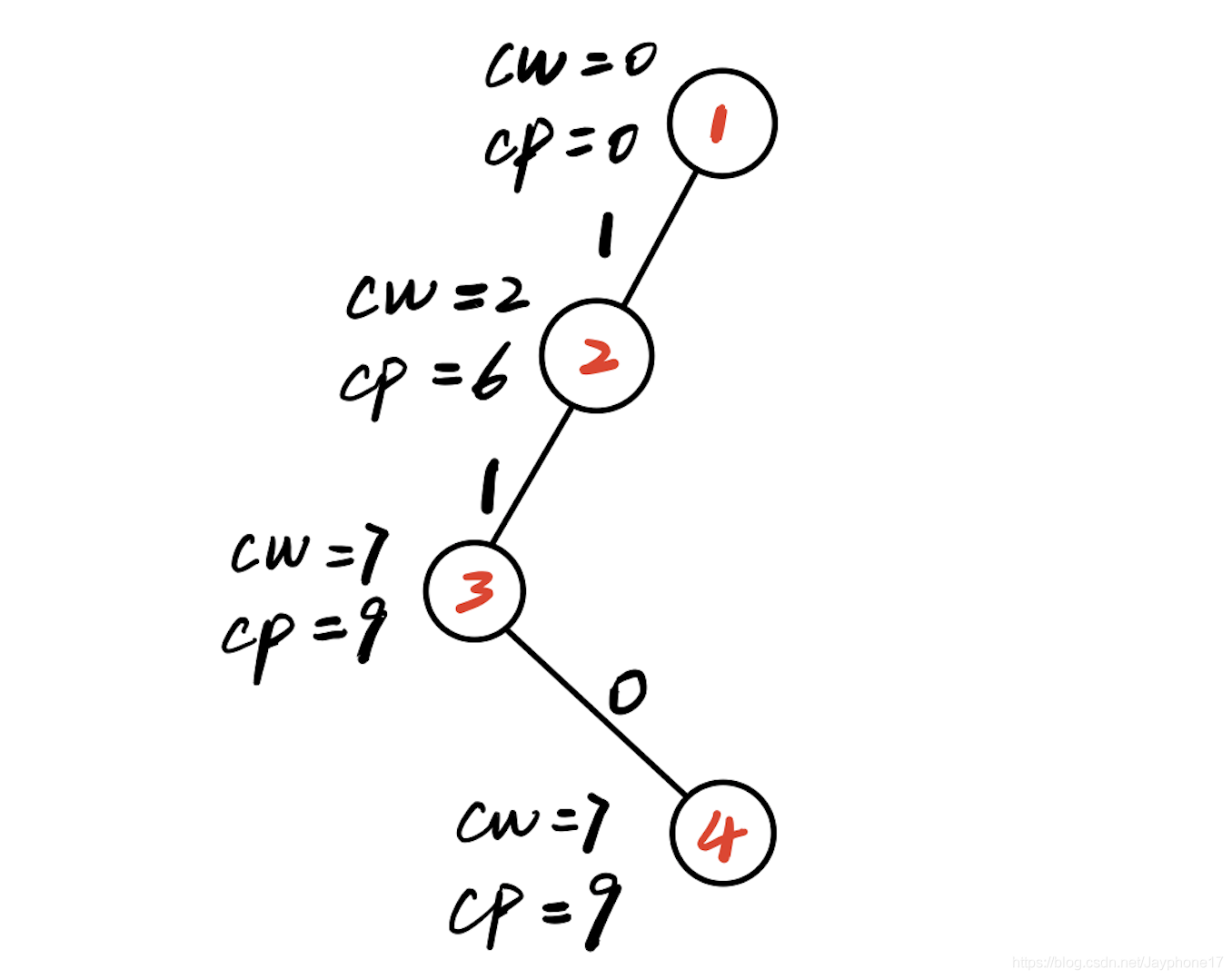
（4）此时cw+w[3]=11>W=10，说明第三个物品不能犯禁，那么判断cw+cp是否大于bestp，此时rp=4，cp+rp=13，bestp=0，因此满足限界条件，扩展右子树，生成4号结点（第三层）

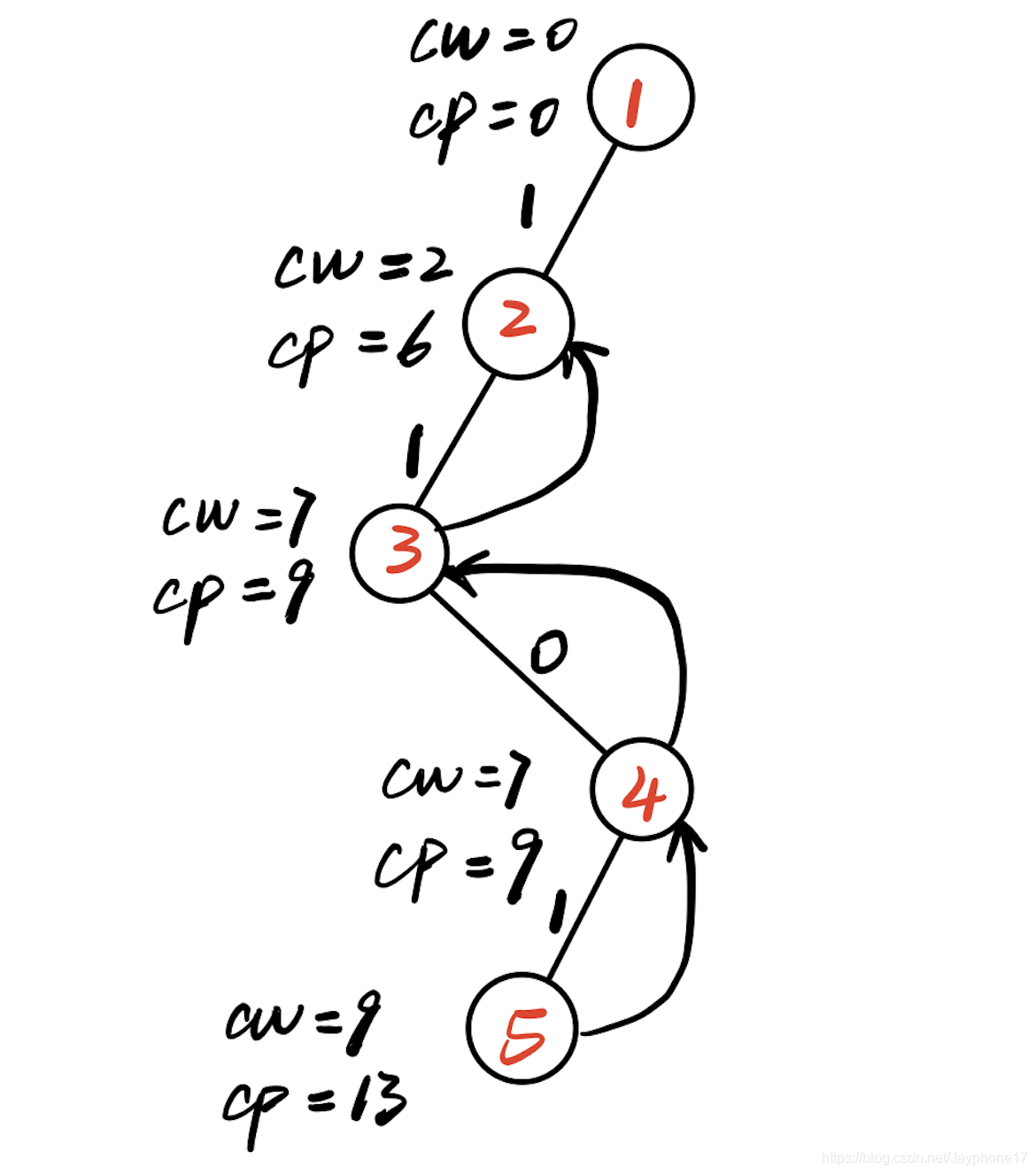
（5）扩展4号结点，首先判断cw+w[4]=9<10=W，满足约束条件，扩展左分支，生成5号结点（第四层）

（6）此时5号结点的深度是5>n=物品的个数，此时找到一个最优解，更新最优解的值bestp=13。此时5号结点已经成为死结点。搜索结束，开始回溯。

（7）回溯到4号结点，此时没有剩余物品，rp=0，cp=9，cp+rp=9<13，因此不扩展右边结点，剪枝，所以4号结点成为死结点。

（8）回溯到3号结点，3号结点的左分支已经剪枝，所以3结点也成为死结点。

（9）回溯到2号结点，此时剩余物品有两个，rp=9，cp=6，cp+rp=15>13=bestp，故扩展右分支，生成6号结点。

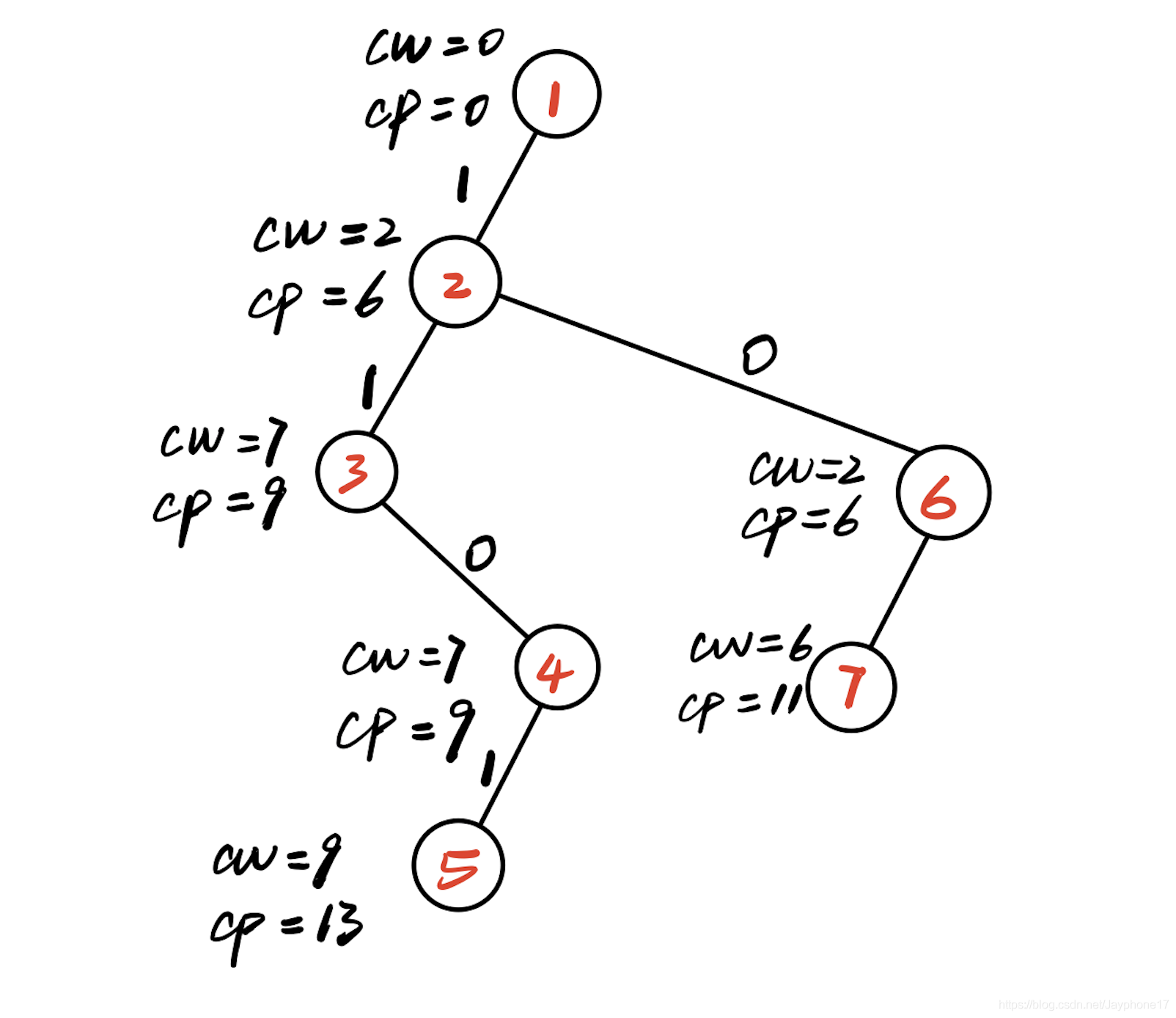
（10）判断6号结点，cw+w[3]=6<W，满足约束条件，扩展左分支，生成7号结点。

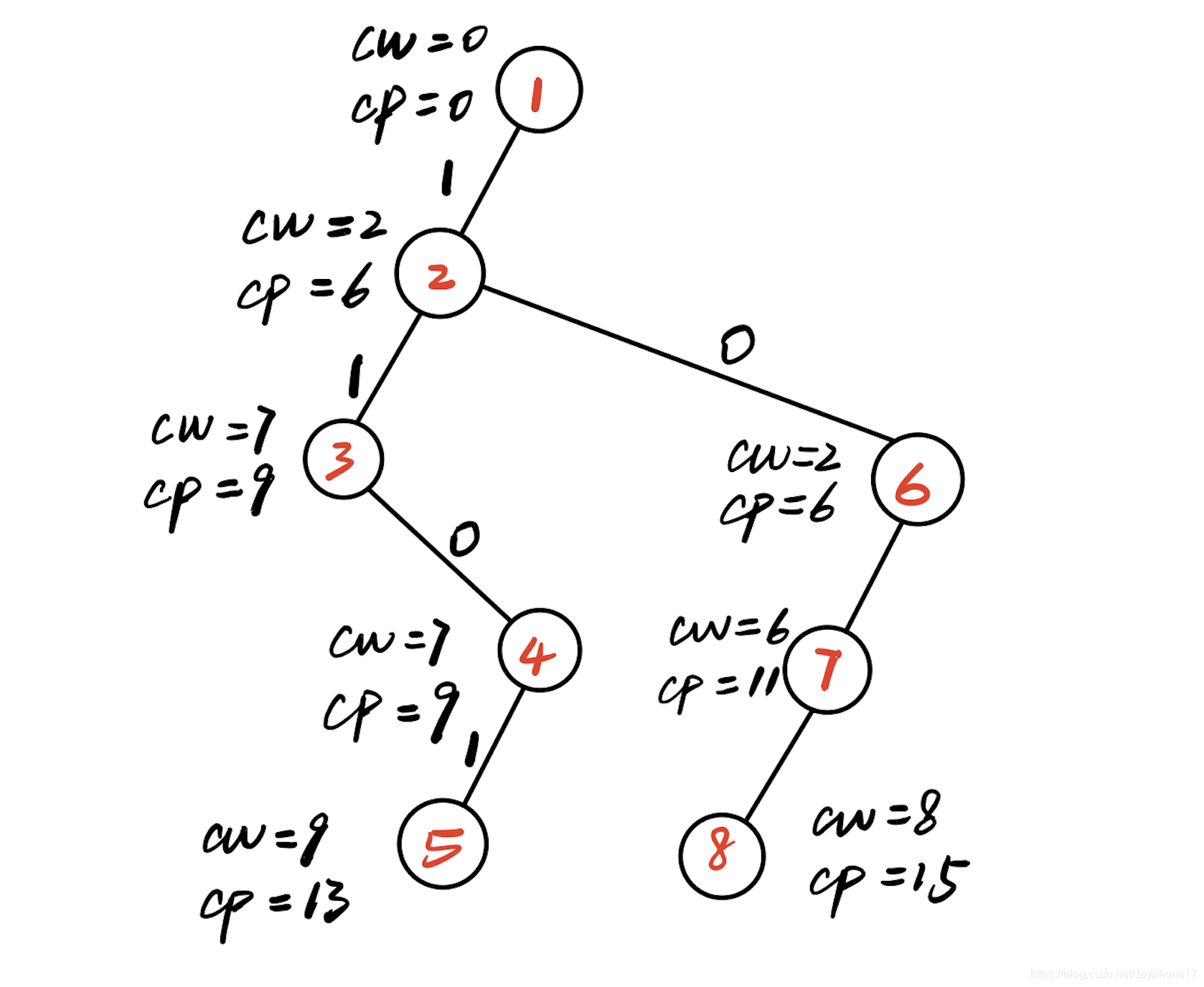
（11）判断7号结点，cw+w[4]=8<W，满足约束条件，扩展左分支，生成8号结点。

此时t=5>n，搜索结束，找到一个最优解，更新bestp=15，8号结点成为死结点，开始回溯。

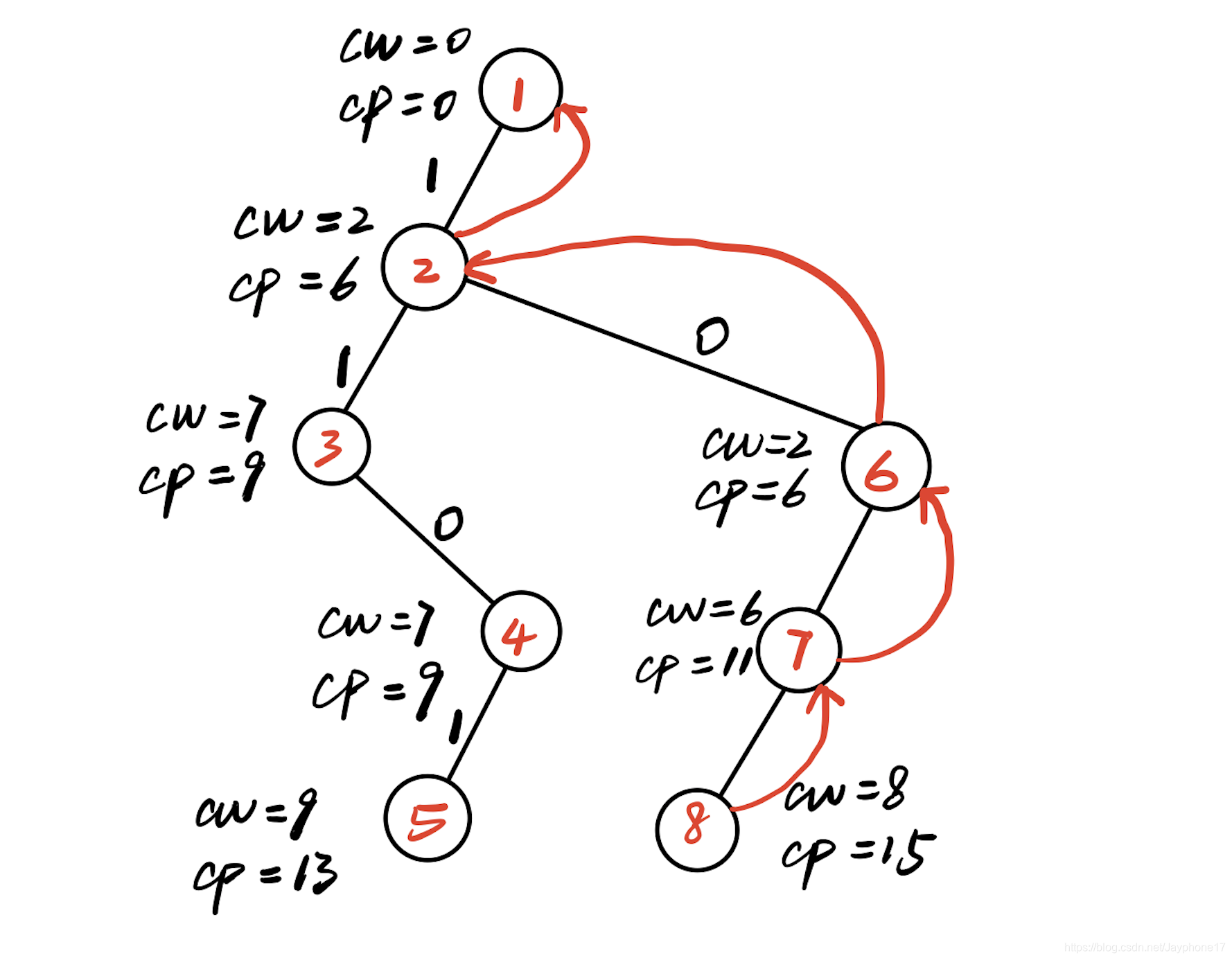
（12）回溯到7号结点，此时没有剩余物品，rp=0，cp=11，cp+rp=11<bestp=15，不满足限界条件，不扩展7号结点的右子树。7号结点成为死结点。

（13）回溯到6号结点，此时剩余一个物品，rp=4，cp=10，rp+co=14<bestp=15，不满足限界条件，不扩展6号结点的右子树。6号结点成为死结点。

（14）回溯到2号结点，此时左右孩子都已经考察过，所以成为死结点。

（15）回溯到1号结点，此时剩余3个物品，rp=12，cp=0，rp+cp=12<bestp=15，不满足限界条件，所以不扩展1号结点的右子树，1号结点成为死结点。此时搜索结束。

四、伪代码

（1）计算上界

上界是指计算已经装入物品的价值cp与剩余物品的总价值rp之和。

double Bound(int i) //计算上界
{
    int rp=0;
    while(i<=n) //计算剩余物品重量和
    {
        rp+=v[i];
        i++;
    }
    return cp+rp;
}

（2）按照约束条件和限界条件进行搜索

t表示当前扩展结点在t层，cw表示当前已经放进购物车的重量和，cp表示已经放进购物车的价值和。

如果t>n，表示已经到达叶子结点，记录最优值，返回结果。

否则，判断是否满足约束条件，满足搜索左子树。

判断是否满足限界条件，满足搜索右子树。

void Backtrack(int t) //回溯函数
{
    if(t>n)//已经到达了叶子结点
    {
        for (int j=1;j<=n;j++)
        {
            bestx[j]=x[j]; //记录编号
        }
        bestp=cp;//保留当前最优值
        return;
    }
 
    if(cw+w[t]<=W)//如果满足条件，扩展并且搜索左子树
    {
      x[t]=1;
      cw+=w[t];
      cp+=v[t];
      Backtrack(t+1);//回溯
      cw-=w[t];
      cp-=v[t];
    }
 
    if(Bound(t+1)>bestp)//如果满足限界条件，搜索右子树
    {
      x[t]=0;
      Backtrack(t+1);//回溯
    }
}

 

五、源代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define M 105
 
int n;//表示物品个数
int W;//表示购物车总载重量
double w[M];//表示对应物品重量
double v[M];//表示对应物品价值
bool x[M];//用来判断是否是否放入购物车
double cw;//当前放进购物车总重量
double cp;//当前放进购物车总价值
double bestp; //当前最优值
bool bestx[M]; //当前最优解
 
double Bound(int i) //计算上界
{
    int rp=0;
    while(i<=n) //计算剩余物品重量和
    {
        rp+=v[i];
        i++;
    }
    return cp+rp;
}
 
void Backtrack(int t) //回溯函数
{
    if(t>n)//已经到达了叶子结点
    {
        for (int j=1;j<=n;j++)
        {
            bestx[j]=x[j]; //记录编号
        }
        bestp=cp;//保留当前最优值
        return;
    }
 
    if(cw+w[t]<=W)//如果满足条件，扩展并且搜索左子树
    {
      x[t]=1;
      cw+=w[t];
      cp+=v[t];
      Backtrack(t+1);//回溯
      cw-=w[t];
      cp-=v[t];
    }
 
    if(Bound(t+1)>bestp)//如果满足限界条件，搜索右子树
    {
      x[t]=0;
      Backtrack(t+1);//回溯
    }
}
 
void Knapsack(double W,int n)
{
    //初始化
    cw=0;
    cp=0;
    bestp=0;
    double sumw=0;
    double sumv=0;
    for (int i=1;i<=n;i++)
    {
        sumw+=w[i];
        sumv+=v[i];
    }
    if(sumw<=W)
    {
        bestp=sumv;
        cout << "放进购物车的物品最大价值是：" << bestp << endl;
        return;
    }
    Backtrack(1);//回溯
    cout << "放入购物车的物品最大价值是：" << bestp << endl;
    cout << "放进购物车的物品的序号是：";
    for (int i=1;i<=n;i++)
    {
        if(bestx[i]==1)
        {
            cout << i << " " ;
        }
    }
    cout << endl;
}
int main()
{
    cout << "请输入物品的个数："  << endl;
    cin >>n;
    cout << "请输入购物车的重量W：" << endl;
    cin>>W;
    cout << "请依次输入没个物品的重量w和价值v，用空格分开";
    for (int i=1;i<=n;i++)
    {
        cin >> w[i] >> v[i];
    }
    Knapsack(W,n);
    return 0;
}

 

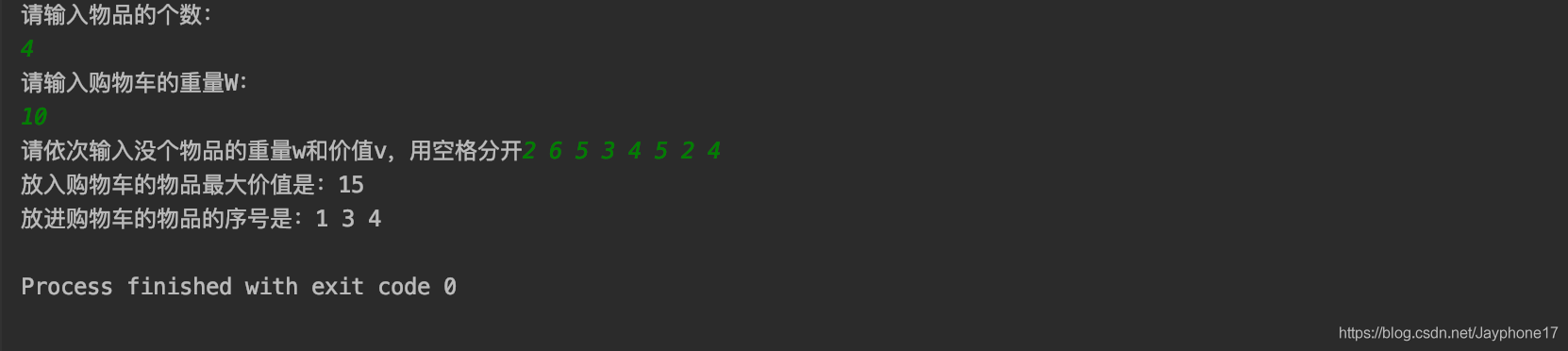
六、运行结果