短时交通速度预测SCG：A Novel STFSA-CNN-GRU Hybrid Model for Short-Term Traffic Speed Prediction_交通流 速度预测

A Novel STFSA-CNN-GRU Hybrid Model for Short-Term Traffic Speed Prediction

短时交通速度预测的STFSA-CNN-GRU混合模型

介绍

卷积神经网络门控递归单元（CNN-GRU）的混合时空特征选择算法（STFSA）

背景：私家车数量急剧增加，导致现有道路网的容量过大，从而导致交通堵塞

短时交通速度是衡量城市交通流的一个重要参数，是指根据短时的历史交通速度数据预测未来道路交通速度。

目前基于深度学习的交通速度预测方法的研究主要集中在短期相关性上，导致对时间序列周期性的学习不足，而很少考虑交通速度数据的时空相关性。此外，仅使用一个模型难以提高短期交通速度预测的准确性，即，必须将时空相关性与另一个准确模型相结合，以产生能够提高交通速度预测的混合模型。

因此，本研究的目的是将时空特征选择算法（STFSA）与卷积神经网络门控递归单元（CNN-GRU）相结合，提出一种混合交通速度预测模型（STFSA + CNN-GRU，简称SCG）。该模型克服了单一模型的局限性，充分利用了交通数据的时空特性，提供了比目前其他模型更准确的交通速度预测。因此，本研究的主要贡献是通过结合CNN的优点（即，从卷积层和池化层提取深度特征用于模型训练），具有前向GRU和反向GRU的优点（即，捕获数据的定时和长距离依赖性）。这可以为ITS中的交通速度预测提供一种替代方案。

方法论

A.交通数据的时空相关性分析

当前车速在时间维度上一般是历史车流状态的延续，即车速的变化具有一定的周期性。

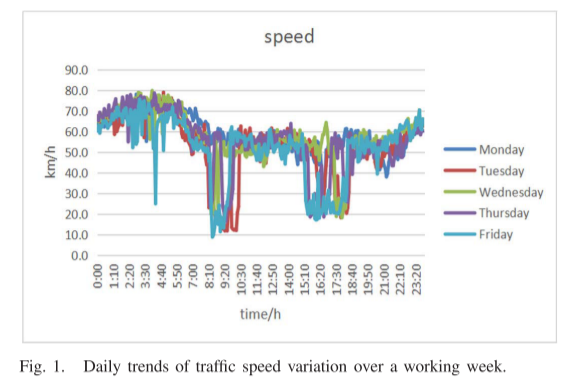
该曲线直观地反映了城市道路交通速度在时间维度上的周期性和相似性，可用于预测未来交通速度趋势。

城市道路网络也是由相互连接的道路组成的，在这样的网络上的任何地方都是空间可达的。因此，交通信息收集设备安装在中间街区和交叉口，以从不同的位置获得不同的参数。从统计学的角度来看，空间上两点之间的距离越近，相似度越高。横截面交通流之间的相关性受多种因素影响：定性分析表明，当两个横截面靠近上下游时，它们之间的相关性较强，而随着它们之间距离的增加，随着车辆进入、离开和在流内改变路线，相关性减弱

B.时空结合的候选选择算法

STFSA算法是一种时空特征选择算法，用于确定最佳的输入时间间隔和空间数据量。该算法通过相关性分析和时空特征选择算法（STFSA）确定有效的输入数据，通过 STFSA 确定佳的输入数据的时间滞后和空间路段的数量

在实际情况下，道路交通流的影响是复杂的，道路交通受多种因素的影响，既有时间相关的影响因素，也有空间相关的影响因素。可以分析交通速度数据中的空间-时间相关性，然后根据这些相关性映射到预测问题的程度进行排名。选取相关性最大、输入时滞最佳的几个监测点的数据。以这种方式，交通流的时空矩阵被重构为预测模型的输入特征。因此，在确定合理的输入数据大小之后，构建预测模型，并且对所得到的相关性数据进行排序，从而使得能够评估对验证数据的预测性能，使得可以使用STFSA算法来确定最佳输入数据大小。

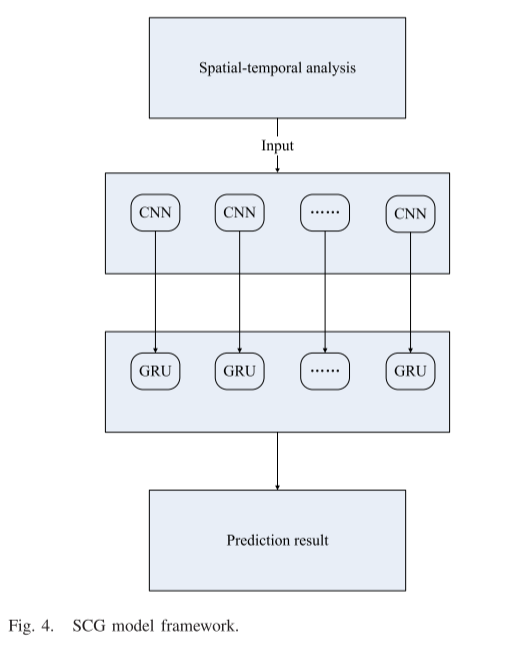
图4展示了应用时空特征选择算法的整个预测过程。时空特征选择算法使用预测算法本身作为评估特征子集的算法的一部分来搜索一个好的子集。将预测算法看作一个黑盒子。预测算法在训练数据集上运行，通常分为实际训练集和验证集，并从数据中删除不同的时间或空间特征。评价最高的特征子集被选择为运行预测算法的最终集合，并给出最终的推荐时空输入。

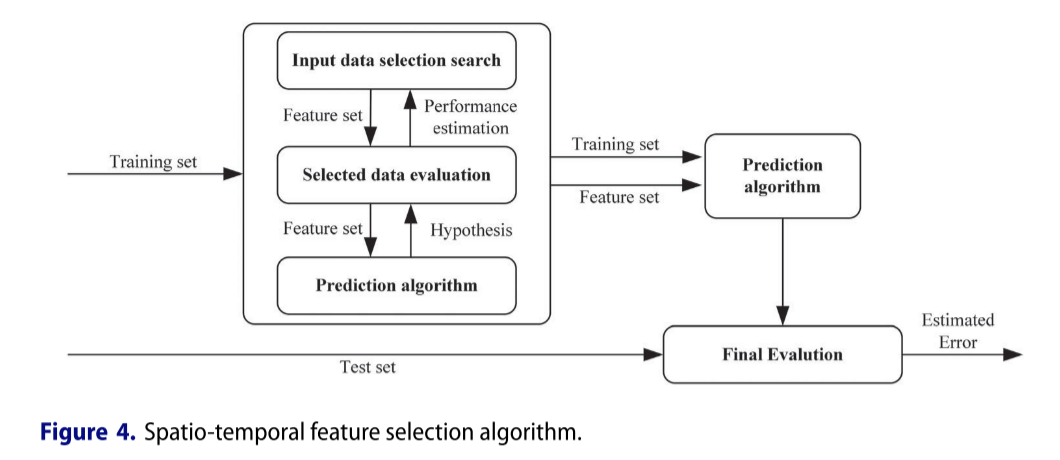
在交通速度数据分析中，预测模型充分利用选定的数据作为已知信息建立矩阵，并根据矩阵信息预测未来的交通速度。在这项研究中，皮尔逊相关系数被用作评估相关性强度的标准，相关性定义如下（等式(1))：

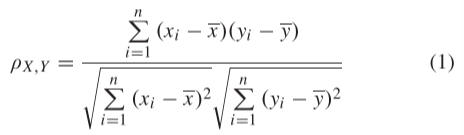
其中，x_i和y_i表示两个交通速度序列，皮尔逊相关系数的值表示两个时间序列之间的相关性。系数值越接近1，两个序列之间的相关性就越大。

STFSA是一种用于搜索网络输入的算法，该算法在验证数据集上显示出最高的预测精度，其中添加的α|d|术语是网络复杂性和预测准确性之间折衷。STFSA可以由以下公式（Eq.(2))：

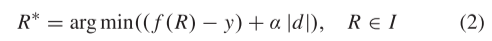
STFSA的具体计算过程如下：

步骤1：以初始化的相关时间长度和空间相关数据个数R1作为输入时空数据量d，利用MAPE对输入数据进行评估，得到验证集的预测误差E。最好的输入数据R^*是R1。

步骤2：将算法的初始参数t的值设置为0。当t小于算法停止控制的参数T时，将另一算法的初始参数s的值设置为0。当s小于S时，时滞改变，并且相关时间长度和空间相关数据的数量R1在数据集I中不重复。

步骤3：重复步骤1，将相关时间长度和空间相关数据数R ^作为新的输入时空数据量d ^，得到验证集的预测误差E ^，使用MAPE对输入数据进行评估。

步骤4：如果E + a|d‘| < E + a|d|，将s初始化为0，将E的值改变为E ^，并将d的值改变为d ^。此时，最好的输入数据R是R ^。如果E + a|d| < E + a|d|，s的值增加1，然后退出循环。

步骤5：初始化s。当s小于S时，改变添加到计算中的道路段的数量，并且不在数据集I中重复找R^。然后重复步骤3和步骤4。

步骤6：参数t的值每次增加1，直到t >= T，算法结束，得到最优输入数据R *。

在分析交通速度数据的空间和时间相关性之后，选择与预测点具有最高相关性的四个监测点。然后，所提取的交通速度数据（以时间和空间维度表示）被扩展以构建具有交通速度信息的时空相关矩阵，如下：

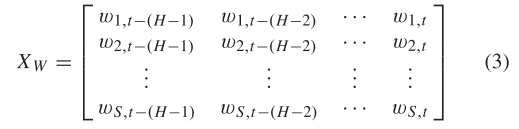
其中H表示输入数据的时滞，S表示通过空间相关分析选择的检测点的数量。

C.CNN模型介绍

通过构建在多层高级特征中表达抽象语义信息的多层网络，利用深度神经网络在多层中表示目标，从而能够生成更鲁棒的特征。CNN是一种具有卷积结构的深度神经网络，它减少了深度网络占用的内存量。CNN是一种多层监督学习神经网络，其中隐藏层中的卷积层和池采样层是特征提取功能的核心。CNN中的三个关键操作发生在输入空间的局部感受野、权重共享层和池化层，有效减少了网络参数的数量，缓解了模型过拟合的问题。

与传统技术相比，CNN具有独特的优势，如良好的容错性，并行处理能力和自学习能力。因此，它可以处理具有大的缺陷和失真的样品。CNN通过结合局部感知区域、共享权重和空间或时间上的下采样来优化网络结构，从而在很大程度上保证了位移和变形的不变性。

卷积核由具有以下公式：

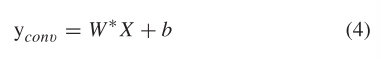
其中，k表示卷积运算，W和b分别为网络卷积层的权重和偏差。非线性映射被认为是卷积层输出处的激励层。CNN通常使用整流线性单位（ReLu）函数作为激活函数。计算方法如下：

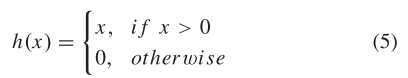
池化层对输入特征进行下采样，并使用池化函数计算网络中一个小区域的统计特征，作为位置的输出。通常有两种池化方法：平均池化和最大池化，在本研究中采用后者。假设池化窗口大小为p × q，计算方法如下：

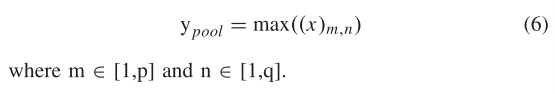
下采样和上采样

缩小图像（或称为下采样（subsampled）或降采样（downsampled））的主要目的有两个：

1、使得图像符合显示区域的大小；

2、生成对应图像的缩略图。

放大图像（或称为上采样（upsampling）或图像插值（interpolating））的主要目的是：放大原图像,从而可以显示在更高分辨率的显示设备上。

上采样和下采样都是一种抽象描述，其具体实现有很多种方式：

下采样：

1. 用stride为2的卷积层实现：卷积过程导致的图像变小是为了提取特征。下采样的过程是一个信息损失的过程，而池化层是不可学习的，用stride为2的可学习卷积层来代替pooling可以得到更好的效果，当然同时也增加了一定的计算量。
2. 用stride为2的池化层实现：池化下采样是为了降低特征的维度。如Max-pooling和Average-pooling，目前通常使用Max-pooling，因为他计算简单而且能够更好的保留纹理特征。

上采样：

1. 插值，一般使用的是双线性插值，因为效果最好，虽然计算上比其他插值方式复杂，但是相对于卷积计算可以说不值一提，其他插值方式还有最近邻插值、三线性插值等；

2. 转置卷积又或是说反卷积(Transpose Conv)，通过对输入feature map间隔填充0，再进行标准的卷积计算，可以使得输出feature map的尺寸比输入更大；相比上池化，使用反卷积进行图像的“上采样”是可以被学习的（会用到卷积操作，其参数是可学习的）。

   

D.GRU简介

GRU是递归神经网络中的一种门控机制，它可以学习相对长期的依赖关系，而不会出现梯度消失和梯度爆炸的问题。

GRU和LSTM是两种类型的递归神经网络（RNN），但GRU的网络结构比LSTM的网络结构更简单，因为GRU将LSTM的输入门和遗忘门组合成一个门，称为更新门。在GRU网络中，LSTM网络中没有内部状态和外部状态的划分;相反，梯度消失和梯度爆炸的问题通过直接添加当前网络状态ht和前一个状态ht-1之间的线性依赖关系来解决。因此，GRU保留了LSTM网络的功能，但其结构更简洁。本研究中使用的GRU结构如图2所示：

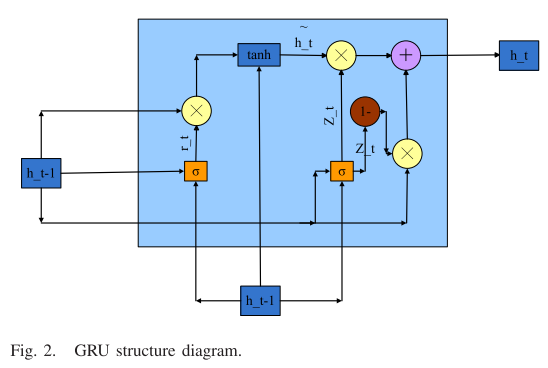
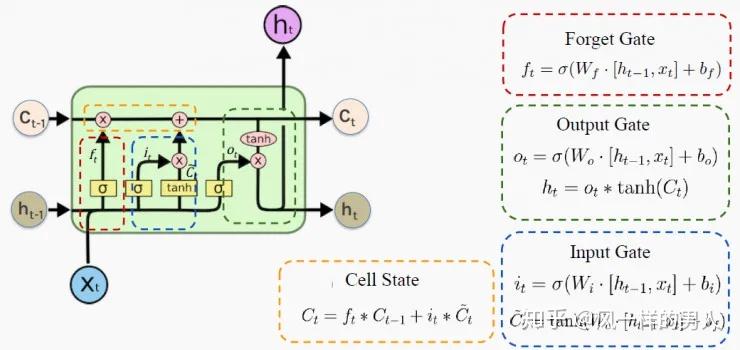
在上式中，Z_t表示更新门，r_t表示复位门。h_t '表示当前神经元中的未决输出值，σ表示sigmoid函数。W_z、W_r、W是每个门的权重。

E.STFSA-CNN-GRU混合模型简介

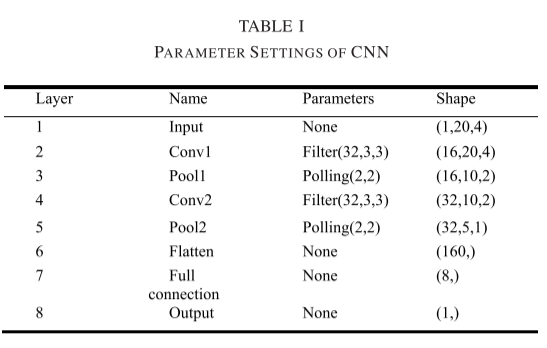
在这里，提出了一种结合CNN和阈值控制回路单元的短期交通速度预测模型。参考是最早商业化的CNN结构LeNet-5，所有卷积核的大小设置为3 × 3，池化窗口大小设置为2 × 2。基于Zhang等人的实验工作。[10]关于所需的网络深度，选择卷积层和池化层两层作为特征提取的网络结构。CNN的参数设置如表I所示。

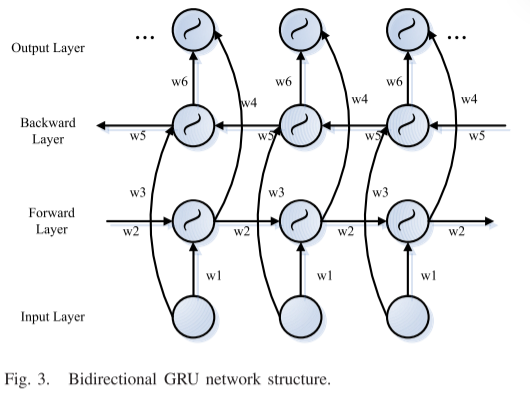
为了在GRU部分中提供更高的准确性，预测有时可能需要由先前的输入和稍后的输入联合确定。因此，构建了双向GRU网络；网络结构如图3所示。前向层和后向层连接到输出层，输出层包含在每个时间步重复使用的六个共享权重（w1-w 6）。

首先，在Forward层中计算一次，在Backward层中向后计算一次，得到并保存隐藏层每一时刻的输出，然后将Forward层和Backward层对应时刻的结果结合起来，得到最终的输出。该混合SCG模型的框架如图4所示：

F.评价指标

选择平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）作为比较这些预测算法的精度评价指标（Gu et al.，2019年）。

MAPE是相对百分比误差绝对值的平均值。

MAPE计算如下：

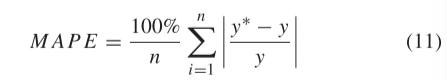
MAE是平均绝对误差，计算公式如下：

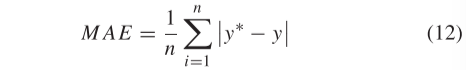
RMSE是均方根误差，并且可以如下计算：

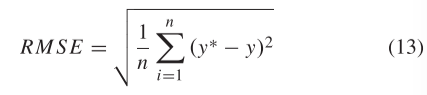
在上面的三个等式中，n是样本大小，y是预测值，y是实际值。

G.我们提出的方法的框架

本节综合了上述方法的框架，以揭示研究逻辑。如图5所示，将展示本文中提出的短期交通速度预测框架的流程图。

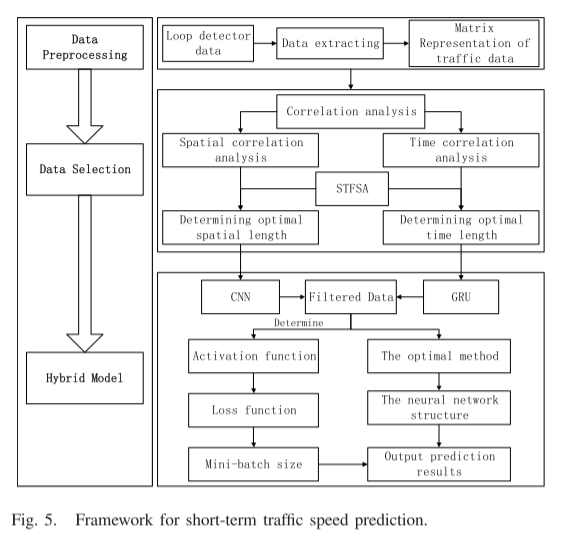
如第四节所述，对道路交通数据进行预处理，并根据其时间和空间维度将其放入矩阵。输出是模型在测试数据集上的预测输出，如第V节所述。

数据描述

这些数据是在杭州上塘至中和高架路段使用7个远程微波探测器收集的，时间为7个月(2015年6月11日至2015年11月11日)。包括三个变量：流量、密度和车道占有率。

在图6中，微波探测器的位置用红点标记。微波号码从北到南依次为：164、148、163、144、162、161。

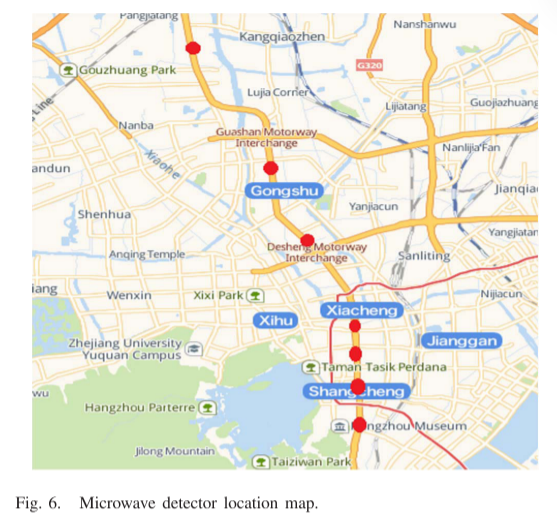
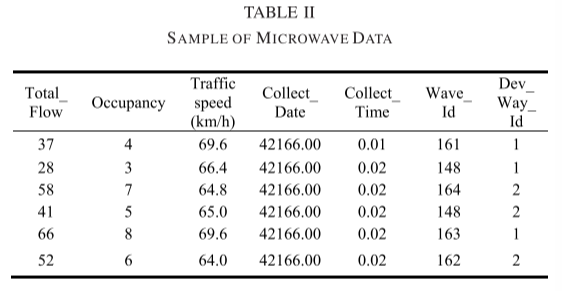
表II给出了收集的原始数据的样本，其中 “Total_Flow” 是五分钟流量，占用率是车道占用，“Collect_Date”是采集日期，“Collect_Time”是采集时间，“Wave_ID”是微波编号，“Dev_Wav_ID”是车道编号。

个案研究

A.实验环境和实验步骤

本实验使用频率为2.10 GHz的PC，CPU为A8- 5550 M，内存为4G。Python 3.6和Keras 2.1.3用于实现该模型。本实验的具体实施过程如下：

步骤1.对微波数据进行过滤，去除重复数据和差异较大的数据。选择要预测的车道的交通速度数据。

步骤2.引入STFSA分析数据的时空特性，利用与预测点相关性最高的4个监测点的数据，构建包含交通流信息的时空相关矩阵。

步骤3.将时空分析后的数据输入SCG混合模型进行分析预测。

步骤4.将预测时刻的预测交通流量作为SCG混合预测模型的输出。

步骤5.重复步骤1-4，使用来自道路的另外两个车道上的检测器的数据，以证明所开发的方法的有效性。

B.不同车道的预测结果及分析

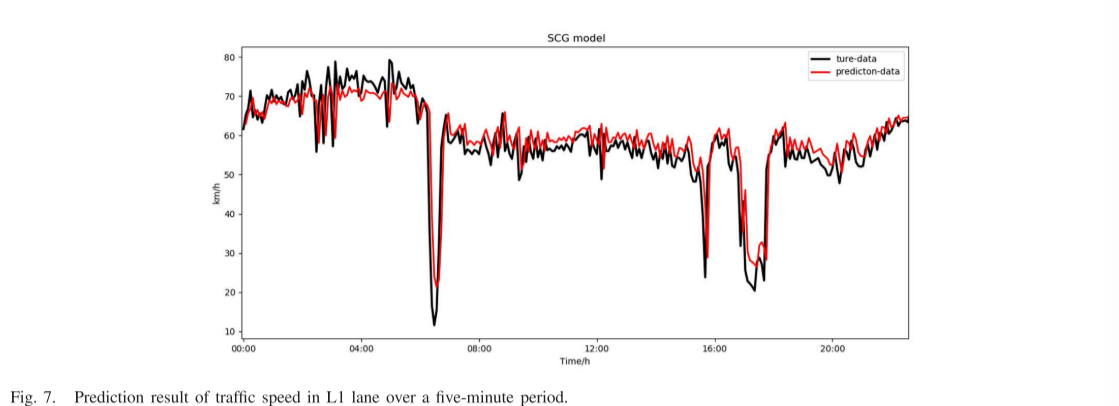
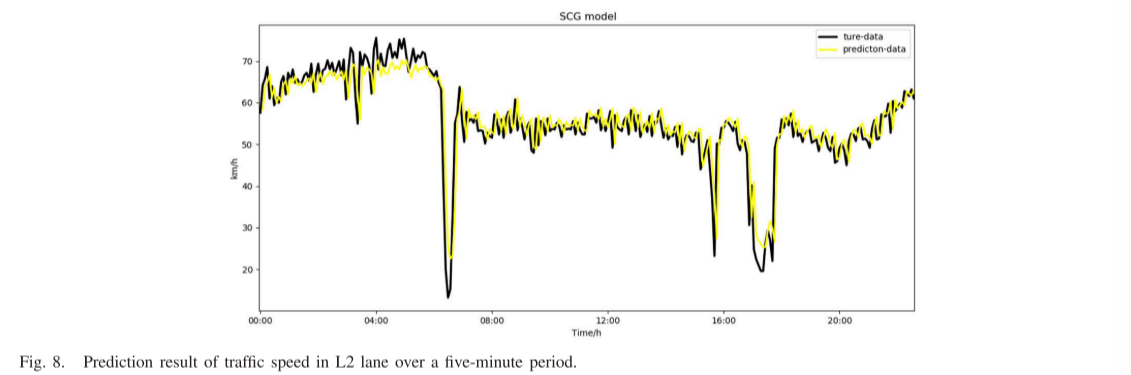
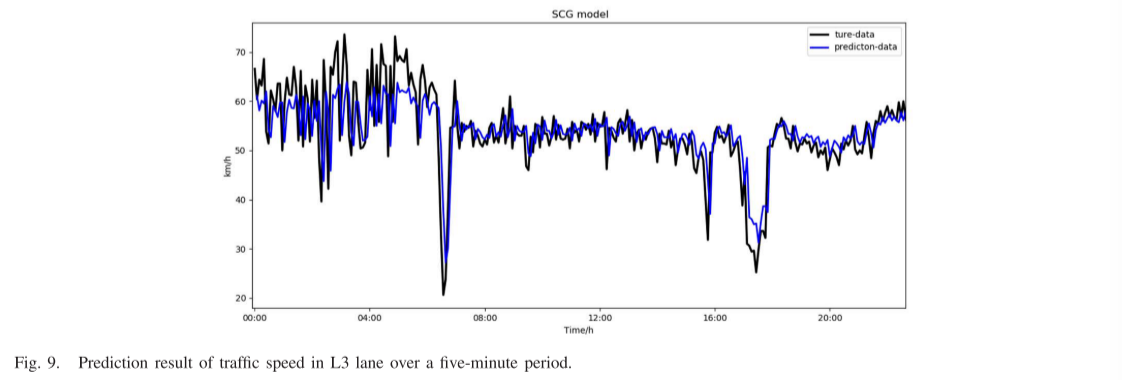
本实验建立了混合SCG预测模型，对同一路段内三车道的交通速度进行预测。图7-9分别是车道ID为1、2和3的三个车道的五分钟交通流速度预测结果。

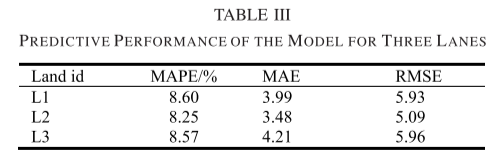
从三幅图中可以看出，预测的交通速度曲线与实际的交通速度变化基本一致：有明显的早晚高峰时段，在这段时间内，交通速度缓慢或拥堵，而在夜间其余时间，则恢复了平稳、高速的状态。三条车道的车速随着时间的推移是等量递增和递减的，早高峰、晚高峰、非高峰曲线的形状相似。三个车道的模型预测性能如表III所示。

从表III中可以看出，MAPE、MAE和RMSE的误差都处于较低水平。因此，SCG混合预测模型对不同车道上的车速都取得了较好的预测效果。

C.不同预测模型的单步和多步预测结果比较

为了验证SCG混合预测模型的适用性，将其与其他CNN、RNN、LSTM和GRU模型的性能进行了比较。因此，表四比较了SCG预测模型与其他模型的单步预测性能。

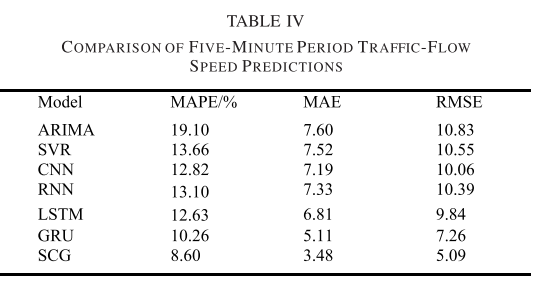
从表IV可以看出，ARIMA模型和SVR模型表现最差。CNN模型的MAE值为7.19，低于RNN的7.33，其RMSE值为10.06，也低于RNN的10.39; CNN在MAPE方面也高于RNN。因此，CNN模型在短期交通速度预测中的表现优于RNN。此外，可以看出GRU模型的预测和稳定性明显优于CNN和LSTM：GRU模型的MAE值为5.11，大幅低于CNN（7.19）和LSTM（6.81），GRU的RMSE仅为7.62，低于CNN和LSTM的RMSE。而SCG预测模型的误差最小，稳定性较好，MAE和RMSE分别为3.48和5.09，MAPE为8.60，表明该模型具有最好的稳定性和可靠性。验证了本文提出的模型的有效性和可行性。

为了进一步测试混合SCG预测模型的适用性，进行了多步预测实验，以预测随后5分钟、10分钟、15分钟和20分钟的车道区段的平均速度。如图10和11所示。

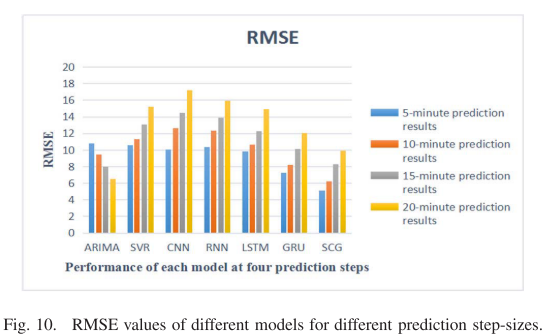
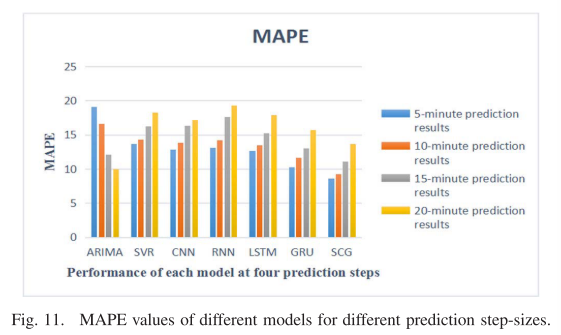
从图10和图11可以看出，随着预测步长的增加，每个模型（ARIMA模型除外）的预测精度都有所下降。而当步长为5 min和10 min时，SCG模型的预测误差最小，随着预测步长的增大，SCG模型的稳定性也最好。综上所述，SCG混合预测模型在多步预测中具有良好的适用性、准确性和稳定性。

讨论

本研究的主要成果如下：

（1）利用STFSA分析交通数据的时空特征，重构交通速度的时空矩阵作为预测模型的特征输入。

（2）结合CNN和GRU开发了交通速度预测模型（SCG），充分利用了两种深度学习模型在处理空间和时间序列数据方面的优势，取得了良好的预测效果。

（3）SCG模型与其他几种广泛使用的预测方法进行了比较，以证明其上级的适用性，准确性和稳定性。CNN和传统神经网络之间最大的区别是CNN使用卷积层和池化层。卷积层采用一个卷积核，实现同层参数的局部共享，大大减少了模型参数的数量。每个卷积核实现模型输入的特征提取，并且可以通过使用多个卷积核来提取多个特征。此外，CNN擅长提取交通数据的空间特征，尽管它们在提取交通数据的时间特征方面相对较弱。

道路交通速度性能的波动性、非线性和时空演化的特点使得预测研究工作更加复杂。基于交通流的时空分析和组合深度学习模型（SCG）将CNN与GRU相结合。GRU是LSTM NN的一种变体，已被证明可以有效地处理时间序列数据。GRU同样有效，但更简洁，因此GRU可以轻松处理交通数据中的时间特性。混合交通速度预测模型结合了神经网络和GRU的优点，充分利用了交通数据的时空特性，进一步提高了交通速度预测的准确性。

结论

本研究基于时空分析，融合CNN和GRU建立了一种用于短期交通速度预测的混合模型。

本研究的主要发现是，提出的STFSA-CNN-GRU混合模型为短期交通速度预测提供了另一种选择。这克服了单一模型的局限性，充分利用了交通数据的时空特性，实现了交通速度预测。

本研究存在以下不足：

（1）SCG模型没有考虑道路占用率、交通密度、特殊日期、突发事件等因素。因此，如果可以从不同地点收集更多的数据，SCG模型的可移植性将需要在未来的工作中进行测试和验证。

（2）该混合模型虽然实现了短时交通速度预测，但具有较好的精度，可为城市道路交通分流、诱导、管理和控制提供潜在的启示，具有一定的实用性。但在城市道路网规划、道路设施建设、交通控制系统开发等方面的适用性还有待提高，这将是我们未来面临的挑战。

参考文献：
Short-term traffic flow prediction based on spatiotemporal analysis and CNN deep learning