devbox
凡人多烦事01
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

学习自旋电子学的笔记04：模拟自旋波在弯曲磁畴壁中传播

作者：凡人多烦事01 | 2024-04-04 14:37:00

赞

踩

学习自旋电子学的笔记

文章目录



苔花如米小，也学牡丹开。----袁枚《苔》

前言

五月过去了，看到应届的学生们毕业，让我也不禁想到自己去年五月初毕业的时候，总想写点感慨啥的，但奈何自己肚里没墨水，又不善言辞，所以就以“。。。”来表达此刻的心之所思吧！本来打算在五月看一些自旋波理论相关的文章的，结果还是与看天书无二，总是不会推导文中的公式。所以还是认真的看了两篇有关自旋波模拟的文章，然后自己也尝试着复现其中一篇文章（DOI: 10.1103/PhysRevApplied.7.054016）的部分简单的微磁模拟。在此之前，还有对笔记03中的错误的补充说明。由于这是一个学习的笔记系列Blog，看过前文的读者都知道，我自己也对很多微磁模拟结果很疑惑，那么我对前面的笔记中出现的错误是这样处理的：若是错别字，标点符号之类的错误，会在原文中进行修改，若是模拟方法和代码之类的错误，就不会在原文中修改了，而是在下一个Blog中进行单独补充改正，如此做法就当做是记录自己认知的一个过程吧。

零、笔记03中错误的补充改正

1.保持电子的极化方向不变的原因

正如在上个Blog评论区中所说的部分错误描述：二、2.图4-2和三、4.FIG2（a）(b)和三、6.FIG5，其中关于电流密度为负时，SOT的参数mpy的设置都是错的。说到底，还是对于Oxs_SpinXferEvolve类的理解，以及SOT的作用效果的认识出错了。
众所周知，在HM/FM双层结构中，当流过HM层的电流反向时，由自旋霍尔效应产生的极化电子的极化方向也会跟着反向，因此极化电子对局域磁矩产生的转矩也跟着反向。 随着对微磁模拟以及Oxs_SpinXferEvolve类的认识不断深入，实际上，当改变了电流的方向（即Oxs_SpinXferEvolve的参数J的正负）后，无需再画蛇添足的去改变电子的极化方向（即Oxs_SpinXferEvolve的参数mp），只需检查修改后的转矩项是否符合预期。对应到笔记03中，即当把电流密度J设置为正数时，mpy确实和文中一样设置为-1，但当把电流密度J设置为负数时，mpy不能修改为1，否则SOT的作用效果就和J>0，mpy=-1是相同的，而不是相反的。
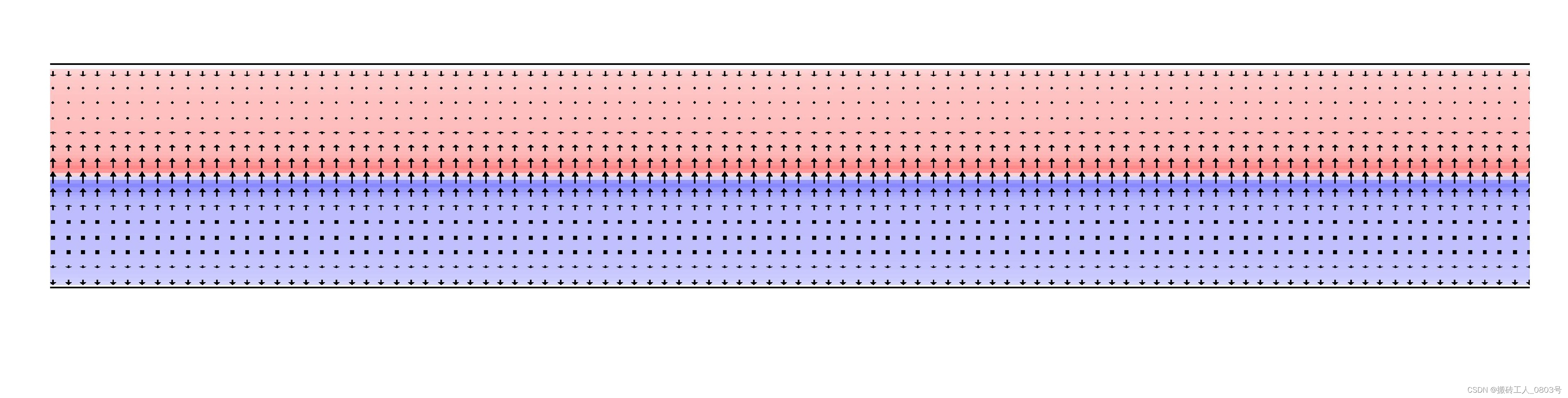
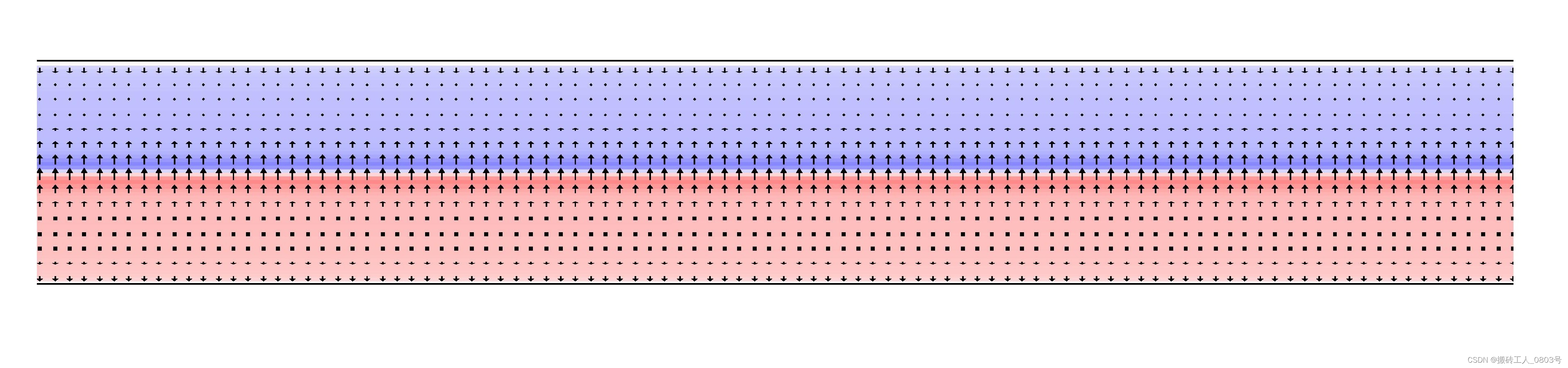
那么这个错误最直观的体现是参考原文FIG.4.（c）J>0和(f) J<0，J>0时，mx的分布为上面>0,下面<0，J<0时，mx的分布为上面<0,下面>0。经过修改后，就能对应上原文了：
当J=10e10A/m2，对应原文FIG.4.（c），不包含两端高阻尼区域的磁化状态如图：
在这里插入图片描述
当J=-10e10A/m2，对应原文FIG.4.（f），不包含两端高阻尼区域的磁化状态如图：
在这里插入图片描述

2.Oxs_SpinXferEvolve类的额外补充说明

关于Oxs_SpinXferEvolve类，这里补充一下oommf作者对它的一些额外的，官方手册中没有的补充说明，以下是来自十多年前的一封古老邮件原文：

Dear ***

Sorry for not replying sooner. I’ve been on travel the last week.

Recently, I’m using the Oxs_SpinXferEvolve specify block to carry out some
calculations. In reading the usage instruction of this block, two questions
araise in my brain:

First, in the definition of beta, it is said that “t is the free layer
thickness in meters”. Here, I’d like to know whether the free layer
thickness–t is the “spacer layer” in a spin valve, or in other words, can
the Oxs_SpinXferEvolve specify block be used to a single–layer element, for
example a cicular disk with a diameter R=500 nm and thickness d=30 nm?

Oxs_SpinXferEvolve is intended for modeling a single layer in a
multi-layer device. “t” is the thickness of the magnetically active
free-layer. In your example, t would be 30e-9 m provided the current
impinging on the layer is pre-polarized (by, presumably, the non-modeled
fixed layer), and the magnetization through the thickness of the disk is
relatively homogeneous (i.e., m(x,y,z) = m(x,y), approximately). If you
are counting on the magnetization in the disk itself to polarize the
electron flow, then you need to use a code like Antoine Vanhaverbeke’s
anv_spintevolve.

(In truth, the situation is a little more complicated, because the same
model works if the current flows first through the free layer and then
impinges on the fixed layer. See note below about position of the fixed
layer relative to the free layer and current flow direction.)

Second, inside the specify block of Oxs_SpinXferEvolve, one can adjust the
current density–J and the spin polarization direction–mp, as a function of
position. But, it seems that one can not set the current flow direction
independent of the spin polarization direction-mp, namely, the current flow
can only be along(or opposite to)the mp direction. However, to our
knowledge, for the same mp direction, different J flow directions will exert
different influence on spin evolution of the whole system. Is it the case?

In Oxs_SpinXferEvolve (at least the versions I have “released” to date)
the current flows parallel to the z-axis, which is assumed to be
coincident with the film normal. The “J” option allows you to change
the magnitude of the current, but not the flow direction. OTOH, mp is
independent of this and can be set in any direction you wish. (Recall,
however, that mp is assumed fixed with respect to time.) As stated in
the OOMMF User’s guide, “positive J produces torque that tends to align
m towards mp.” This implicitly defines the position of the fixed (i.e.,
polarizing) layer with respect to the free layer and the current flow direction.
HTH,
Mike
Michael J. Donahue
National Institute of Standards and Technology
Mathematical & Computational Sciences Division
100 Bureau Dr Stop 8910
Gaithersburg, MD 20899-8910
email: michael.donahue@nist.gov
voice: (301) 975-5424
fax: (301) 975-3553
web: http://math.nist.gov/~MDonahue/

3.时间演化器的时间步长相关补充说明

由此再延伸补充一些关于设置时间演化器的时间步长的问题：在oommf的安装目录oommf\app\oxs\local\thetaevolve下，“readme.txt”文件中Caveats部分有这样一段话：

Concerning the chosen timestep, which is not variable but fixed in this
evolverclass, numerical stability has to be considered. That is, if the timestep
is set too big, the whole system will become unstable and start to oscillate,
or at even bigger timesteps end up in deterministic chaos. To prevent this, it
is advised to start a simulation with temperature set to zero (thetaevolve
will use variable timesteps then) and check for the lower boundary of the
timesteps in this run. Choosing a timestep well below this value should be
safe.

正如笔记03的最后部分的模拟结果所述，对于时间演化器使用自由时间步长和适当的固定时间步长，所得到的模拟结果是类似的。若用户执意使用固定的时间步长，那么如何对固定时间步长取值也是一个问题。 其实正如上面的补充说明那般，当演化器采用自由的时间步长来求解LLG方程时，随着时间的演化，自由可变的时间步长会逐渐趋向于一个固定的值，这个值就是用户需要设置的固定的时间步长的上限值。用户可以通过时间驱动器的输出Last time step选项来查看时间演化器每一次迭代所选取的时间步长，当该值稳定时即是上限值。 若用户设置的固定的时间步长大于这个上限值，则会使模拟结果出错；若小于这个上限值，则不仅不会使模拟结果更加准确，反而让求解的时间大大增加，得不偿失。
所以，设置固定的时间步长要比自由时间步长多一个步骤，为了方便起见，我自己暂且都设置的自由时间步长（即时间演化器的默认情况）。

一、文章概述和要复现的微磁模拟

1.文章概述

原文DOI: 10.1103/PhysRevApplied.7.054016，即利用自旋轨道矩（SOT）在弯曲的磁体系中铺设自旋波传输通道，它和笔记03所介绍的文章有许多相似之处，不过本文的侧重点不同：有80%左右（1-6,9-16页）是介绍如何利用SOT在弯曲的磁体系中驱动磁畴壁移动，并生成一个弯曲的条形畴壁（SDW）。有20%左右（6-9页）是介绍自旋波在这个生成的弯曲的SDW中的传播。建议在阅读本笔记之前，先看两遍原文以熟悉整个微磁模拟流程。正如文章第3页中所说的，本模拟的关键在于正确设置电子的极化方向，特别是要仔细设置在纳米线的弯曲部分的电子极化方向，如此极化电子对局域磁矩产生的转矩才能使SDW的头部移动的同时，并保持SDW的脊部不移动。

2.要复现的微磁模拟

原文采用的微磁模拟软件是LLG micromagnetic simulator，不过我并没有用过这个软件。原文在建立模型时创建的是HM/FM双层结构，而我这里为了方便起见，就采用等效的方法，只考虑FM单层结构，将其他结构层的影响等效在FM层的磁性参数中。原文还考虑了通过HM层的电流产生的奥斯特场，而我暂时不晓得如何设置，因此就没有考虑这个奥斯特场，所以得到的模拟结果和原文对比起来在某些具体的数值上不一样，但是体现的物理过程是一样，所以我觉得问题不大。
要复现的模拟有原文中的FIG.1、FIG.2、FIG.3、FIG.5、FIG.6，即只复现“Y型”磁体系相关的模拟，如下图：
在这里插入图片描述

在这里插入图片描述

二、FIG.1

从FIG.1中可以得到微磁模拟所需模型的部分几何尺寸参数，结合原文的描述，”90°Y型“是由一个左边的基底，右边的两个臂，中间的两个圆环组成的。其中圆环的外半径为400nm，环宽为100nm；两个臂之间的夹角为90°，基底和两臂的宽度也为100nm，虽然它们的长度是相同的，但是数值是没有明确说明的；基底和两臂突出的上下两条导线叫做盘“Pad”，盘的长度为150nm，宽度为20nm。
我们都知道在oommf中建立的模型都需要放在一个长方体状的容器中，以此来约束所建立模型的最大几何空间，但是原文中并没有关于这个模型的基底和两臂长度的具体几何数值，不过从FIG.1中通过像素比例尺的关系，可以得到FIG.1中的基底和两臂长度为183nm。此外，也可以看出圆环的角度为45°（即完整的圆环的1/8）。对于这种复杂的几何模型，使用图像来建立模型是非常方便的，按照1nm对应1像素的关系可以画出这个原始图像如下：
在这里插入图片描述
紧接着还要在不缩放的情况下对这个原始图像进行裁剪（找到模型占用的最大几何空间）和颜色填充（方便在程序中按颜色划分区域），把处理过后的最终效果图像命名为“Y_model.png”，如下所示：
在这里插入图片描述
该图像大小为712X630像素，即是oommf中容器设置的最大尺寸为712X630nm，从这个图像中还可以知道上圆环的圆心在(333,200)像素，下圆环的圆心在(333,500)像素，整个“Y模型”按颜色被分为了五个区域：红色（#FF0000）表示基底区域，绿色（#00FF00）表示上臂区域，蓝色（#0000FF）表示下臂区域，黄色（#FFF200）表示上圆环区域，紫色（#FF00FF）表示下圆环区域，之所以要对两个圆环水平均分，是为了方便在后面的代码中正确的设置这两个弯曲区域的电子极化方向。至于白色背景就表示没有磁性的区域。
这里有必要注意一下，图像的像素坐标系与微磁模型的单元格坐标系之间的转换关系：图像的像素坐标原点在左上角，向右为+x方向，向下为+y方向；微磁模型的坐标原点在左下角，向右为+x方向，向上为+y方向。于是就有了这样的关系：X单元格=X像素，Y单元格=图像的高度-Y像素。
从FIG.1中还可以得到当开关S1和S3相连接时，电流从上臂流到基底时电流密度的分布，那么去除FIG.1中的冗余信息，在通过拼剪得到712X630像素大小的电流密度分布图像，并命名为“S1_S3_current.png”，如下所示：
在这里插入图片描述
由于没有处理得多么精细，所以乍一看有点和原文对不上，但是只要“Y_model.png”中每一个像素都能在“S1_S3_current.png”中找到对应像素的电流密度大小就可以了。原文中只有开关S1和S3相连接时的电流密度分布，而没有S1和S3相连的图像，而我又不会计算这种电流密度的分布，所以FIG.2(h)和后面的SDW在下臂的情况就不能复现了。
“S1_S3_current.png”中的电流密度整体上是按两种颜色分布的，即当像素的G=B!=R时，则认为该像素对应正J，当像素的R=G!=B时，则认为该像素对应负J，对于图像中的其他杂色（白/灰色、黑色等不在两种颜色范围内的颜色），则认为该像素对应J=0。此外颜色分量是按照线性变化的，故电流密度与颜色分量的总和也是成线性关系的，具体的换算方法见后文的代码。
在FIG.1中，电流总体是按照红色箭头指示的那样从坐标系的+x流向-x方向的，因此在颜色&电流密度比例尺中也是用负数表示这个方向的电流，但是在代码中设置电子的极化方向时，应该把电流流动的方向作为正方向，即在代码中将像素换算为电流密度数值时，需要额外乘以-1。有了在HM层中电流的流动方向，还可以得到由SHE产生的极化电子的极化方向，即按照原文中的关系式“σ = -J X Z”来逐单元格设置：在基底区域中，红色箭头向左，故电子的极化方向即mp为(0,-1,0)；在上臂区域中，电子的极化方向即mp为(cos-45°,sin-45°,0)=(0.707,-0.707,0)；在下臂区域中，电子的极化方向即mp为(cos-135°,sin-135°,0)=(-0.707,-0.707,0)；在上圆环区域中，电子的极化方向为圆心指向该区域的单元格，即mp=(X单元格-X圆心,Y单元格-Y圆心,0)；在下圆环区域中，电子的极化方向为该区域的单元格指向圆心，即mp=(X圆心-X单元格,Y圆心-Y单元格,0)。

三、 FIG.2

1. FIG.2(a-b)

“Y模型”需要在单畴的情况下，在盘A的50X20nm范围内，即盘A的1/3长度范围内施加外加磁场以用于生成种子反磁畴，该矩形区域的下顶点设为A，按照逆时针方向，其他三个顶点依次是B，C，D。从图像“Y_model.png”中可以很轻松的找到这个矩形区域的四个顶点对应的像素，换算到微磁模拟中的单元格坐标：A(618,580)nm，B(654,616)nm，C(639,630)nm，D(604,594)nm，那么这四个顶点的连线方程为：线段AD：y=-1* x+1* 618e-9+580e-9，线段BC：y=-1* x+1* 654e-9+616e-9，线段AB：y=1* x-1* 618e-9+580e-9，线段CD：y=1* x-1* 639e-9+630e-9，这四条线段围成的矩形区域就是要施加外加磁场的区域。
该外加磁场的函数形式为Hi=1.4142T * sin(2pi2.5GHz*t)，方向为与盘A的长度方向垂直，且与xy平面成45°并指向+z方向，该磁场的作用时间为200ps。该sin函数的标准形式如下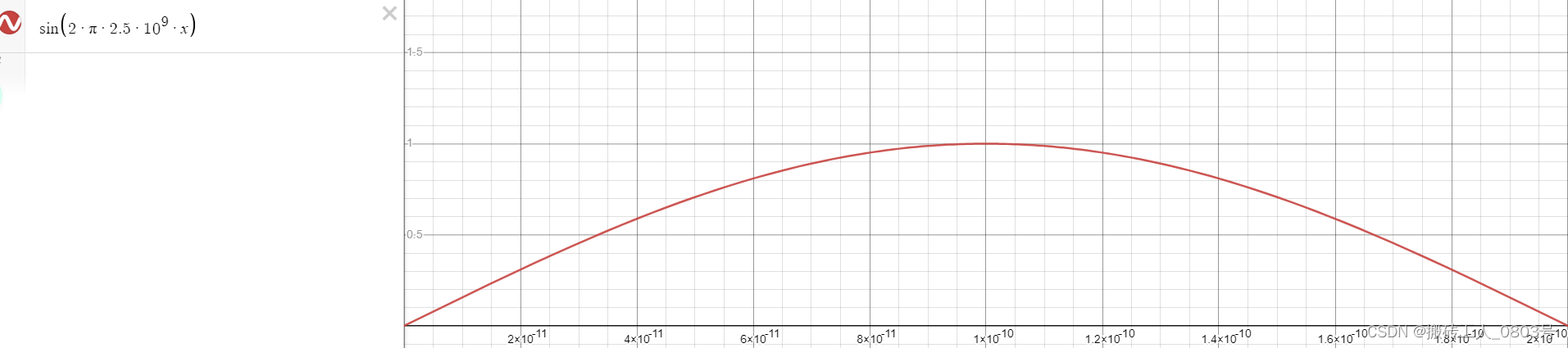：请添加图片描述
接着需要计算该外加磁场的三个分量，通过简单的几何关系可知：外加磁场的振幅|H|为1.4142T ，其z分量Hz=|H|*sin45°，在xy面的投影的模长为|Hxy|=|H|*cos45°，该投影与x轴的夹角为135°，与y轴的夹角为45°，故可得外加磁场的x分量Hx=|Hxy|cos135°，y分量Hy=|Hxy|cos45°。之后这三个分量还要设置为按sin形式随时间变化，那么只需将这个变化函数当做三个分量的系数，直接分别乘上去即可。
综上，生成种子反磁畴所使用的微磁模拟mif文件如下：

# MIF 2.2

#################
#author:YQYUN
#date:22/5/20
#desc:使用图片生成的Y型FM单层体系
#desc:在Y上臂的盘A（50*20nm）中生成种子反磁畴
#desc:无电流
#desc:指向+z方向,且与xy平面成45度的外加磁场：1.4142T *	sin(2 * pi * 2.5GHz * t)，持续200ps（四分之一个周期）
#################

set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]

#使用时间驱动器的总共运行时间为200e-12s
Parameter run_time  200e-12
#每个阶段5e-12s
Parameter stage_time  5e-12
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]

#指定输出数据的格式和精度
SetOptions {
	comment "将矢量场输出的数据格式设置为ASCII文本格式（默认为b8格式）"
	vector_field_output_format {text %#.17g}
}

#容纳Y型磁体系的容器尺寸：712*630*1nm
Parameter Y_model_x 712
Parameter Y_model_y 630
Parameter Y_model_z 1
set Y_model_x [expr {$Y_model_x*1e-9}]
set Y_model_y [expr {$Y_model_y*1e-9}]
set Y_model_z [expr {$Y_model_z*1e-9}]

#单元格尺寸：2*2*1nm（单元格尺寸小于交换长度Lex=8.4nm）
Parameter xcell 2
Parameter ycell 2
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]

#定义纳米线形状，按照DMI示例文件中的形式，需要使用Oxs_MultiAtlas类来定义容器
Specify Oxs_MultiAtlas:atlas [subst { 
	atlas { Oxs_ImageAtlas:world { 
	xrange {0 $Y_model_x}
	yrange {0 $Y_model_y}
	zrange {0 $Y_model_z}
	image Y_model.png
	viewplane "xy"
	comment "依次是：左边基础区域，上圆弧区域，下圆弧区域，右边上臂区域，右边下臂区域，无磁性的区域"
	colormap {
	#FF0000 baseRegion
	#FFF200 topArcRegion
	#FF00FF bottomArcRegion
	#00FF00 topArmRegion
	#0000FF bottomArmRegion
	default no_magneticRegion
	}
	matcherror 0.2
}}
}]

#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
	cellsize {$xcell $ycell $zcell}
	atlas :atlas
}]

#定义交换能（15pJ/m）
Specify Oxs_UniformExchange {
	A 15e-12
}

#定义单轴各向异性能（垂直方向，0.8MJ/m3）
Specify Oxs_UniaxialAnisotropy {
	K1 0.8e6
	axis {0 0 1}
}

#定义退磁能
Specify Oxs_Demag {}

#定义DMI能（文中IDMI强度为2.0mJ/m2）
set D 2.0
#根据文章中所说的畴壁中磁矩指向为正指向负，对应在此代码中则将D改变符号
set D [expr {$D * -1}]
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
	default_D $DD
	atlas :atlas
	comment "按区域分配DMI系数"
	D {
	baseRegion baseRegion $DD
	topArcRegion topArcRegion $DD
	bottomArcRegion bottomArcRegion $DD
	topArmRegion topArmRegion $DD
	bottomArmRegion bottomArmRegion $DD
	no_magneticRegion no_magneticRegion 0
	}
}]

#定义饱和磁化强度Ms（580kA/m）
set Ms 5.8e5

###########施加用于形成种子反磁畴的sin形式的外加磁场###########

#sin形式的外加磁场的振幅，这里的单位为mT
set Happ 1414.2

#sin形式的外加磁场的频率，这里的单位为GHz
set frequency 2.5

#对初始的矢量场appliedFiled进行变化，
#使其成为外加磁场（+z方向，且与xy平面成45度）：H= 1.4142T * sin(2 * pi * 2.5GHz * t)
proc transformExcitationFiled { total_time } {
	global frequency pi
	set t $total_time
	#计算w=2*pi*f，并把单位顺便转化为GHz
	set w [expr {2 * $pi * $frequency * 1e9}]
	set sinwt [expr {sin($w * $t)}]
    set coswt [expr {cos($w * $t)}]
	#计算x方向的磁场分量及其对时间的导数
	#即x方向Hx*sinwt
	set Hx $sinwt
	set dHx [expr {$w * $coswt}]
	#其余两个方向也按sin形式变化，如此保证了H的振幅按照sin形式变化
	#即|H|*sin(wt)=sqrt([Hx*sin(wt)]^2 + [Hy*sin(wt)]^2 +[Hz*sin(wt)]^2)
	set Hy $Hx
	set dHy $dHx
	set Hz $Hx
	set dHz $dHx
	#返回6个元素的列表，即变换矩阵的3个主对角元素及其3个导数
	return [list $Hx $Hy $Hz $dHx $dHy $dHz]
}

#指定施加外加磁场的区域（后面转化为磁场）：H=(Hx Hy Hz)，其他区域H=(0 0 0)
proc setAppliedFiled { x y z } {
	global Happ pi
	#把盘A的方形区域内作为外加磁场的施加范围，注意：从模型图像中找到的像素y坐标转化为单元格的y坐标需要相应变换
	#该方形区域的四个顶点分别为：下：A(618e-9,580e-9),右：B(654e-9,616e-9),上：C(639e-9,630e-9),左：D(604e-9,594e-9)
	#首先划分一个大的方形范围来包围盘A的方形区域
	if {$x >= 604e-9 && $x <= 654e-9} {
	if {$y >= 580e-9 && $y <= 630e-9} {
	#接着在这个大的区域内使用四条斜线段（斜率为±1）包围盘A的方形区域
	#线段AD：y=-1*x+1*618e-9+580e-9，线段BC：y=-1*x+1*654e-9+616e-9
	if {$y >= -1*$x+1*618e-9+580e-9 && $y <= -1*$x+1*654e-9+616e-9} {
	#线段AB：y=1*x-1*618e-9+580e-9，线段CD：y=1*x-1*639e-9+630e-9
	if {$y >= 1*$x-1*618e-9+580e-9 && $y <= 1*$x-1*639e-9+630e-9} {
	#划分结束得到的即是盘A的方形区域,需要外加磁场
	#已知外加磁场的振幅，那么外加磁场Hx、Hy、Hz三个分量的计算方法如下：
	#①由于外加磁场与xy面成45度，所以Hz=|H| * sin(45°)
	#②外加磁场在xy面的投影模长|Hxy|=|H|cos(45°)，与x轴的夹角为135度，故Hx=|Hxy| * cos(135°)
	#③外加磁场在xy面的投影模长|Hxy|=|H|cos(45°)，与y轴的夹角为45度，故Hy=|Hxy| * cos(45°)
	#由以上等式，得Hx、Hy、Hz：
	set Hz [expr {$Happ * sin($pi / 4)}]
	set Hx [expr {$Happ * cos($pi / 4) * cos($pi * 3 / 4)}]
	set Hy [expr {$Happ * cos($pi / 4) * cos($pi / 4)}]
	return [list $Hx $Hy $Hz]
	} else {
	#其他区域无外加磁场
	return [list 0 0 0]
	}
	} else {
	#其他区域无外加磁场
	return [list 0 0 0]
	}
	} else {
	#其他区域无外加磁场
	return [list 0 0 0]
	}
	} else {
	#其他区域无外加磁场
	return [list 0 0 0]
	}
}
#使用脚本指定外加磁场的区域的矢量场
Specify Oxs_ScriptVectorField:appliedFiled {
	script setAppliedFiled
	script_args rawpt
	atlas :atlas
}

#使用此类可生成任意（局域，时变）的外加磁场
Specify Oxs_TransformZeeman [subst {
    field :appliedFiled
	comment "函数返回6个元素，是3个主对角元素及其3个导数"
	type diagonal
	script transformExcitationFiled
	script_args total_time
	comment "将默认单位A/m换算为mT"
	multiplier [expr {0.001/$mu0}]
	comment "将stage_count设为0（默认值），让模拟的所有阶段都存在该塞曼能"
	stage_count 0
}]
###########施加用于形成种子反磁畴的sin形式的外加磁场###########

###########时间演化的相关参数设置###########

#定义演化器（龙格-库塔时间演化器）
Specify Oxs_RungeKuttaEvolve:evolver {
	comment "阻尼系数0.02"
	alpha 0.02
}

#定义驱动器
Specify Oxs_TimeDriver [subst {
	evolver :evolver
	mesh :mesh
	comment "设置一个阶段的停止时间"
	stopping_time $stage_time
	comment "设置模拟包含的阶段数量"
	stage_count $number_of_stages
	comment "Y型区域之外的区域的饱和磁化强度为0"
	Ms {Oxs_AtlasScalarField {
	atlas :atlas
	values {
	baseRegion $Ms
	topArcRegion $Ms
	bottomArcRegion $Ms
	topArmRegion $Ms
	bottomArmRegion $Ms
	no_magneticRegion 0
	}
	}}
	comment "将初始磁化设置为单畴态（从盘A生成的种子反磁畴）"
	m0 {0 0 -1}
	comment "将checkpoint_interval设为-1，从而禁用检查点功能"
    checkpoint_interval  -1
}]
###########时间演化的相关参数设置###########

#每个阶段固定为5ps，模拟总共运行200ps，应该生成40个磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206
  • 207
  • 208
  • 209
  • 210
  • 211
  • 212
  • 213
  • 214
  • 215
  • 216
  • 217
  • 218
  • 219
  • 220
  • 221
  • 222
  • 223
  • 224
  • 225
  • 226
  • 227
  • 228
  • 229
  • 230
  • 231
  • 232
  • 233
  • 234
  • 235
  • 236

在开始模拟前，也可以选择把外加磁场一同输出，我这里也选择让它和磁化状态相同的输出选项，即模拟总时间为200ps，每5ps输出一次。模拟结束后，得到了40个.omf和40个.ohf矢量场文件。
对.ohf的处理如下：利用oommf命令行工具avf2odt对这40个矢量场文件提取采样区域635e-9 611e-9 - 637e-9 613e-9 -内的平均H值，并在odt添加时间列，即命令如下：

tclsh oommf.tcl avf2odt 	//主命令
-average space 	//整个区域的平均值
-region 635e-9 611e-9 - 637e-9 613e-9 -		//指定区域范围，-表示文件的默认范围
-index time s "abs($i) * 5e-12" 		//在odt文件插入时间列，$i表示当前输入文件的索引
-filesort "-ascii -increasing"  	//输入文件列表按照顺序增加来输入
-defaultpos 0 	//odt文件中不生成位置坐标列
-ipat TODO_picture\矢量图处理\*.ohf 	//输入文件所在的目录
-onefile TODO_picture\矢量图处理\averageH_t.odt		//输出的odt文件名称
-headers collapse 		//多个odt文件组合的一个odt文件，也只生成一组列标题

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9

如此得到H-t的关系如下所示：

在这里插入图片描述
对.omf的处理如下：利用mmDisp生成最佳显示配置文件，再利用oommf命令行工具avf2ppm将这40个矢量场文件按最佳显示配置转化为图片，使用的命令如下：

tclsh oommf.tcl avf2ppm	//主命令
-config TODO_picture\矢量图处理\display(NoArrow).config	//配置文件	的路径
-format B24	//指定输出图片格式为BMP
-ipat TODO_picture\矢量图处理\*.omf 	//输入文件所在的目录


  • 1
  • 2
  • 3
  • 4
  • 5

再把这些图片按每张图间隔0.5s制作生成种子反磁畴的动画来观察反磁化过程如下：

在这里插入图片描述
可以看到盘A的大部分区域都被反磁化，并且生成的畴壁大致垂直于盘A的长度方向，把最后一个.omf磁化文件重命名为"SeedDomain@PadA.omf"，作为后面模拟利用SOT驱动畴壁运动的初始磁化状态。

2. FIG.2(c-f)

当HM层通入电流后，产生SOT能驱动畴壁运动，原文中关于SOT的来源有两个：自旋霍尔效应（SHE）和Rashba效应，SHE只考虑了它的类阻尼矩，即Td= -γτH(m × σ × m)；Rashba效应只考虑了它的类场矩，即Tf=−γτR(m × σ)。那么对比Oxs_SpinXferEvolve类的类阻尼矩和类场矩的系数，可知在Oxs_SpinXferEvolve类中的参数：
①Lambda应设为1，以用于消除(m·mp)项。
②P应该等于自旋霍尔角0.13。
③Tf/Td=eps_prime/(0.13/2)，因此当Tf与Td的比值分别为0,0.1,0.2,0.3,0.4,0.5时，eps_prime分别设置为0,0.0065,0.013,0.0195,0.026,0.0325。
那么结合以上内容，在此处使用的代码如下：

# MIF 2.2

#################
#author:YQYUN
#date:22/5/20
#desc:Y型FM（下层）/HM（上层）双层磁体系
#desc:通过SHE的类阻尼项，Rashba效应的类场项，推动SDW的头部，在路径上生成SDW
#################

set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]

#使用时间驱动器的总共运行时间为6e-9s
Parameter run_time  6e-9
#每个阶段10e-12s
Parameter stage_time  10e-12
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]

#指定输出数据的格式和精度
SetOptions {
	comment "将矢量场输出的数据格式设置为ASCII文本格式（默认为b8格式）"
	vector_field_output_format {text %#.17g}
}

#容纳Y型磁体系的容器尺寸：712*630*1nm
Parameter Y_model_x 712
Parameter Y_model_y 630
Parameter Y_model_z 1
set Y_model_x [expr {$Y_model_x*1e-9}]
set Y_model_y [expr {$Y_model_y*1e-9}]
set Y_model_z [expr {$Y_model_z*1e-9}]

#单元格尺寸：2*2*1nm（单元格尺寸小于交换长度Lex=8.4nm）
Parameter xcell 2 
Parameter ycell 2
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]

#定义纳米线形状，按照DMI示例文件中的形式，需要使用Oxs_MultiAtlas类来定义容器
Specify Oxs_MultiAtlas:atlas [subst {
	atlas { Oxs_ImageAtlas:world {
	xrange {0 $Y_model_x}
	yrange {0 $Y_model_y}
	zrange {0 $Y_model_z}
	image Y_model.png
	viewplane "xy"
	comment "依次是：左边基础区域，上圆弧区域，下圆弧区域，右边上臂区域，右边下臂区域，无磁性的区域"
	colormap {
	#FF0000 baseRegion
	#FFF200 topArcRegion
	#FF00FF bottomArcRegion
	#00FF00 topArmRegion
	#0000FF bottomArmRegion
	default no_magneticRegion
	}
	matcherror 0.2
}}
}]

#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
	cellsize {$xcell $ycell $zcell}
	atlas :atlas
}]

#定义交换能（15pJ/m）
Specify Oxs_UniformExchange {
	A 15e-12
}

#定义单轴各向异性能（垂直方向，0.8MJ/m3）
Specify Oxs_UniaxialAnisotropy {
	K1 0.8e6
	axis {0 0 1}
}

#定义退磁能
Specify Oxs_Demag {}

#定义DMI能（文中IDMI强度为2.0mJ/m2）
set D 2.0
#根据文章中所说的畴壁中磁矩指向为正指向负，对应在此代码中则将D改变符号
set D [expr {$D * -1}]
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
	default_D $DD
	atlas :atlas
	comment "按区域分配DMI系数"
	D {
	baseRegion baseRegion $DD
	topArcRegion topArcRegion $DD
	bottomArcRegion bottomArcRegion $DD
	topArmRegion topArmRegion $DD
	bottomArmRegion bottomArmRegion $DD
	no_magneticRegion no_magneticRegion 0
	}
}]

#定义饱和磁化强度Ms（580kA/m）
set Ms 5.8e5

###########时间演化的相关参数设置###########

###########不均匀分布的电流密度设置###########

#更改图片的颜色代表的电流密度的正负和大小：1表示和颜色表示的电流密度大小和正负和图中描述相同，-1表示相反
#此处考虑到电子极化方向是根据电流方向（图中红色箭头方向为正，与颜色表示的相反）设置的，故此值应设为-1
set Jx_COLOR_OPERATOR_VALUE -1

Specify Oxs_ScriptScalarField:currentDensity {
	comment "自定义函数计算每个单元格的电流密度大小"
	script setCurrentDensity
	script_args relpt
	atlas :atlas
}

#读取图像文件，并转化为包含每一个像素信息的列表
set imagePixelList [ReadFile S1_S3_current.png floatimage]

#列表的第一个值表示图像的宽度
set imageWidth [lindex $imagePixelList 0]

#列表的第二个值表示图像的高度
set imageHeight [lindex $imagePixelList 1]

#列表的第三个值表示图像像素的最大值（已经归一化为 1）
set pixelMaxValue [lindex $imagePixelList 2]
if {$pixelMaxValue != 1} {
	Report "颜色分量最大值归一化后不是1，读取图片出错了！"
}

proc setCurrentDensity { rel_x rel_y rel_z } {
	global Jx_COLOR_OPERATOR_VALUE
	global imagePixelList imageWidth imageHeight
	
	#当前单元格对应的图片中像素的x坐标
	set i [expr {int(floor(double($rel_x)*$imageWidth))}]

	if {$i>=$imageWidth} {set i [expr {$imageWidth-1}]}
	
	#列表包含的RGB三元组按照从图片的左到右，上到下的顺序表示像素
	#而oommf的模型的单元格取值顺序是从左到右，从下到上，故需要处理y坐标
	set j [expr {int(floor(double(1-$rel_y)*$imageHeight))}]
	
	if {$j>=$imageHeight} {set j [expr {$imageHeight-1}]}
	
	#此处+3来跳过列表的前三个元素
	set index [expr {3*($j*$imageWidth+$i)+3}]
	
#图片中像素的RGB的值(归一化值)对应的电流密度大小如下：
#	Jx		R				G				B		
#	3e12	255(1)			133(0.52)		133(0.52)
#	2e12	255(1)			170(0.66)		170(0.66)
#	1e12	255(1)			208(0.81)		208(0.81)
#	0		255(1)			255(1)			255(1)
#	-1e12	208(0.81)		208(0.81)		255(1)
#	-2e12	170(0.66)		170(0.66)		255(1)
#	-3e12	133(0.52)		133(0.52)		255(1)
#	-3.5e12	112(0.43)		112(0.43)		255(1)
	
	#分别获取当前单元格对应图片中像素点的归一化的R,G,B的值
	#Red
	set normalizedRedValue [lindex $imagePixelList $index]
	incr index
	#Green
	set normalizedGreenValue [lindex $imagePixelList $index]
	incr index
	#Blue
	set normalizedBlueValue [lindex $imagePixelList $index]
	#先处理纯白/灰色（R=G=B）
	if {($normalizedRedValue == $normalizedGreenValue) && ($normalizedRedValue == $normalizedBlueValue)} {
		#纯白/灰颜色认为是Jx=0
		return 0
	}
	
	#接下来分别处理像素的两种颜色：G=B!=R对应正的电流密度，R=G!=B对应负的电流密度
	if {($normalizedRedValue == $normalizedGreenValue) && ($normalizedRedValue != $normalizedBlueValue)} {
		#进一步精确颜色分量的范围，R和G的范围在0.43到1之间，对于近似灰色的像素（R,G,B差别不大(差值<0.039)）则认为是Jx=0
		if {($normalizedRedValue >= 0.43) && ($normalizedBlueValue - $normalizedRedValue >= 0.039)} {
			#Jx为负值，按照颜色是线性变化的，来计算对应的电流密度的大小
			#Jx负极值是-3.5e12，对应的R+G+B=0.43+0.43+1=1.86，而Jx=0对应的R+G+B=3
			set maxColorDiff [expr {3 - 1.86}]
			set Jx_minus [expr { (3 - ($normalizedRedValue + $normalizedGreenValue + $normalizedBlueValue)) * (-3.5e12 / $maxColorDiff) * $Jx_COLOR_OPERATOR_VALUE}]
			return $Jx_minus
		} else {
		#不在范围的颜色分量认为是Jx=0
		return 0
		}
	}
	
	if {($normalizedBlueValue == $normalizedGreenValue) && ($normalizedRedValue != $normalizedBlueValue)} {
		#进一步精确颜色分量的范围，G和B的范围在0.52到1之间，此处根据模拟结果稍微增加了范围，对于近似灰色的像素（R,G,B差别不大(差值<0.039)）则认为是Jx=0
		if {($normalizedGreenValue >= 0.43) && ($normalizedRedValue - $normalizedGreenValue >= 0.039)} {
			#Jx为正值
			#Jx正极值是3e12，对应的R+G+B=1+0.52+0.52=2.04，而Jx=0，对应的R+G+B=3
			set maxColorDiff [expr {3 - 2.04}]
			set Jx_plus [expr {(3 - ($normalizedRedValue + $normalizedGreenValue + $normalizedBlueValue)) * (3e12 / $maxColorDiff) * $Jx_COLOR_OPERATOR_VALUE}]
			return $Jx_plus
		} else {
		#不在范围的颜色分量认为是Jx=0
		return 0
		}
	}
	
	##其余的颜色分量认为是Jx=0
	return 0
}
###########不均匀分布的电流密度设置###########

###########不均匀的电流极化方向设置###########
Specify Oxs_ScriptVectorField:electricPolarization {
	script setRegionPolarization
	script_args rawpt
	norm 1
	atlas :atlas
}

proc setRegionPolarization { x y z } {
	global Y_model_y
	#使用MIF2.2的命令获取当前单元格所在的区域
	set positionRegion [GetAtlasRegionByPosition :atlas $x $y $z]
	#判断所属区域
	if {$positionRegion == "baseRegion"} {
	return [list 0 -1 0]
	}
	if {$positionRegion == "topArmRegion"} {
	return [list 0.707 -0.707 0]
	}
	if {$positionRegion == "bottomArmRegion"} {
	return [list -0.707 -0.707 0]
	}
	if {$positionRegion == "topArcRegion"} {
	#上圆环的圆心坐标（333像素,200像素）,注意图像的y像素转化到模型的真实坐标需要变换（注意结果矢量的方向！）
	set vectorDirection_x [expr {$x - 333e-9}]
	set vectorDirection_y [expr {$y - ($Y_model_y - 200e-9)}]
	return [list $vectorDirection_x $vectorDirection_y 0]
	}
	if {$positionRegion == "bottomArcRegion"} {
	#下圆环的圆心坐标（333像素,500像素）
	set vectorDirection_x [expr {333e-9 - $x}]
	set vectorDirection_y [expr {($Y_model_y - 500e-9) - $y}]
	return [list $vectorDirection_x $vectorDirection_y 0]
	}
	#其他没有定义的区域
	return [list 0 -1 0]
}
###########不均匀的电流极化方向设置###########

#定义时间演化器，设置SOT的作用效果
#对比文章中SHE的类阻尼项和模拟中的Oxs_SpinXferEvolve的类阻尼项可得：
#1.在模拟中要消除(m·mp),即Lambda=1
#2.Oxs_SpinXferEvolve中的P等于(+1)*自旋霍尔角
#文章中通过Rashba效应的类场项是通过与SHE的类阻尼项之间的比值关系来设置的
#在模拟中，类场项/类阻尼项=eps_prime/(P/2)，如比值为0.5,则eps_prime为0.0325
Specify Oxs_SpinXferEvolve:evolver [subst {
	comment "定义阻尼系数"
	alpha 0.02
	J :currentDensity
	mp :electricPolarization
	P 0.13
	Lambda 1
	eps_prime 0
}]

#定义驱动器
Specify Oxs_TimeDriver [subst {
	evolver :evolver
	mesh :mesh
	comment "设置一个阶段的停止时间"
	stopping_time $stage_time
	comment "设置模拟包含的阶段数量"
	stage_count $number_of_stages
	comment "不在Y型之内的区域的饱和磁化强度为0"
	Ms {Oxs_AtlasScalarField {
	atlas :atlas
	values {
	baseRegion $Ms
	topArcRegion $Ms
	bottomArcRegion $Ms
	topArmRegion $Ms
	bottomArmRegion $Ms
	no_magneticRegion 0
	}
	}}
	m0 { Oxs_FileVectorField {
    file "SeedDomain@PadA.omf"
	multiplier 1.0
	atlas :atlas
	}
	}
	comment "将checkpoint_interval设为-1，从而禁用检查点功能"
    checkpoint_interval  -1
}]
###########时间演化的相关参数设置###########

#每个阶段固定为10ps，模拟总共运行6ns，应该生成600个磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206
  • 207
  • 208
  • 209
  • 210
  • 211
  • 212
  • 213
  • 214
  • 215
  • 216
  • 217
  • 218
  • 219
  • 220
  • 221
  • 222
  • 223
  • 224
  • 225
  • 226
  • 227
  • 228
  • 229
  • 230
  • 231
  • 232
  • 233
  • 234
  • 235
  • 236
  • 237
  • 238
  • 239
  • 240
  • 241
  • 242
  • 243
  • 244
  • 245
  • 246
  • 247
  • 248
  • 249
  • 250
  • 251
  • 252
  • 253
  • 254
  • 255
  • 256
  • 257
  • 258
  • 259
  • 260
  • 261
  • 262
  • 263
  • 264
  • 265
  • 266
  • 267
  • 268
  • 269
  • 270
  • 271
  • 272
  • 273
  • 274
  • 275
  • 276
  • 277
  • 278
  • 279
  • 280
  • 281
  • 282
  • 283
  • 284
  • 285
  • 286
  • 287
  • 288
  • 289
  • 290
  • 291
  • 292
  • 293
  • 294
  • 295
  • 296
  • 297
  • 298
  • 299
  • 300

以上代码只有三处需要注意：
①在定义DMI能的时候，我们都知道由于DMI，所以磁体系就有了手性，原文中IDMI强度D=2.0mJ/m2时，畴壁内的磁矩方向为+z指向-z。但是经过模拟发现：当把代码中D设为2.0时，畴壁内的磁矩方向为-z指向+z，当把代码中D设为-2.0时，畴壁内的磁矩方向为+z指向-z，其实回头看笔记03的稳态畴壁，也是同样的现象，因此我在代码中改变了D的正负来保持和原文中的原理图像中磁矩方向一致。
②在把电流密度的图像映射为具体的电流密度数值时，定义了Jx_COLOR_OPERATOR_VALUE变量，此处它的值暂时为-1，负号的原因在上文已经解释过了，此处关于它的映射比例尺需要注意，待会会改变这个比例尺，原因见后文。
③该mif文件的开头声明了使用的MIF2.0格式，这是因为代码中使用了GetAtlasRegionByPosition命令，所以相应的，必须使用SetOptions命令设置输出数据的格式，而不是在驱动器中指定。同时大家在写代码时也要注意一些MIF2.0格式特有的代码格式。

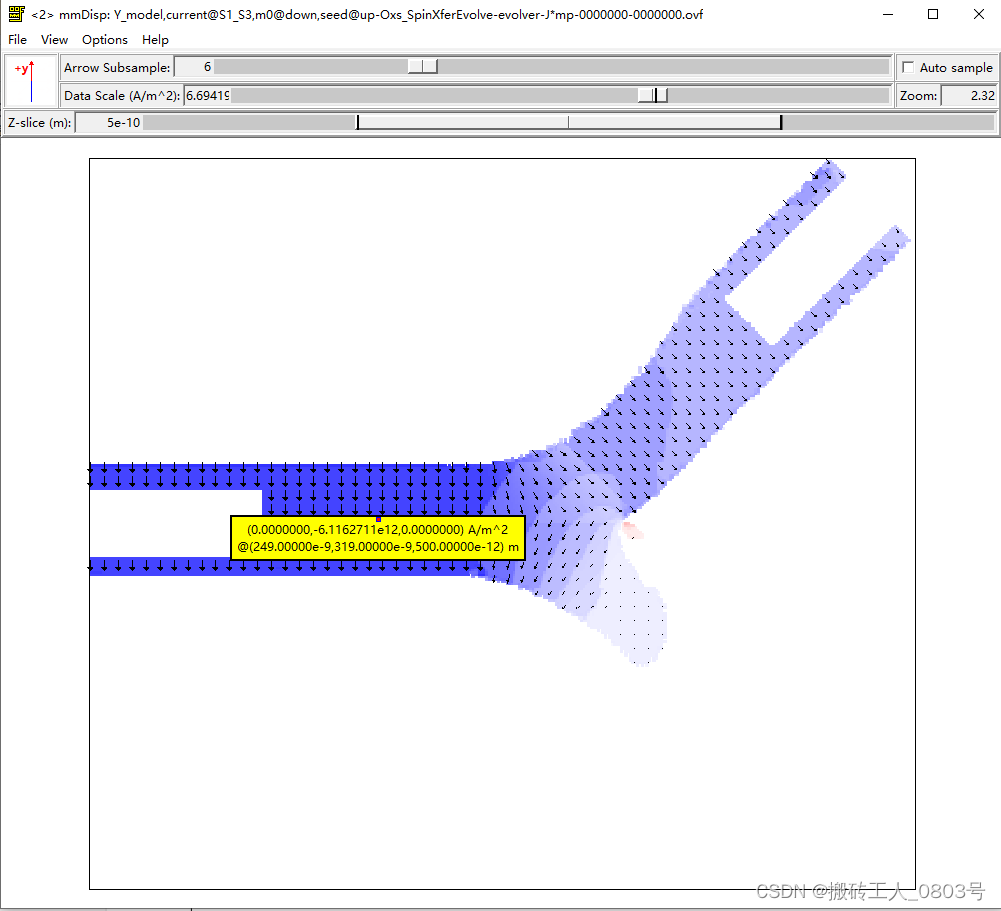
为了检验代码中电流密度和电子极化方向的正确与否，将Oxs_SpinXferEvolve类的矢量场J*mp输出显示如下：

在这里插入图片描述
可以看到无论是电流密度的大小还是电子的极化方向都是和原文大致相同的，这说明使用的模拟代码是没有多大的问题的。

模拟结束后，将生成的600个磁化文件转化为图片之后，再制作成SOT驱动SDW的动画（每张图间隔0.5s）如下：
在这里插入图片描述
观察到畴壁移动到盘A与臂的交界位置就不动了，我暂时不晓得驱动失败的原因，不过我尝试修改多个参数（包括P的正负和大小，D的正负和大小，eps_prime的正负和大小，以及Jx_COLOR_OPERATOR_VALUE的正负和大小）后，经过一通瞎折腾后，发现只有参数P和参数Jx_COLOR_OPERATOR_VALUE会影响是否生成SDW，不过参数P代表的自旋霍尔角是根据重金属材料的种类而固定的，所以本着“畴壁不动就加大电流”的理念，在代码中做出了如下修改：

set Jx_COLOR_OPERATOR_VALUE -2

  • 1

这里将电流密度设为了原来的两倍，其实经过模拟测试，这个倍数关系是有一定的范围的，若小于这个范围，则出现上图那样不能驱动畴壁移动，若大于这个范围，则整个磁体系变成混乱的状态了。那么增大后的电流密度和电子极化方向的分布就变成了这样：

在这里插入图片描述
增大电流模拟结束后，生成SDW的过程如下：
在这里插入图片描述
将模拟结束后得到的包含SDW的磁化文件命名为“SDW.omf”，作为后面测试弛豫模拟的初始磁化文件。
除此之外，也模拟了Jx_COLOR_OPERATOR_VALUE = -2，eps_prime等于0.0325和-0.0325时SDW的生成过程分别如下所示：
在这里插入图片描述
在这里插入图片描述

四、 FIG.3

FIG.3表示的是测试使用相反的初始磁化状态是否能生成SDW，那么在FIG.2(c-f)代码的基础上，只需修改时间驱动器中的一行代码即可：

multiplier -1.0

  • 1

这样就把磁化文件中的所有磁矩反向了，那么使用这个反向的磁化状态作为模拟的初始状态，得到的模拟结果如下所示：
在这里插入图片描述
果然是混乱状态，不能生成SDW，和原文描述一致。

五、 FIG.5

FIG.5表示需要在不同的DMI强度下，弛豫前面生成的SDW，由于与时间无关，所以此处选用能量最小化演化器和驱动器，当模拟自动停止的时候，就表示磁体系已经到达了稳态。当D=0时，所使用的的弛豫代码如下：

# MIF 2.2

#################
#author:YQYUN
#date:22/5/20
#desc:使用图片生成的Y型FM单层体系
#desc:这个文件专门用于弛豫模拟结束后的Y型磁体系
#################

set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]

#指定待弛豫的.omf文件名称
set fileName "SDW.omf"

#指定输出数据的格式和精度
SetOptions {
	comment "将矢量场输出的数据格式设置为ASCII文本格式（默认为b8格式）"
	vector_field_output_format {text %#.17g}
}

#容纳Y型磁体系的容器尺寸：712*630*1nm
Parameter Y_model_x 712
Parameter Y_model_y 630
Parameter Y_model_z 1
set Y_model_x [expr {$Y_model_x*1e-9}]
set Y_model_y [expr {$Y_model_y*1e-9}]
set Y_model_z [expr {$Y_model_z*1e-9}]

#单元格尺寸：2*2*1nm（单元格尺寸小于交换长度Lex=8.4nm）
Parameter xcell 2
Parameter ycell 2
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]

#定义纳米线形状，按照DMI示例文件中的形式，需要使用Oxs_MultiAtlas类来定义容器
Specify Oxs_MultiAtlas:atlas [subst { 
	atlas { Oxs_ImageAtlas:world { 
	xrange {0 $Y_model_x}
	yrange {0 $Y_model_y}
	zrange {0 $Y_model_z}
	image Y_model.png
	viewplane "xy"
	comment "依次是：左边基础区域，上圆弧区域，下圆弧区域，右边上臂区域，右边下臂区域，无磁性的区域"
	colormap {
	#FF0000 baseRegion
	#FFF200 topArcRegion
	#FF00FF bottomArcRegion
	#00FF00 topArmRegion
	#0000FF bottomArmRegion
	default no_magneticRegion
	}
	matcherror 0.2
}}
}]

#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
	cellsize {$xcell $ycell $zcell}
	atlas :atlas
}]

#定义交换能（15pJ/m）
Specify Oxs_UniformExchange {
	A 15e-12
}

#定义单轴各向异性能（垂直方向，0.8MJ/m3）
Specify Oxs_UniaxialAnisotropy {
	K1 0.8e6
	axis {0 0 1}
}

#定义退磁能
Specify Oxs_Demag {}

#定义DMI能
set D 0
#根据文章中所说的畴壁中磁矩指向为正指向负，对应在此代码中则将D改变符号
set D [expr {$D * -1}]
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
	default_D $DD
	atlas :atlas
	comment "按区域分配DMI系数"
	D {
	baseRegion baseRegion $DD
	topArcRegion topArcRegion $DD
	bottomArcRegion bottomArcRegion $DD
	topArmRegion topArmRegion $DD
	bottomArmRegion bottomArmRegion $DD
	no_magneticRegion no_magneticRegion 0
	}
}]

#定义饱和磁化强度Ms（580kA/m）
set Ms 5.8e5

#使用能量最小化演化器弛豫
Specify Oxs_CGEvolve:evolver {}

#使用最小化驱动器快速推进到稳态
Specify Oxs_MinDriver [subst {
	evolver :evolver
	mesh :mesh
	stopping_mxHxm 0.1
	comment "不在Y型之内的区域的饱和磁化强度为0"
	Ms {Oxs_AtlasScalarField {
	atlas :atlas
	values {
	baseRegion $Ms
	topArcRegion $Ms
	bottomArcRegion $Ms
	topArmRegion $Ms
	bottomArmRegion $Ms
	no_magneticRegion 0
	}
	}}
	m0 {Oxs_FileVectorField {
    file $fileName
	atlas :atlas
	}
	}
}]

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126

那么当D=0时，整个弛豫过程如下：
在这里插入图片描述
可以看到最后的稳态和原文FIG.5(a)有差异，不过模拟结果是符合原文的描述的：SDW转化为多畴。
当D=1时，整个弛豫过程如下：
在这里插入图片描述
原文中说D=1时SDW会消失，从而磁体系变成单畴状态。但是此处的模拟结果居然和D=0时差不多，额，，我搞不懂这是什么原因导致的呢？
当D分别等于1.5，2，3时，弛豫过程分别如下：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
可以看到当D去这三个值时，模拟结果得到的最终的稳态和原文描述的差不多。将D=2时，把得到的稳态磁化文件命名为“SDW_Relaxed_D@2.omf”并作为后面测试自旋波传播模拟的初始磁化。
当D等于4时，弛豫过程如下：
在这里插入图片描述
虽然模拟得到的最终的稳态和原文不太一样，但是此处的模拟结果也符合原文描述：SDW变成了labyrinthine wormlike结构。

六、 FIG.6(a),(d)

首先声明一点，原文FIG.6(a)采用的是“60°Y型”磁体系，而此处使用的是“90°Y型”磁体系来进行模拟。
和笔记03采用带状天线激发自旋波的方式相同，从 FIG.6中通过像素转换关系找到带状天线的位置在x方向[196nm,207nm]宽度共计11nm，至于y方向的范围则是至少跨越整个基底的宽度。由于原文中只说了自旋波的频率为30GHz，没有说激发自旋波的外加磁场的形式，所以此处暂且使用200Oe，30GHz的sin和sinc两种函数形式在x方向变化的外加磁场来激发自旋波，从图(d)中可看出需要分析的截止频率为80GHz，所以将保存磁化文件的时间间隔设置为6ps，使采样频率稍微大于截止频率的两倍。模拟时间则假设为3ns。
通过带状天线激发的自旋波会沿着SDW传播，正如原文图中红框包围的区域，选择用于进行一维FFT分析的采样区域为：
上臂的采样区域：
x_start, x_end = 493e-9,495e-9
y_start, y_end = 343e-9,489e-9
z_start, z_end = 0,1e-9
下臂的采样区域：
x_start, x_end = 493e-9,495e-9
y_start, y_end = 147e-9,289e-9
z_start, z_end = 0,1e-9

综上，使用sin形式的外加磁场的模拟代码如下：

# MIF 2.2

#################
#author:YQYUN
#date:22/5/20
#desc:Y型FM（下层）/HM（上层）双层磁体系
#desc:基于条带状天线(x方向位置：196nm到207nm)激发自旋波，外加磁场为x方向：H=200Oe * sin(2 * pi * 30GHz * t)
#################

set pi [expr {4*atan(1.0)}]
set mu0 [expr {4*$pi*1e-7}]

#使用时间驱动器的总共运行时间为3e-9s
Parameter run_time  3e-9
#每个阶段6e-12s
Parameter stage_time  6e-12
set number_of_stages [expr {int(ceil($run_time/double($stage_time)))}]

#指定输出数据的格式和精度
SetOptions {
	comment "将矢量场输出的数据格式设置为ASCII文本格式（默认为b8格式）"
	vector_field_output_format {text %#.17g}
}

#容纳Y型磁体系的容器尺寸：712*630*1nm
Parameter Y_model_x 712
Parameter Y_model_y 630
Parameter Y_model_z 1
set Y_model_x [expr {$Y_model_x*1e-9}]
set Y_model_y [expr {$Y_model_y*1e-9}]
set Y_model_z [expr {$Y_model_z*1e-9}]

#单元格尺寸：2*2*1nm（单元格尺寸小于交换长度Lex=8.4nm）
Parameter xcell 2
Parameter ycell 2
Parameter zcell 1
set xcell [expr {$xcell*1e-9}]
set ycell [expr {$ycell*1e-9}]
set zcell [expr {$zcell*1e-9}]

#定义纳米线形状，按照DMI示例文件中的形式，需要使用Oxs_MultiAtlas类来定义容器
Specify Oxs_MultiAtlas:atlas [subst {
	atlas { Oxs_ImageAtlas:world {
	xrange {0 $Y_model_x}
	yrange {0 $Y_model_y}
	zrange {0 $Y_model_z}
	image Y_model.png
	viewplane "xy"
	comment "依次是：左边基础区域，上圆弧区域，下圆弧区域，右边上臂区域，右边下臂区域，无磁性的区域"
	colormap {
	#FF0000 baseRegion
	#FFF200 topArcRegion
	#FF00FF bottomArcRegion
	#00FF00 topArmRegion
	#0000FF bottomArmRegion
	default no_magneticRegion
	}
	matcherror 0.2
}}
}]

#定义网格尺寸
Specify Oxs_RectangularMesh:mesh [subst {
	cellsize {$xcell $ycell $zcell}
	atlas :atlas
}]

#定义交换能（15pJ/m）
Specify Oxs_UniformExchange {
	A 15e-12
}

#定义单轴各向异性能（垂直方向，0.8MJ/m3）
Specify Oxs_UniaxialAnisotropy {
	K1 0.8e6
	axis {0 0 1}
}

#定义退磁能
Specify Oxs_Demag {}

#定义DMI能（文中IDMI强度为2.0mJ/m2）
set D 2.0
#根据文章中所说的畴壁中磁矩指向为正指向负，对应在此代码中则将D改变符号
set D [expr {$D * -1}]
set DD [expr {$D/1000}]
Specify Oxs_DMExchange6Ngbr:DMEx [subst {
	default_D $DD
	atlas :atlas
	comment "按区域分配DMI系数"
	D {
	baseRegion baseRegion $DD
	topArcRegion topArcRegion $DD
	bottomArcRegion bottomArcRegion $DD
	topArmRegion topArmRegion $DD
	bottomArmRegion bottomArmRegion $DD
	no_magneticRegion no_magneticRegion 0
	}
}]

#定义饱和磁化强度Ms（580kA/m）
set Ms 5.8e5

###########施加用于激发自旋波的sin形式的外加磁场###########

#sin形式的外加磁场的振幅，这里的单位为mT
set Happ 20

#sin形式的外加磁场的频率，这里的单位为GHz
set frequency 30

#对初始的矢量场appliedFiled进行变化，
#使其成为外加磁场（+x方向）：H=200Oe * sin(2 * pi * 30GHz * t)
proc transformExcitationFiled { total_time } {
	global frequency pi
	set t $total_time
	#计算w=2*pi*f，并把单位顺便转化为GHz
	set w [expr {2 * $pi * $frequency * 1e9}]
	set sinwt [expr {sin($w * $t)}]
    set coswt [expr {cos($w * $t)}]
	#计算x方向的磁场分量及其对时间的导数
	#即x方向Hx*sinwt
	set Hx $sinwt
	set dHx [expr {$w * $coswt}]
	#其余两个方向都为0
	#返回6个元素的列表，即变换矩阵的3个主对角元素及其3个导数
	return [list $Hx 0 0 $dHx 0 0]
}

#指定施加外加磁场的区域（后面转化为磁场），即x方向位置：196nm到207nm：H=(Happ 0 0)，其他区域H=(0 0 0)
proc setAppliedFiled { x y z } {
	global Happ
	if {$x >= 196e-9 && $x <= 207e-9} {
	return [list $Happ 0 0]
	} else {
	#其他区域无外加磁场
	return [list 0 0 0]
	}
}
#使用脚本指定外加磁场的区域的矢量场
Specify Oxs_ScriptVectorField:appliedFiled {
	script setAppliedFiled
	script_args rawpt
	atlas :atlas
}

#使用此类可生成任意（局域，时变）的外加磁场
Specify Oxs_TransformZeeman [subst {
    field :appliedFiled
	comment "函数返回6个元素，是3个主对角元素及其3个导数"
	type diagonal
	script transformExcitationFiled
	script_args total_time
	comment "将默认单位A/m换算为mT"
	multiplier [expr {0.001/$mu0}]
	comment "将stage_count设为0（默认值），让模拟的所有阶段都存在该塞曼能"
	stage_count 0
}]
###########施加用于激发自旋波的sin形式的外加磁场###########

###########时间演化的相关参数设置###########

#定义演化器（龙格-库塔时间演化器）
Specify Oxs_RungeKuttaEvolve:evolver {
	comment "阻尼系数0.02"
	alpha 0.02
}

#定义驱动器
Specify Oxs_TimeDriver [subst {
	evolver :evolver
	mesh :mesh
	comment "设置一个阶段的停止时间"
	stopping_time $stage_time
	comment "设置模拟包含的阶段数量"
	stage_count $number_of_stages
	comment "Y型区域之外的区域的饱和磁化强度为0"
	Ms {Oxs_AtlasScalarField {
	atlas :atlas
	values {
	baseRegion $Ms
	topArcRegion $Ms
	bottomArcRegion $Ms
	topArmRegion $Ms
	bottomArmRegion $Ms
	no_magneticRegion 0
	}
	}}
	comment "将D=2时弛豫后的磁化文件作为初始磁化"
	m0 { Oxs_FileVectorField {
    file "SDW_Relaxed_D@2.omf"
	multiplier 1.0
	atlas :atlas
	}
	}
	comment "将checkpoint_interval设为-1，从而禁用检查点功能"
    checkpoint_interval  -1
}]
###########时间演化的相关参数设置###########

#每个阶段固定为6ps，模拟总共运行3ns，应该生成500个磁化文件
Destination Record mmArchive
Schedule Oxs_TimeDriver::Magnetization Record stage 1


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204

FIG.6(a)是自旋波传播的空间分布图，图中用颜色代表自旋波的振幅，这种图像是使用semargl3软件生成的，但我暂时还不会用，所以我也不会生成图(a)这样的图片，不过根据关系式m(x,y,z,t)=m基态(x,y,z)+m自旋波(x,y,z,t)，用当前时刻的磁化状态m(x,y,z,t0)减去基态磁化（即初始磁化状态）m基态(x,y,z)就可以得到自旋波随时间的传播。
利用oommf的命令行工具avfdiff可以得到两个矢量场文件的差值，但是该工具不支持指定文件目录，故一次只能生成一条命令运行，不过可以使用批处理命令批量生成所需的命令，批处理命令如下：

@ rem 请将该批处理文件放在oommf安装根目录

@ rem 注意待处理的磁化文件相对于本文件的位置
@ set inFileFilter=TODO_picture\矢量图处理\*.*f

@ rem 以下命令是使用avfdiff的命令，请先理解它的命令参数
@ rem %%i是输入omf文件的名称
for %%i in (%inFileFilter%) do (
tclsh oommf.tcl avfdiff ^
TODO_picture\矢量图处理\SDW_Relaxed_D@2.omf ^
%%i
)

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12

将生成的矢量场差值文件转化为图片(颜色表示mx的大小)，再制作成动画如下所示：

sin自旋波的传播过程

用颜色代表mz的大小，得到的动画如下：

sin自旋波(mz)

基于上面的代码，将它修改成使用sinc形式的外加磁场的部分模拟代码如下：

#sinc形式的外加磁场的振幅，这里的单位为mT
set Happ 20

#sinc形式的外加磁场的频率，这里的单位为GHz
set frequency 30

#t0=1e-15s
set t0 1e-15

#对初始的矢量场appliedFiled进行变化，
#使其成为外加磁场（+x方向）：H=200Oe * sinc(2 * pi * 30GHz * (t+t0))
proc transformExcitationFiled { total_time } {
	global frequency pi t0
	set t [expr {$total_time + $t0}]
	#计算w=2*pi*f，并把单位顺便转化为GHz
	set w [expr {2 * $pi * $frequency * 1e9}]
	set sinwt [expr {sin($w * $t)}]
    set coswt [expr {cos($w * $t)}]
	#计算x方向的磁场分量及其对时间的导数，其他方向为0
	#即x方向H*sincwt
	set Hx [expr {$sinwt / ($w * $t)}]
	set dHx [expr {($w * $t * $coswt - $sinwt) / ($w * $t * $t)}]
	#返回6个元素的列表，即变换矩阵的3个主对角元素及其3个导数
	return [list $Hx 0 0 $dHx 0 0]
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25

和上文同样的处理方式，用颜色表示mx的大小，生成的动画如下：

sinc自旋波传播过程

对于FIG.6(d)中的一维FFT分析，同样使用笔记03介绍的MFA程序包进行处理，得到“Y型”磁体系的上臂采样区域的幅频关系如下：
①当采用sin形式的外加磁场时：
在这里插入图片描述
②当采用sinc形式的外加磁场时：
在这里插入图片描述
“Y型”磁体系的下臂采样区域的幅频关系如下：
①当采用sin形式的外加磁场时：
在这里插入图片描述

②当采用sinc形式的外加磁场时：
在这里插入图片描述
对于得到的一维FFT结果我只想叹一声气，也没什么可以分析的。
在这里插入图片描述
说实话，我现在还是不会计算自旋波的一维和二维FFT，而别人的程序包又不好用，现在真是急得跺脚，真希望在写下一篇笔记前能学会这种计算方法。

22/8/17纠错更新：

结合笔记05正文的傅里叶变换技巧，和笔记03评论区中关于利用avfdiff获取动态磁化文件和avf2ovf来批量转换矢量场文件的数据格式的补充说明：

问题描述：原文中通过按名称升序的方式遍历输入文件夹中的每一个矢量场文件，但是通过原文中的方式来定义输出文件名（即构造outFileFullName变量）的时候需要注意：输出文件名中追加的“数字”为文本格式，而非真正的数字，所以当所有文件转化完成后，比如依次生成了100个文件：m_0.ovf，m_1.ovf，m_2.ovf，，，m_99.ovf，看起来是按照升序依次排列的，但实际上它们的名称升序顺序为：m_0.ovf，m_1.ovf，m_10.ovf，m_11.ovf，，，m_19.ovf，m_2.ovf，m_20.ovf，，，m_29.ovf，m_3.ovf，，，最简单的检验方法就是利用mmDisp的File->Open功能来浏览这些文件，来查看它们的排列顺序。
问题导致的后果：这种自定义输出文件名的数字导致了这些文件没有按常规的顺序排列，这在读取这些磁化文件做傅里叶变化时会出现错误（不是按照采样时间升序排列的）。
问题解决：最简单的方式就是不自定义输出文件名，而是和输入文件名相同，这样就相当于将转化后的矢量场文件直接替换原来的矢量场文件。这种批处理的命令如下：
@ rem 请将该批处理文件放在oommf安装根目录，并修改后缀名为.bat
@ rem 开启变量延迟
@ setlocal enabledelayedexpansion
@ rem 注意待处理的磁化文件相对于本文件的位置
@ set inFileFilter=矢量场文件夹全路径*.omf
@ rem 输出文件的名称与输入文件名称相同，否侧会打乱文件顺序
@ rem %%i是输入omf文件的名称
@ rem 以下命令是使用avf2ovf的命令，请先理解它的命令参数
for %%i in (%inFileFilter%) do (
start /min cmd /c “tclsh oommf.tcl avf2ovf -dataformat text -fileformat ovf 2 %%i %%i”
)

如今发现当时模拟不仅激发所用的sinc外加场的频率和振幅错了，而且用作傅里叶变换的动态磁化文件的顺序也错了！唉，这里就不重新模拟了，今天就只把本文最后的内容按照正确的文件顺序重新做一下一维FFT，结果如下：

“Y型”磁体系的上臂采样区域的幅频关系如下：

①当采用sin形式的外加磁场时：
在这里插入图片描述
从频谱图中可以看到30GHz的频率贡献最多，因为我们施加的就是30GHz的sin外加场。

②当采用sinc形式的外加磁场时：

在这里插入图片描述
由于模拟时sinc外加磁场的截止频率只设置了30GHz，所以频谱图也只能看30GHz以前的。

“Y型”磁体系的下臂采样区域的幅频关系如下：

①当采用sin形式的外加磁场时：

在这里插入图片描述

②当采用sinc形式的外加磁场时：

在这里插入图片描述

总结

由于原文的内容实在是太多了，所以本笔记只选择了以上内容复现。如果你觉得本系列的笔记对你有帮助，请点个赞吧！最后还是那句话：早点毕业！
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/凡人多烦事01/article/detail/359270
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号