热门标签
热门文章
- 1FPGA实现SPI接口(1)--什么是SPI接口?_fpga spi
- 2adb install 时 日志输出Performing Streamed Instal 一直卡着不动,处理方法_performing streamed install
- 3论文笔记:Does Writing with Language Models Reduce Content Diversity?
- 4华为OD机试(B+C+D卷)、机考必刷 200 分的题目整理如下,冲满分评级必备_华为od考试
- 5Gitea--优秀的轻量级代码托管平台
- 6打造类ChatGPT服务,本地部署大语言模型(LLM),如何远程访问?_langchain chatchat 公网访问
- 7LeetCode #1 两数之和_class solution { public: vector
twosum(vector - 8linux解压gz文件的命令
- 9返利网拼团小程序,10人拼团7人返利_拼团返利源码
- 10怎么购买gpt4 plus
当前位置: article > 正文
欧拉角及相关概念
作者:凡人多烦事01 | 2024-04-11 09:57:23
赞
踩
欧拉角
欧拉角定义
欧拉角表示的是刚体的姿态变换。空间中的任意一点都可以用该点到对应坐标轴的垂直距离组成的三维向量描述,同理对某个物体的姿态,也可以用三个角度表示,三个角度分别为围绕对应坐标轴(x,y,z)旋转的度数,这三个角度就是欧拉角。分别叫做翻滚角(Roll),俯仰角(Pitch)和航向角(Yaw)。
(1)翻滚角(Roll)
翻滚角α表示刚体绕坐标系x轴旋转的角度,在空间运动中,刚体围绕坐标系x轴旋转α度,姿态变换矩阵可以由翻滚角α表示:
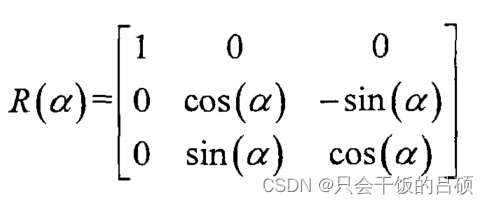
(2)俯仰角(Pitch)
俯仰角β表示刚体绕坐标系y轴旋转的角度,在空间运动中,刚体围绕坐标系y轴旋转β度,姿态变换矩阵可以由俯仰角β表示:
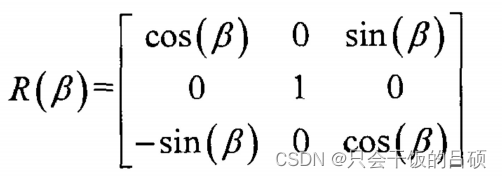
(3)航向角(Yaw)
航向角n表示刚体绕坐标系z轴旋转的角度,在空间运动中,刚体围绕坐标系z轴旋转n度,姿态变换矩阵可以由航向角n表示
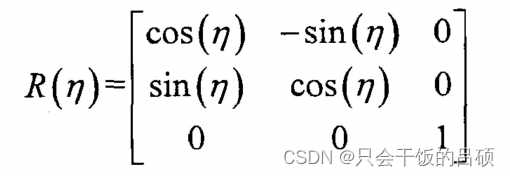
可以验证欧拉角得出的旋转矩阵满足刚体变换的要求,旋转矩阵的行列式为1以及旋转矩阵是正交矩阵。
因此可以从欧拉角得到旋转矩阵,将欧拉角表示的旋转矩阵按照一定的顺序相乘即可得到旋转变换(姿态变换矩阵),按照Z→Y →X的旋转顺序可以得到对应的旋转矩阵:
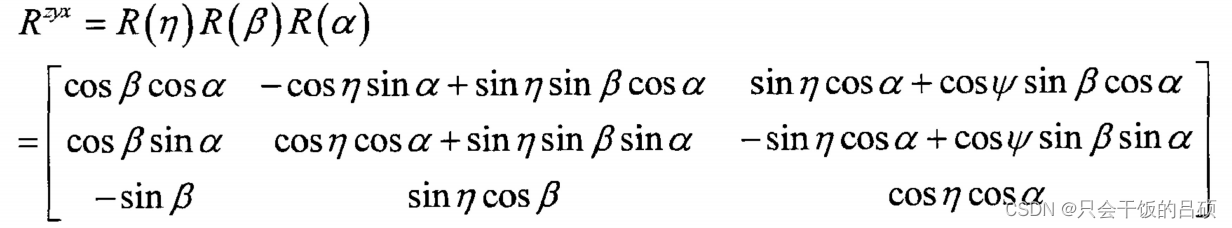
这种变化方式可以看作:三维空间向量p1,经过三次旋转后,变为p2,三次旋转依次按照z轴,y轴,x轴旋转n度,β度和α度。对应的旋转矩阵依次是欧拉角对应的旋转矩阵,用R(α),R(β),R(n)表示,同时三维空间向量p1,也可以看作一次旋转,直接变为向量p2,那么可以得出:
![]()
另外,也可以根据旋转矩阵,求解对应的欧拉角:
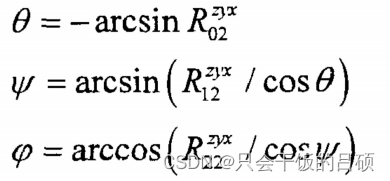
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/凡人多烦事01/article/detail/404289
推荐阅读
相关标签



