力扣爆刷第105天之CodeTop100五连刷11-15

力扣爆刷第105天之CodeTop100五连刷11-15

一、5. 最长回文子串

题目链接：https://leetcode.cn/problems/longest-palindromic-substring/description/
思路：求最长回文子串，要以单点为中心或以双点为中心，向左右进行扩散，然后遍历字符串，在每一个点位上向两边进行扩散，然后记录即可。

class Solution {
    public String longestPalindrome(String s) {
        String max = "";
        for(int i = 0; i < s.length(); i++) {
            String s1 = find(s, i, i);
            String s2 = find(s, i, i+1);
            max = s1.length() > max.length() ? s1 : max;
            max = s2.length() > max.length() ? s2 : max;
        }
        return max;
    }

    String find(String s, int i, int j) {
        while(i >= 0 && j <= s.length()-1) {
            if(s.charAt(i) != s.charAt(j)) {
                break;
            }
            i--;
            j++;
        }
        return s.substring(i+1, j);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

二、33. 搜索旋转排序数组

题目链接：https://leetcode.cn/problems/search-in-rotated-sorted-array/description/
思路：对于二分法有几个定理。
定理一：只有在顺序区间里才能通过区间两端的值来判断target是否存在其中。
定理二：判断是顺序区间还是乱序区间，只需要看nums[left]是否小于等于nums[right]，小于等于的话即顺序，其他乱序。
定理三：每次二分都至少会确定一个顺序区间。
那么本题就可以不停的二分，然后进入其中的顺序区间，看看target是否在这段顺序区间内（通过两端数值即可判断），在的话就往其内移动指针，不在就往反方向移动指针，即可。
也就是下面说的：
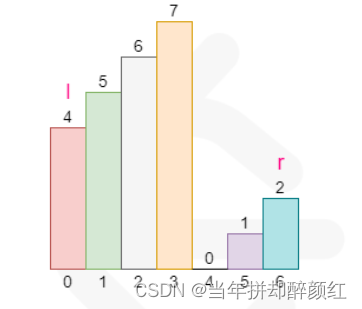
将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] == target) return mid;
            if(nums[left] <= nums[mid]) {
                if(nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                }else{
                    left = mid + 1;
                }
            }else{
                if(nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                }else{
                    right = mid - 1;
                }
            }
        }
        return -1;
    }

    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

三、102. 二叉树的层序遍历

题目链接：https://leetcode.cn/problems/binary-tree-level-order-traversal/description/
思路：层序遍历使用队列，靠队列长度表示层宽，遍历即可。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<List<Integer>> arrayList = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        if(root == null) return arrayList;
        Deque<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            for(int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left != null) {
                    queue.add(node.left);
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            arrayList.add(list);
        }
        return arrayList;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

四、200. 岛屿数量

题目链接：https://leetcode.cn/problems/number-of-islands/description/
思路：深度优先算法，是岛屿就标记为海洋，每次递归结束岛屿计数加一。

class Solution {
    
    public int numIslands(char[][] grid) {
        int count = 0;
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(grid[i][j] == '1') {
                    dfs(grid, i, j);
                    count++;
                }
            }
        }
        return count++;
    }

    void dfs(char[][] grid, int x, int y) {
        if(x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] == '0') return;
        grid[x][y] = '0';
        dfs(grid, x-1, y);
        dfs(grid, x+1, y);
        dfs(grid, x, y-1);
        dfs(grid, x, y+1); 
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

五、121. 买卖股票的最佳时机

题目链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/
思路：买卖股票是典型的动态规划题，对于这类题型，每一天有两种状态，即持有和不持有。对于持有可以是之前就持有了，也可以是今天才持有的。对于不持有可以是之前就不持有了，也可以是今天才持有的。
对于dp[i]的定义是经过第i天，所能获取的最大利润。因此我们就要对于所有的状态，进行对应的选择，动态规划就是状态与选择。

class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[2];
        dp[0] = -prices[0];
        for(int i = 1; i < prices.length; i++) {
            dp[0] = Math.max(dp[0], -prices[i]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
        }
        return dp[1];
    }
}
1
2
3
4
5
6
7
8
9
10
11

本题还可以使用贪心来做：遍历的过程中一直记录最小值，然后一直用当前值减去最小值来更新最大值。

class Solution {
    public int maxProfit(int[] prices) {
        int max = 0, min = Integer.MAX_VALUE;
        for(int i = 0; i < prices.length; i++) {
            min = Math.min(min, prices[i]);
            max = Math.max(max, prices[i] - min);
        }
        return max;
    }
}
1
2
3
4
5
6
7
8
9
10