凡人多烦事01

这个屌丝很懒，什么也没留下！

热门标签

机器学习算法——逻辑斯蒂回归_动手学机器学习6 4 动手实现逻辑斯谛回归 69

作者：凡人多烦事01 | 2024-04-24 03:36:32

踩

动手学机器学习6 4 动手实现逻辑斯谛回归 69

一、逻辑斯蒂回归算法概述

1、算法介绍

逻辑斯蒂回归（Logistic Regression）是一种用于解决分类问题的机器学习算法。它是通过将线性回归模型的输出映射到一个概率值，然后根据这个概率值进行分类的。

逻辑斯蒂回归假设因变量（要预测的变量）与自变量之间存在一个线性关系，然后使用逻辑函数（也称为sigmoid函数）将线性组合转化为概率值。

2、算法优缺点

（1）、优点：

简单而高效：逻辑斯蒂回归算法相对简单，易于理解和实现。它的计算速度快，在处理大规模数据时表现出较好的效率。
可解释性强：逻辑斯蒂回归输出的是概率值，可以直接解释为某个样本属于某个类别的概率。同时，权重参数的大小和方向可以提供关于自变量对因变量影响的有用信息。
鲁棒性强：逻辑斯蒂回归对于异常值的影响相对较小，能够处理包含噪声的数据集。
适用性广泛：逻辑斯蒂回归可以应用于各种类型的特征，包括连续型和离散型特征。此外，它也可以用于二分类问题和多分类问题。

（2）、缺点：

线性关系假设：逻辑斯蒂回归假设因变量与自变量之间存在线性关系，如果数据集中的关系非线性，逻辑斯蒂回归可能无法很好地拟合数据。
容易产生欠拟合：当特征之间存在复杂的非线性关系时，逻辑斯蒂回归的表达能力可能不足，导致欠拟合现象。
对异常值敏感：虽然逻辑斯蒂回归对于小规模的异常值比较鲁棒，但在存在大量异常值的情况下，模型的性能可能会受到影响。
数据要求独立性：逻辑斯蒂回归假设样本之间相互独立，如果数据集中存在相关性较强的样本，模型的性能可能会下降。

二、逻辑斯蒂算法原理

在理解逻辑斯蒂算法之前，我们先来了解一下线性模型与回归

1、线性模型与回归

在二维平面上，线性模型一般是 $y=kx+b$ 这样的形式来出现，但是在实际情况中，输入的样本 $x$ 一般都会有不止一个特征，因此一般情况下的线性模型如下：

$f ( x )= w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d} + b$

其中 $x=(x_{1}, x_{2}, ..., x_{d})$ 是由d维属性描述的样本，其中 $x_{i}$ 是 x 在第 i 个属性上的取值。w则是各个x对应的参数。当然这样子书写仍是会过于麻烦，所以一般以向量的形式表示：

$f ( x )= w^{T } x + b$

其中 $w=(w_{1}, w_{2}, ..., w_{d})$ 为待求解系数；

因此，我们构造了一个线性模型，然后我们将得到的样本送进模型中进行训练，最后用训练过的线性模型来尽可能准确地预测实值输出标记。

2、最小二乘法

既然要训练这个线性回归模型，那么每次训练的参数w和b的求解就很重要，参数w和b的求解我们使用的是最小二乘法。

线性回归的目标是要让否 $f(x_{i})$ （预测值）尽可能的去接近 $y_{i}$ （真实值）

接下来我们以一维数据为例使用最小二乘法求解参数w和b的值：

设其回归值与实际观察之间存在的误差 $e_{i}$ ，则学习的目标为：

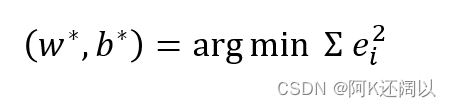
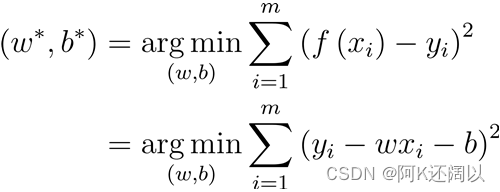
最小化均方误差：

分别对w和b求导，可得：

得到解析/闭合（closed-form）解：

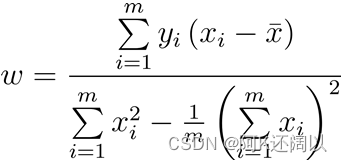
3、sigmod函数

之所以逻辑斯蒂回归会被用于分类问题而不是回归问题，其中最重要的转折点就是运用到了sigmod函数：

sigmod函数的图像：

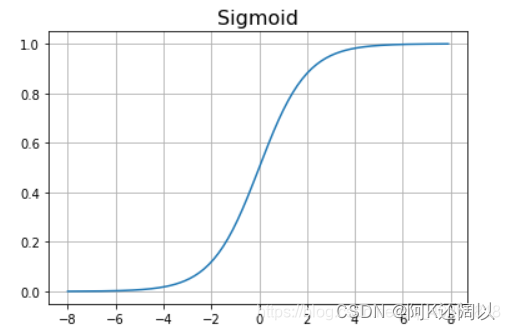
我们将回归的出来的值映射到sigmod函数当中，以此来判断样本是正还是负，来解决二分类问题。

4、极大似然估计

运用sigmod函数之后原来的线性回归模型变为：

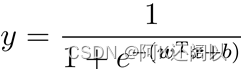
样本作为正例的相对可能性的对数：

对数几率：

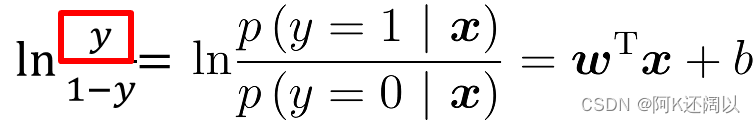
因此可以得到正样本和负样本的概率：

为了确定待求解的未知参数 $\theta$ 1 , $\theta$ 2 , . . . .，如均值、方差或特定分布函数的参数等，我们需要使用极大似然估计来求解；计算每个样本 X 1 , X 2 , . . . , X n 的概率密度 f ( Xi; $\theta$ 1, . . . , $\theta$ m) .

假定样本 i.i.d ，则可根据样本的概率密度累乘构造似然函数 :

$L(\theta _{1},.....,\theta _{m}) = \prod f (xi; \theta_{1} ,....,\theta_{m}).$

通过似然函数最大化（求导为零），求解未知参数 $\theta$ ,以下是计算过程：

假定有样本集 { X 1 , X 2 ,…, X n } 服从参数为 μ 的泊松分布，对于观测样本 X 的概率为：

假定样本之间独立同分布，则样本集的联合概率为：

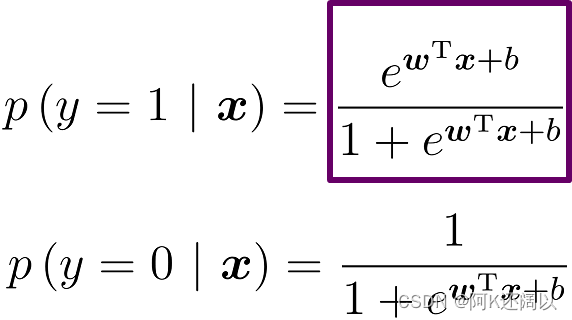
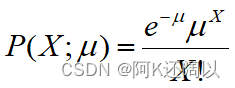
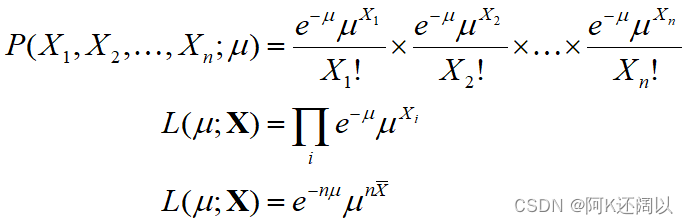
三、逻辑斯蒂算法实战

1、数据准备

本次使用的是心脏病患者数据集，下图是该数据集的一部分：

本数据集来自archive.ics.uci.edu/static/public/45/data.csvUCI机器学习仓库archive.ics.uci.edu/static/public/45/data.csv

其中各个字段代表的意思：

age: 患者的年龄。
sex: 患者的性别（一般来说，1代表男性，0代表女性）。
cp: 胸痛类型（chest pain type）。通常分为几种类型，例如典型心绞痛、非典型心绞痛、非心绞痛胸痛、无症状等。
trestbps: 静息血压（在医院入院时测量的mmHg）。
chol: 血清胆固醇含量（mg/dl）。
fbs: 空腹血糖（fasting blood sugar），如果大于120 mg/dl则标记为1（表示存在糖尿病风险），否则为0。
restecg: 静息心电图结果。可能有几种状态，如正常、ST-T波异常或左室肥大。
thalach: 达到的最大心率。
exang: 运动诱发心绞痛（exercise induced angina），1表示有，0表示无。
oldpeak: 相对于休息状态，运动引起的ST段下降（以毫米计）。
slope: ST段峰值运动后的斜率。与心脏健康有关的测量，可能有几种不同的值。
ca: 经荧光透视染色的主要血管数量（0-3）。
thal: 缺血性心脏病患者的地中海贫血测试结果。可能有几种不同的值，比如正常、固定缺陷、可逆缺陷等。
num: 诊断心脏病的结果（angiographic disease status）。其中0代表没有发现疾病，而更高的数字（例如1, 2, 3, 4）表示不同程度的心脏病。

2、数据预处理

拿到数据集之后要删除有缺失值的行，并且还要进行类别型特征编码和特征缩放，将其转换成一个二分类问题，即是否患心脏病；同时要将数据集进行划分为测试集和训练集。


# 1. 数据预处理
# 加载数据集
df = pd.read_csv('https://archive.ics.uci.edu/static/public/45/data.csv')
# 处理缺失值
df.replace('NaN', np.nan, inplace=True)
df.dropna(inplace=True)
# 类别型特征编码和特征缩放
X = df.iloc[:, :-1].values
y = df.iloc[:, -1].values
y = (y > 0).astype(int)  # 将目标变量转换为二分类问题
scaler = StandardScaler()
X = scaler.fit_transform(X)
 
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

3、逻辑斯蒂回归模型构建

本次使用sigmod函数来进行构建


# 2. 逻辑斯蒂回归模型构建
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

4、训练算法

本次实验使用的是随机梯度上升算法

初始化权重：

首先，初始化权重向量为n维零向量，其中n是特征的数量。
迭代更新权重：函数通过两层循环进行权重更新。

外层循环控制迭代次数，即整个数据集被遍历的次数。num_iter参数定义了迭代的总轮数。

内层循环遍历数据集中的每个样本。
动态学习率：

在每次迭代中，学习率alpha动态调整。随着迭代次数的增加，学习率逐渐减小，但永远不会减小到0，因为有一个常数项0.01。这样可以保证在多次迭代后仍然能够调整权重，同时随着时间的推移减少步长，帮助算法收敛。
随机选择样本：

在每次内层循环中，随机选择一个样本来更新权重。这样做可以减少周期性的波动，并且有助于跳出局部最优解。
计算预测值和误差：

使用sigmoid函数计算选定样本的预测值，然后计算预测值和实际值之间的误差。
更新权重：

根据误差、学习率和选定样本的特征值来更新权重。权重的更新是朝着减少当前样本预测误差的方向进行的。
移除已选样本索引：

一旦使用了某个样本来更新权重，就从索引列表中删除该样本的索引。这确保了在一次外层循环中每个样本只被使用一次。
返回最终的权重向量：当所有迭代完成后，函数返回最终的权重向量。


# 3. 随机梯度上升算法
def stochastic_gradient_ascent(X, y, num_iter=150):
    m, n = X.shape
    weights = np.zeros(n)
    for j in range(num_iter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            randIndex = int(np.random.uniform(0, len(dataIndex)))
            h = sigmoid(np.sum(X[randIndex]*weights))
            error = y[randIndex] - h
            weights = weights + alpha * error * X[randIndex]
            del(dataIndex[randIndex])
    return weights

5、模型训练和评估


# 4. 模型训练
weights = stochastic_gradient_ascent(X_train, y_train)
 
# 5. 模型评估
def predict(X, weights):
    prob = sigmoid(np.dot(X, weights))
    return [1 if x >= 0.5 else 0 for x in prob]
 
y_pred = predict(X_test, weights)
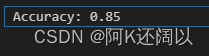
print(f'Accuracy: {accuracy_score(y_test, y_pred)}')

6、运行结果

四、实验小结

逻辑斯蒂回归是一种分类算法，尽管其名称中包含“回归”二字，但它实际上用于解决二分类问题。该算法的核心是逻辑斯蒂函数（也称为Sigmoid函数），它将任意实数映射到(0, 1)区间，可以被解释为概率。

通过学习，我掌握了如何从数学原理出发，建立逻辑斯蒂回归模型，并将其表示为一个求解参数权重的最优化问题。

学会了如何使用对数似然函数作为损失函数，并通过最大化对数似然函数来训练模型。

理解了梯度下降算法的工作原理及其在逻辑斯蒂回归中的应用，即通过迭代地更新权重来最小化损失函数。学习了随机梯度上升算法，这是梯度下降算法的一个变体，它每次更新权重时只使用一个样本，这样可以加快计算速度并处理大规模数据集。

掌握了数据预处理的重要性，包括处理缺失值、特征编码、特征缩放等，这些步骤对于提高模型的性能至关重要。

学会了如何使用sklearn库中的StandardScaler进行特征标准化，以及如何处理类别型数据。

通过在心脏病数据集上应用逻辑斯蒂回归，我了解了机器学习在医疗领域的应用，例如疾病预测、患者分类等。

通过这次学习和实践，我不仅掌握了逻辑斯蒂回归算法的理论知识和实践技能，而且提高了我的数据分析能力和编程能力。同时，这也激发了我对机器学习更深层次应用的兴趣，为未来的学习和研究奠定了坚实的基础。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/凡人多烦事01/article/detail/477393