太极图形学——高级数据结构——稠密

太极是一个面向数据的编程语言

在并行计算的框架下，在计算上花费的时间反而是少数，大量的时间都花在了数据获取（也就是访问内存）上面，这一点在之前的games103课程上也有简单的提及

cpu的计算能力非常强大，而gpu则不同，gpu的优势在于计算的同时进行，我们要提高gpu 的运算效率需要的是如何高效的访问内存

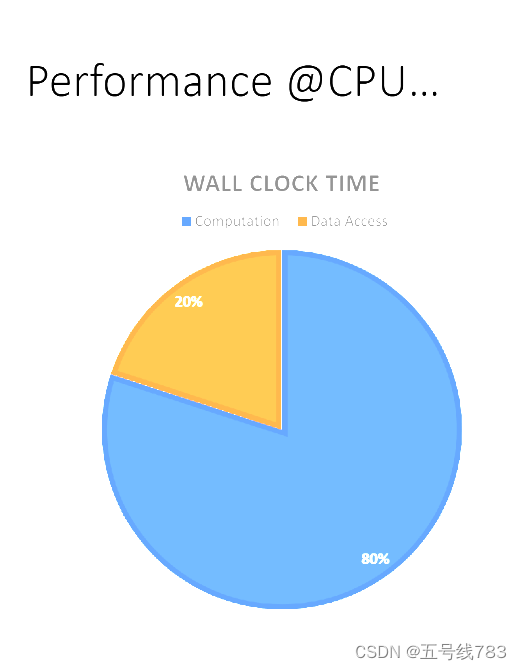
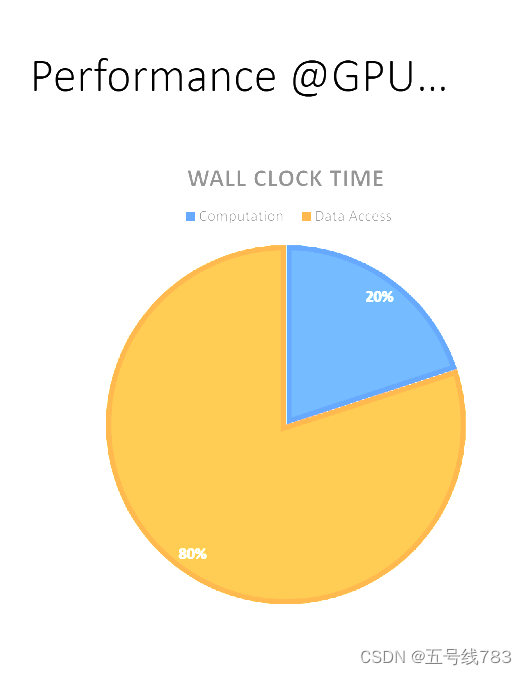
太极语言的快速性提现在两个方面，第一自然就是并行运算，第二则是数据获取的预缓存机制

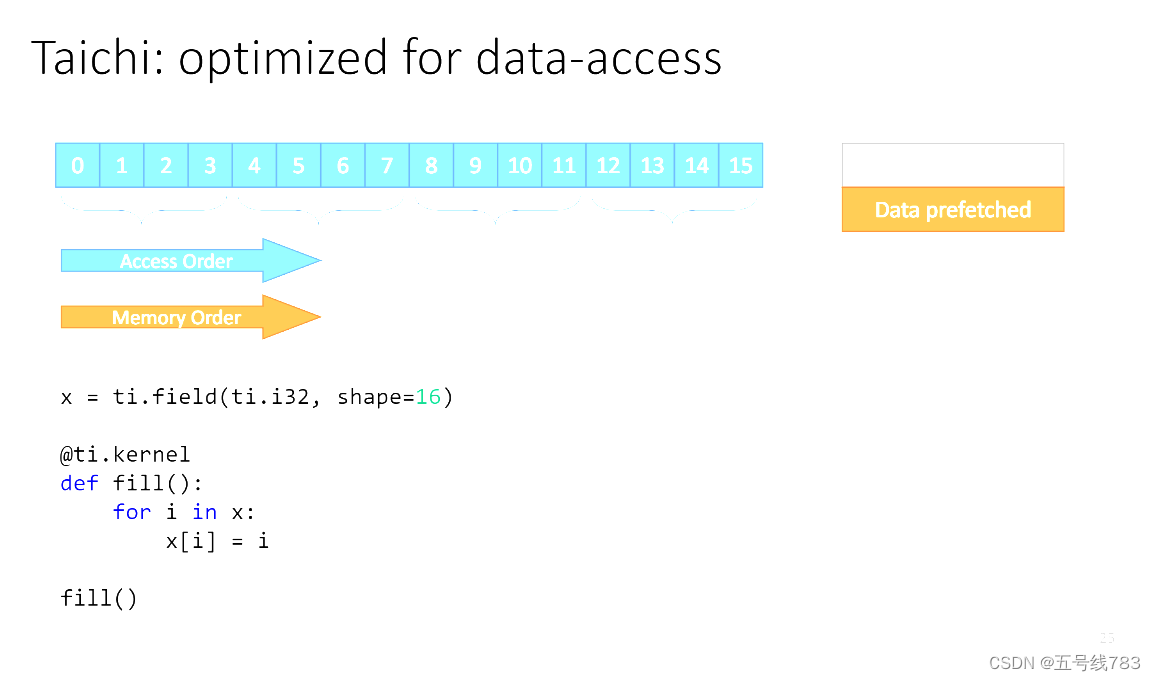
例如上面这个例子，首先定义了shape之后，在写入数据时并行处理，若是四线程的GPU处理，每一个单位填完第一个数字后（这个数字是从内存中取过来的），还会预缓存一段相邻的数字，这样填后面的数字是直接从缓存中直接取得，访问自然也就变快了

如果是多维数据呢？

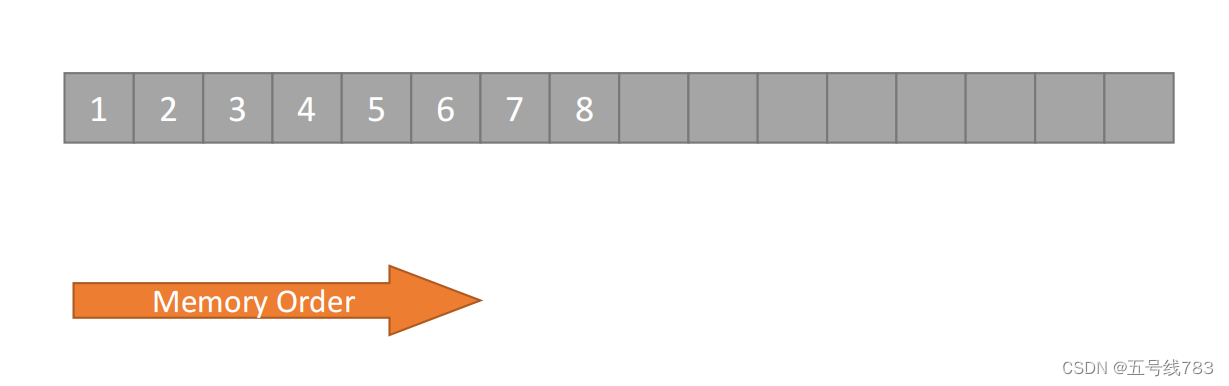
首先在内存中数据存储永远是一维的

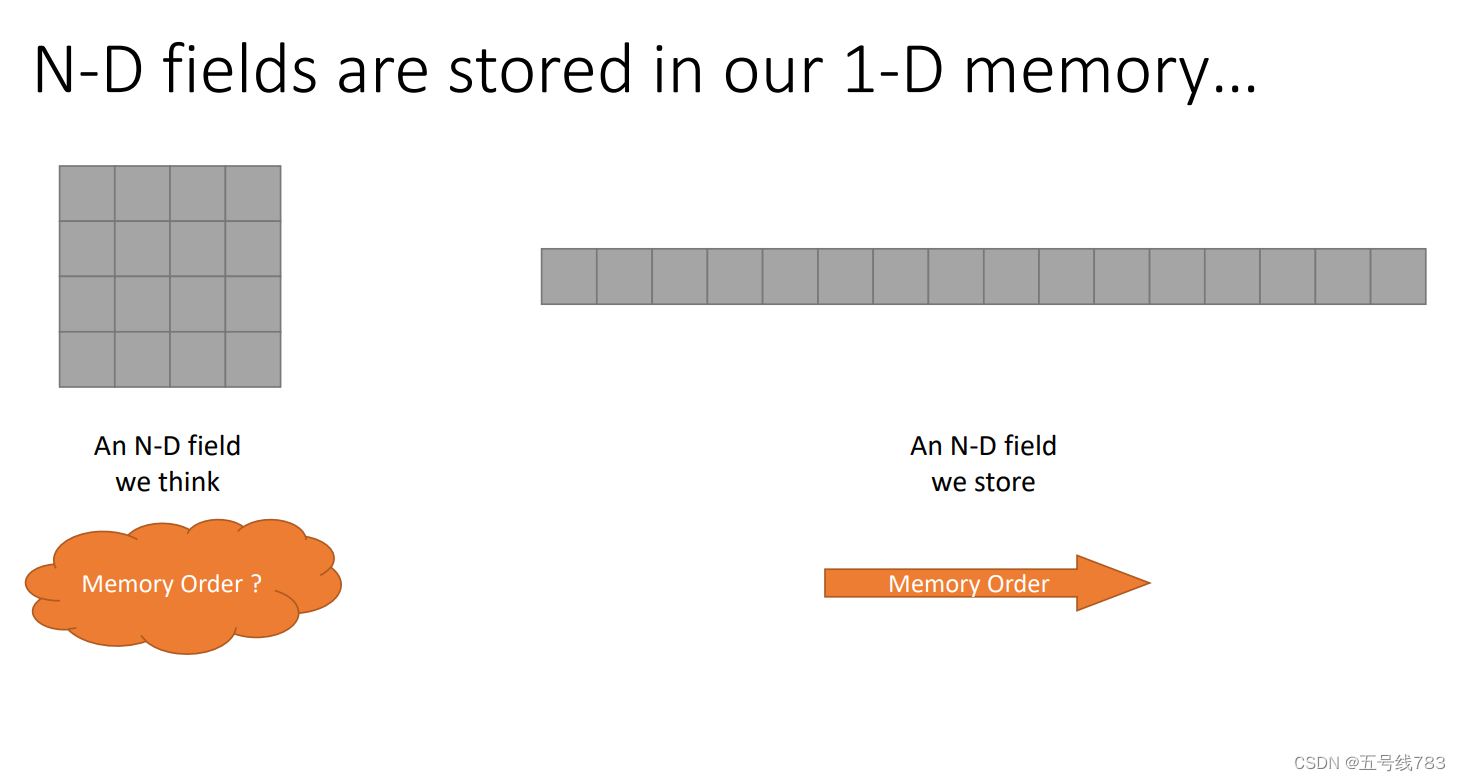
然而数据访问的模式确是不确定的

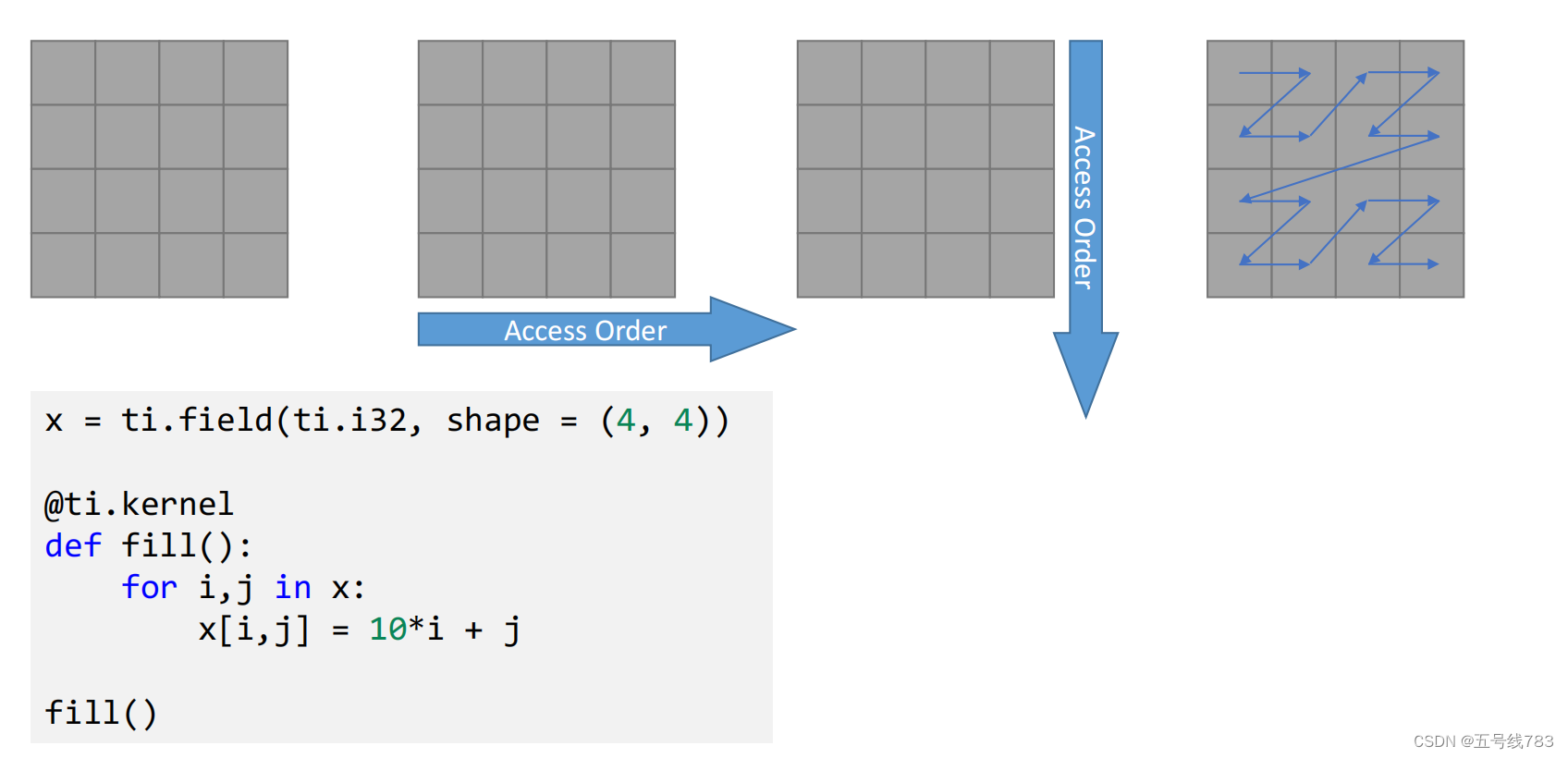
我们要将访问数据和内存数据联系起来，我们想要做的是数据访问友好化

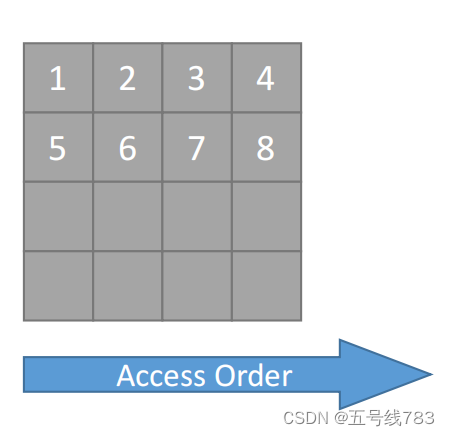
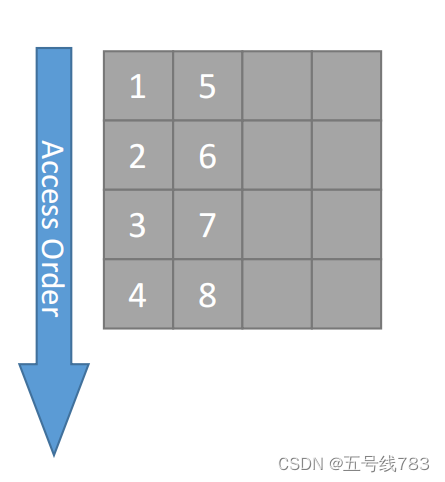
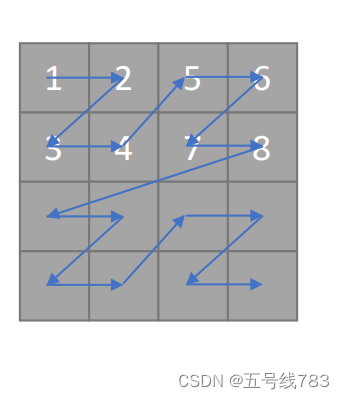
那么应该怎么存储数据呢，在C++中我们可以定义不同主序列的矩阵，如下所显示的逻辑，但这样做其实很不方便，需要人工记忆，很容易造成错误

那么在taichi的做法是这样的

x = ti.Vector.field(3,ti.f32,shape=16)#这是定义了一个场，这个场中是16个(1,3)的向量
 
#ti.root
x = ti.Vector.field(3,ti.f32) #先不给其shape
ti.root.dense(ti.i,16).place(x)#给x定义一个shape

 格式为这样

#转换例子
x = ti.field(ti.f32,shape=())
x = ti.field(ti.f32)
ti.root.place(x)
 
x = ti.field(ti.f32,shape=3)
x = ti.field(ti.f32)
ti.root.dense(ti.i,3).place(x)
 
x = ti.field(ti.f32,shape=(3,4))
x = ti.field(ti.f32)
ti.root.dense(ti.ij,(3,4)).place(x)
 
x = ti.Matrix.field(2,2,ti.f32,shape = 5)
x = ti.Matrix.field(2,2,ti.f32)
ti.root.dense(ti.i,5).place(x)

root出发，挂载的是dense，dense描述的形状，在dense后面挂着的就是那个没定义shape 的field

                          

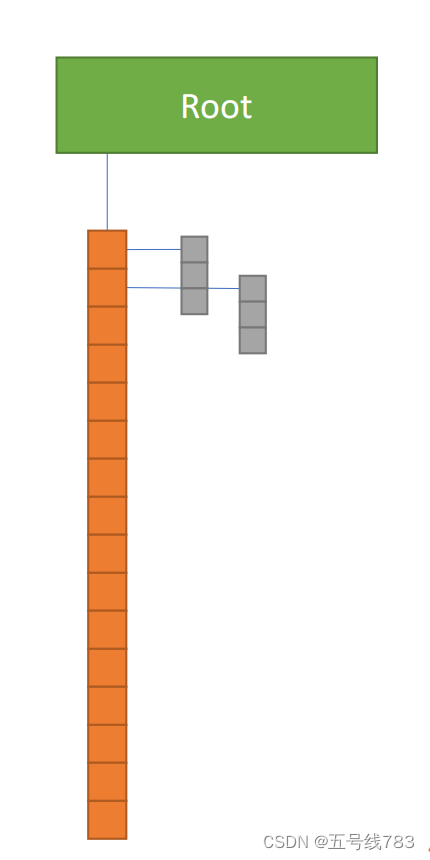
这样做的好处是可以更进一步的设计数据的结构

例如之前提出的那种矩阵形式的数据，就可以按下面的方式来存贮

这样我们就可以这样定义一个行主序列的field

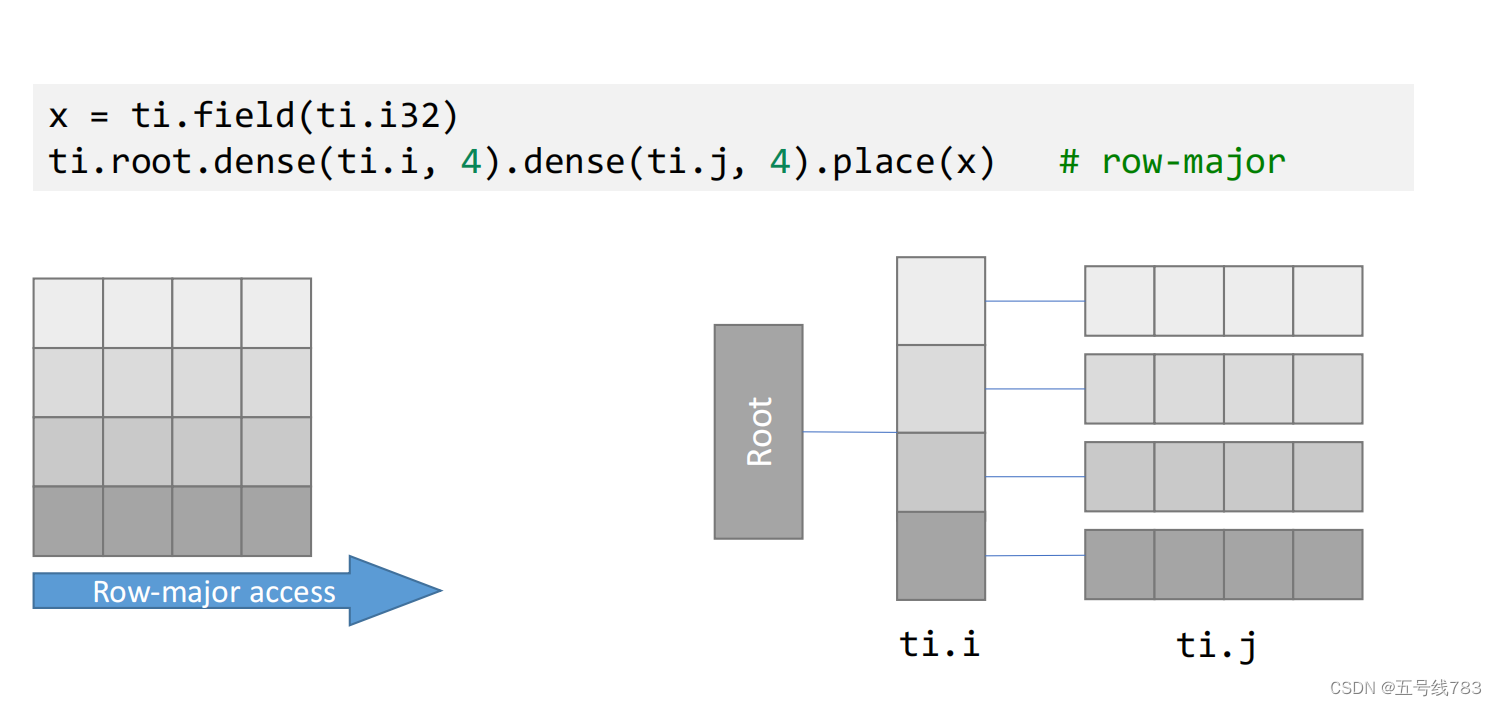
数据定义好之后，访问反而就很简单了，直接使用for语句就可以了

#以行为主序的field的定义
x = ti.field(ti.f32)
ti.root.dense(ti.i,4).dense(ti.j,4).place(x)
 
@ti.kernel
def fill():
    for i,j in x:
        x[i,j] = i*10+j

层级式的数据布局

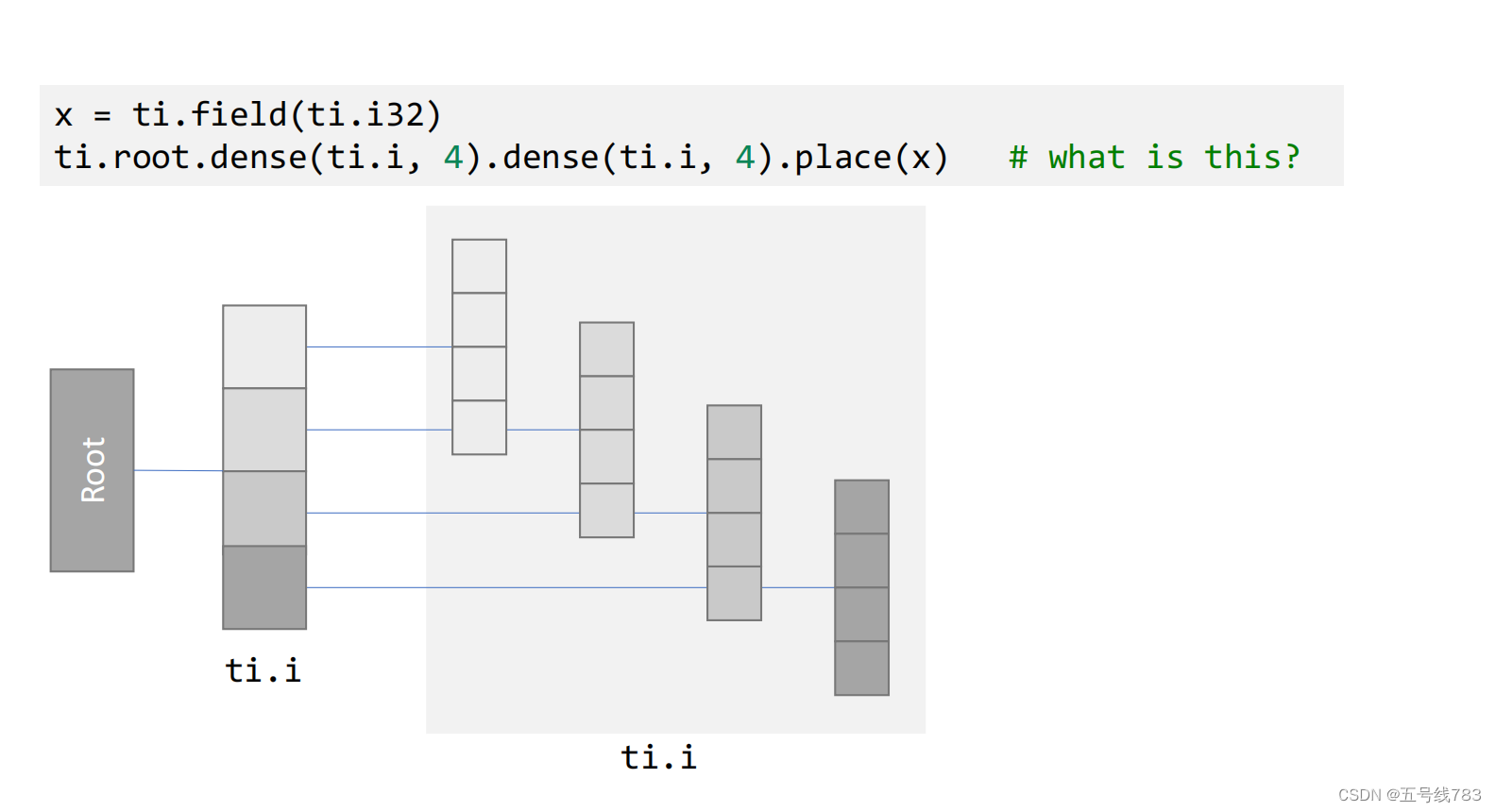
这主要使用在层级定义的方法，仍然可以用一维的方式去访问，但存储反而像是以二维的方式存储

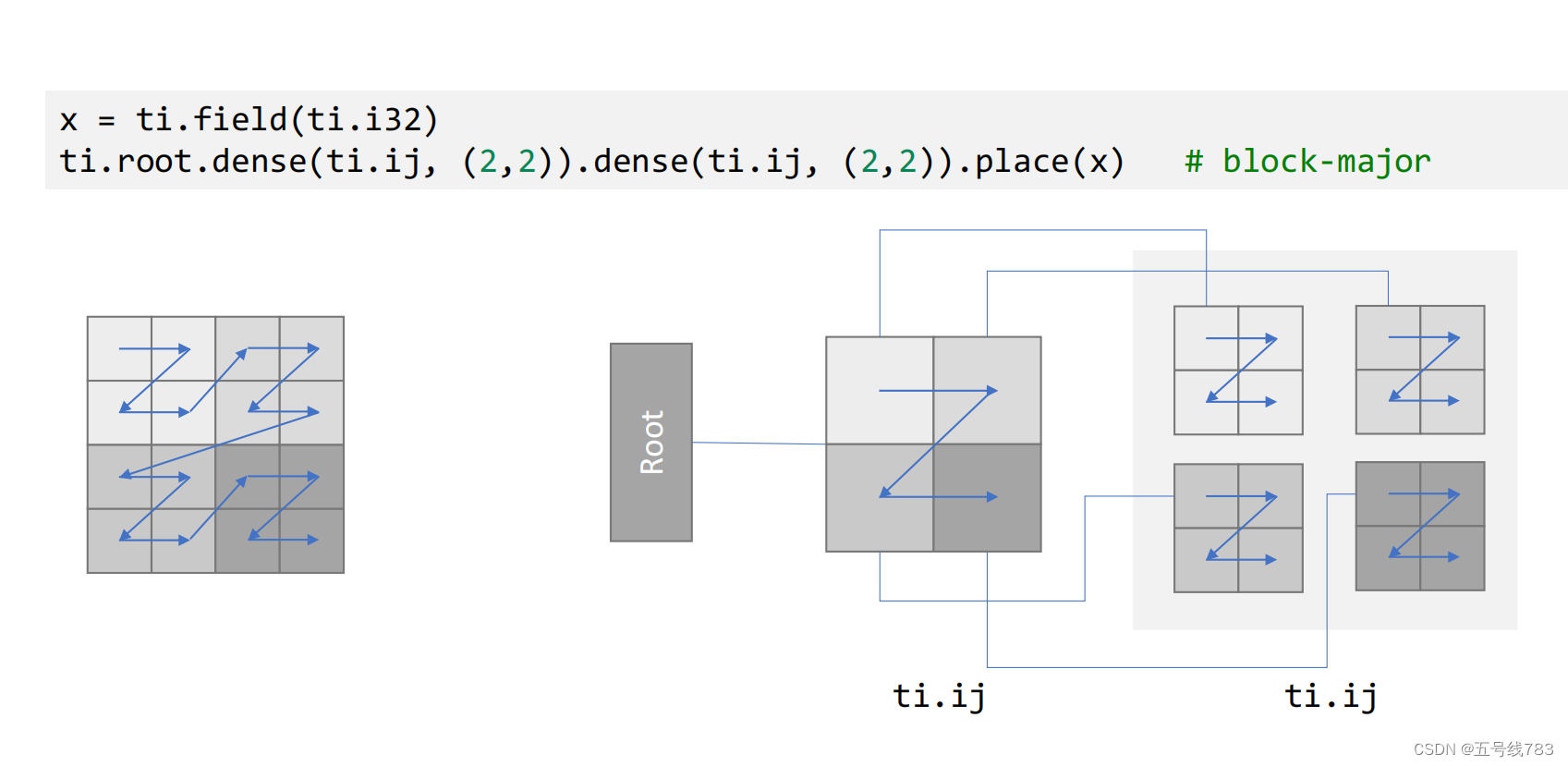
这个数据结构在插值等这种需要访问自己邻居的算法

soa存贮方式和aos存贮方式

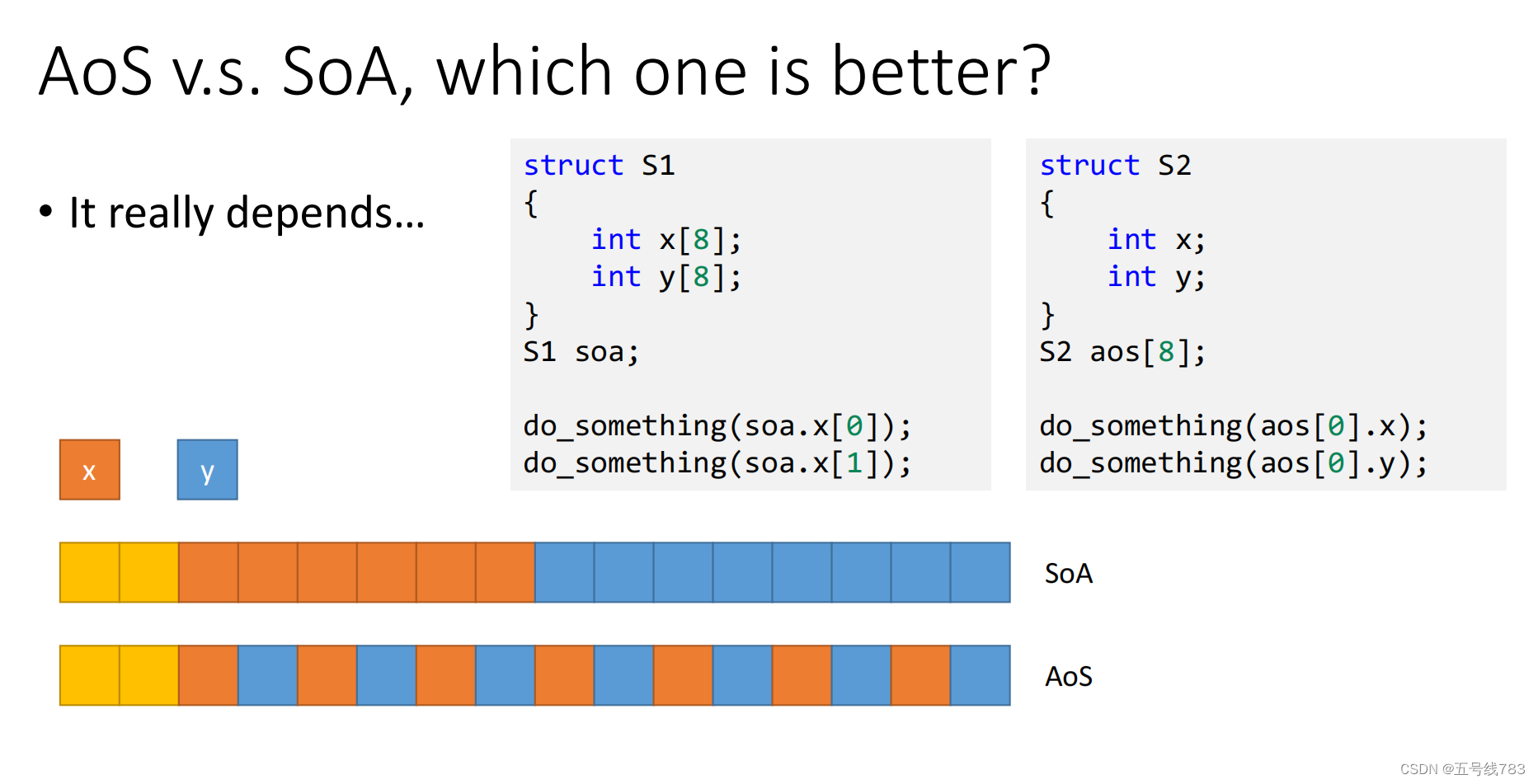
更改数据结构过后，后面的代码都不需要改

例如之间的数据