利用FFT分析比较卡尔曼滤波算法、低通滤波算法、滑动平均滤波的频谱_滑动平均为什么低通

1 卡尔曼滤波

详见博客 https://blog.csdn.net/moge19/article/details/81750731

2 低通滤波

2.1 算法推导

一阶RC滤波器的硬件电路如图：

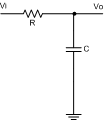
图中输入电压是Vi，电阻R，电容C，输出电压为Vo。

假设电路的输出阻抗很大（即不带任何负载），输入阻抗很小（理想情况）。可以得到以下公式：

$$V_o=\frac{1}{1+j\omega RC}{V}_i$$

电容的阻抗是$Z_C=\frac{1}{j\omega C}$。

而$\omega =2\pi f$

截止频率$f_{cut}=\frac{1}{2\pi RC}$，此频率下的信号，通过这个电路，输出电压和输入电压的关系式是$V_o=\frac{1}{1+j}{V}_i$

或者时域上的表达式：

$V_o=V_i-RC\frac{d{V}_o}{dt}$

上式离散后，可以得到：

$$V_o\left(k\right)=\frac{V_i\left(k\right)+\frac{RC}{T_s}{V}_o\left(k-1\right)}{1+\frac{RC}{T_s}}$$

2.2 算法实现

class RC_filter:
    def __init__(self,sampleFrq,CutFrq):
        self.sampleFrq = sampleFrq
        self.CutFrq = CutFrq
        self.adc_old=0
     
    def LowPassFilter_RC_1order(self,Vi):
        RC = 1.0/2.0/math.pi/self.CutFrq 
        Cof1 = 1/(1+RC * self.sampleFrq)
        Cof2 = RC* self.sampleFrq/(1+RC* self.sampleFrq)
        Vo = Cof1 * Vi + Cof2 * self.adc_old	 	
        self.adc_old = Vo
        return Vo  
1
2
3
4
5
6
7
8
9
10
11
12
13

3 滑动平均滤波

算法实现：

 noise_array =  np.random.normal(0, 400, noise_size)
    
    test_array_mean = [0]*32
    mean_array = []
    for i in range(noise_size):
        test_array_mean[i%32] = noise_array[i]
        mean_array.append(sum(test_array_mean)/32)
            
1
2
3
4
5
6
7
8

4 FFT转换比较

源数据频谱图：
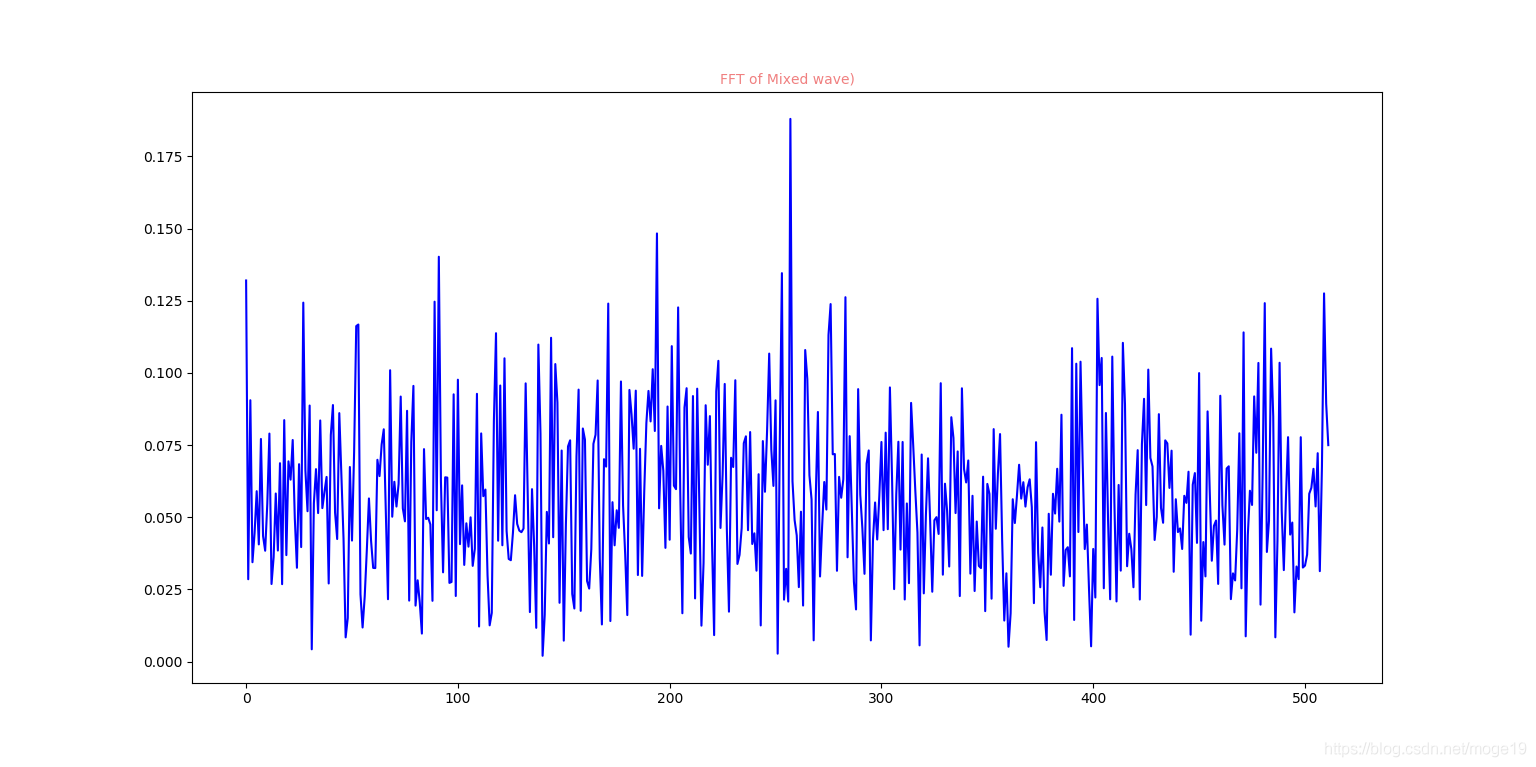卡尔曼滤波后的频谱
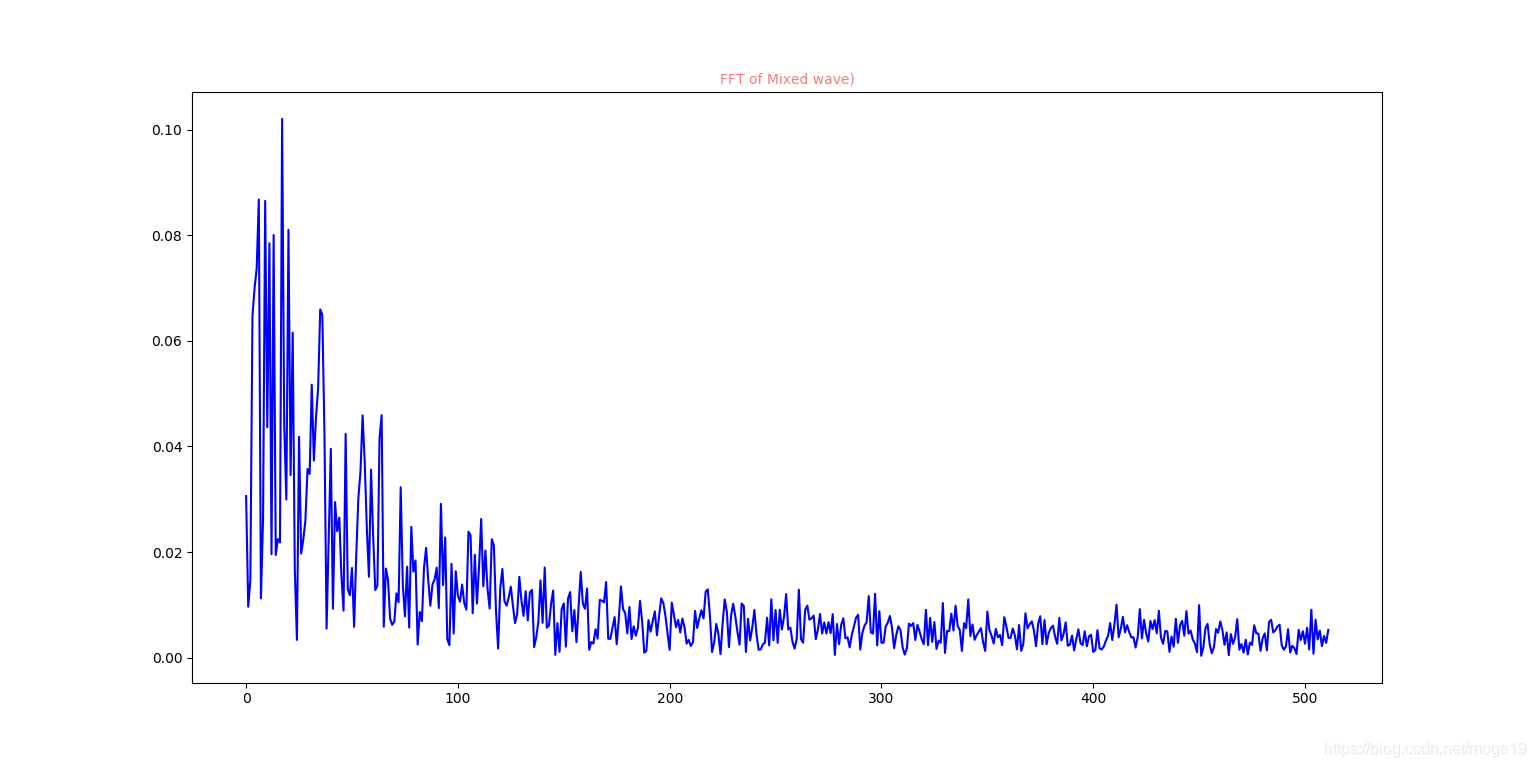RC滤波后的频谱
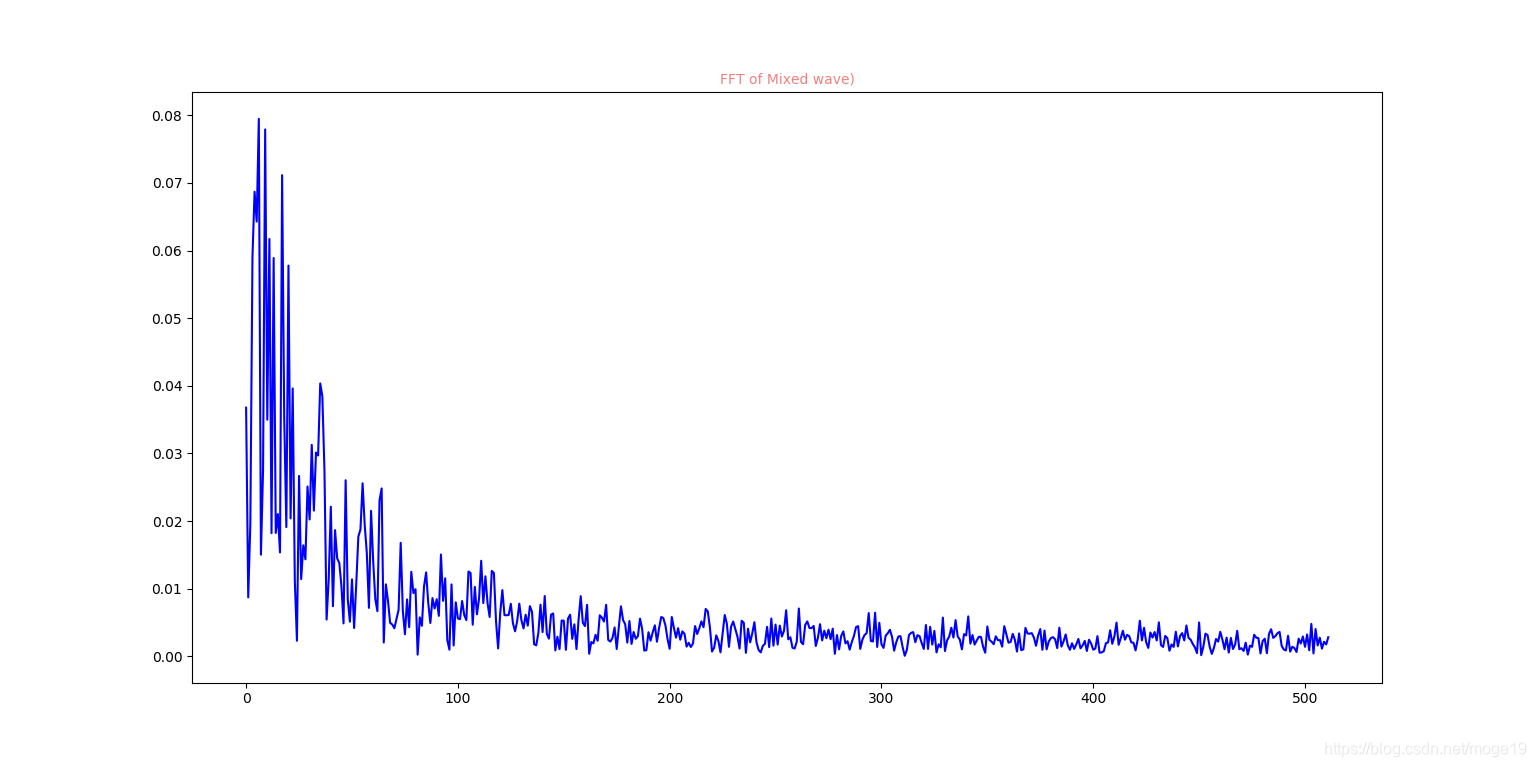从图中可以看出一阶的卡尔曼滤波与RC低通滤波的滤波效果一样
滑动平均滤波后的频谱图：
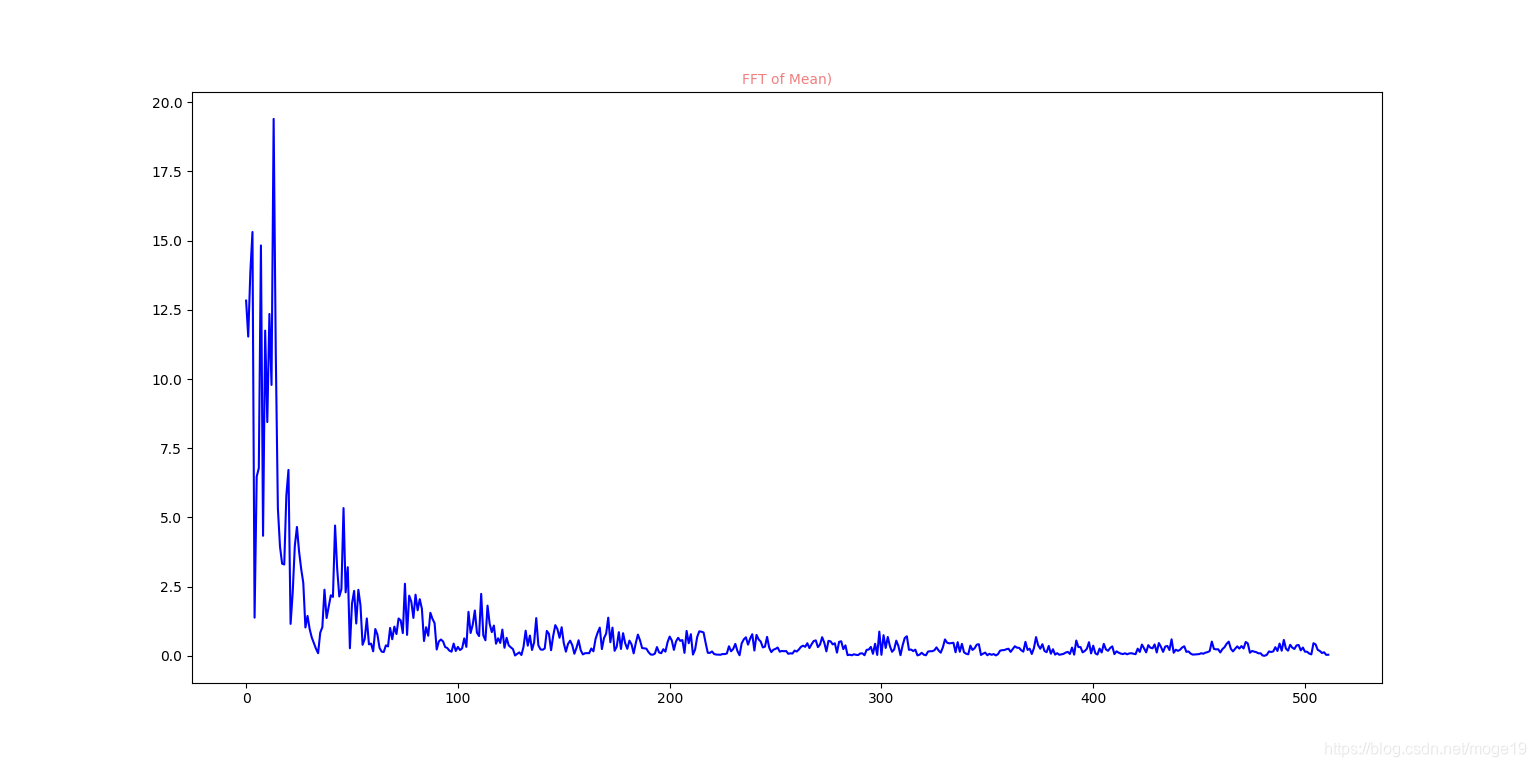从图中可以看出，滑动平均滤波，在低频段较之卡尔曼滤波和低通滤波，其频谱得到的幅值是其余二者的数十倍，这是由于求均值时，将部分噪声数据也计算到信号数据中导致的，因此可以看出，滑动平均滤波不能有效得将噪声数据滤掉，不过在工程因为计算简单，浮点运算少，甚至没有，所以得到广泛运用。

5 实现代码

# -*- coding: utf-8 -*-
"""
Created on Fri Feb 15 20:35:39 2019

@author: ASUS
"""

import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.fftpack import fft,ifft
class kalman_filter:
    def __init__(self,Q,R):
        self.Q = Q
        self.R = R
        
        self.P_k_k1 = 1
        self.Kg = 0
        self.P_k1_k1 = 1
        self.x_k_k1 = 0
        self.ADC_OLD_Value = 0
        self.Z_k = 0
        self.kalman_adc_old=0
        
    def kalman(self,ADC_Value):
       
        self.Z_k = ADC_Value
        
        #if (abs(self.kalman_adc_old-ADC_Value)>=60):
            #self.x_k1_k1= ADC_Value*0.382 + self.kalman_adc_old*0.618
        #else:
        self.x_k1_k1 = self.kalman_adc_old;
    
        self.x_k_k1 = self.x_k1_k1
        self.P_k_k1 = self.P_k1_k1 + self.Q
    
        self.Kg = self.P_k_k1/(self.P_k_k1 + self.R)
    
        kalman_adc = self.x_k_k1 + self.Kg * (self.Z_k - self.kalman_adc_old)
        self.P_k1_k1 = (1 - self.Kg)*self.P_k_k1
        self.P_k_k1 = self.P_k1_k1
    
        self.kalman_adc_old = kalman_adc
        
        return kalman_adc

class RC_filter:
    def __init__(self,sampleFrq,CutFrq):
        self.sampleFrq = sampleFrq
        self.CutFrq = CutFrq
        self.adc_old=0
       
        
    def LowPassFilter_RC_1order(self,Vi):
        RC = 1.0/2.0/math.pi/self.CutFrq 
        Cof1 = 1/(1+RC * self.sampleFrq)
        Cof2 = RC* self.sampleFrq/(1+RC* self.sampleFrq)
        Vo = Cof1 * Vi + Cof2 * self.adc_old	 	
        self.adc_old = Vo
        return Vo  

  
if __name__ == '__main__':
    noise_size = 1024
    noise_size_half = 512
    kalman_filter =  kalman_filter(0.01,0.5)
    RC_filter = RC_filter(400,5)
    noise_array =  np.random.normal(0, 2, noise_size)
    
        
    adc_value=[]
    
    for i in range(noise_size):
        adc_value.append(0)

    adc_value_noise = np.array(adc_value) + noise_array
    adc_filter_1=[]
    
    for i in range(noise_size):
        adc_filter_1.append(kalman_filter.kalman(adc_value_noise[i]))
    plt.plot(adc_value_noise,'r')
    plt.plot(adc_filter_1,'b')   

    #plt.plot(test_array)
    plt.show()
    adc_filter_2=[]
    plt.figure(1)
    for i in range(noise_size):
        adc_filter_2.append(RC_filter.LowPassFilter_RC_1order(adc_value_noise[i]))
    
    plt.plot(adc_value_noise,'r-')   
    plt.plot(adc_filter_2,'b')
    #plt.plot(test_array)
    plt.show()
    plt.figure(2)
    
  
    x = range(noise_size)
    y = noise_array
    #x=np.linspace(0,1,1400)      
    #设置需要采样的信号，频率分量有180，390和600
    #y=7*np.sin(2*np.pi*180*x) + 2.8*np.sin(2*np.pi*390*x)+5.1*np.sin(2*np.pi*600*x)
    
    yy=fft(x) #快速傅里叶变换 
    yreal = yy.real # 获取实数部分 
    yimag = yy.imag # 获取虚数部分 
    yf=abs(fft(y)) # 取绝对值 
    yf1=abs(fft(y))/len(x) #归一化处理 
    yf2 = yf1[range(int(len(x)/2))] #由于对称性，只取一半区间 
    xf = np.arange(len(y)) # 频率 
    xf1 = xf
    xf2 = xf[range(int(len(x)/2))] #取一半区间 
    """plt.subplot(221) 
    plt.plot(x[0:noise_size_half],y[0:noise_size_half]) 
    plt.title('Original wave') 
    plt.subplot(222) 
    plt.plot(xf,yf,'r')
    plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意这里的颜色可以查询颜色代码表 
              
    plt.subplot(223) 
    plt.plot(xf1,yf1,'g')
    plt.title('FFT of Mixed wave(normalization)',fontsize=9,color='r') """
    #plt.subplot(224) 
    plt.plot(xf2,yf2,'b') 
    plt.title('FFT of kalman_filter)',fontsize=10,color='#F08080') 
    plt.show()
    
    x = range(noise_size)
    y = adc_filter_2
    #x=np.linspace(0,1,1400)      
    #设置需要采样的信号，频率分量有180，390和600
    #y=7*np.sin(2*np.pi*180*x) + 2.8*np.sin(2*np.pi*390*x)+5.1*np.sin(2*np.pi*600*x)
    
    yy    = fft(x) #快速傅里叶变换 
    yreal = yy.real # 获取实数部分 
    yimag = yy.imag # 获取虚数部分 
    yf =abs(fft(y)) # 取绝对值 
    yf1=abs(fft(y))/len(x) #归一化处理 
    yf2= yf1[range(int(len(x)/2))] #由于对称性，只取一半区间 
    xf  = np.arange(len(y)) # 频率 
    xf1 = xf
    xf2 = xf[range(int(len(x)/2))] #取一半区间 
    """plt.subplot(221) 
    plt.plot(x[0:noise_size_half],y[0:noise_size_half]) 
    plt.title('Original wave') 
    plt.subplot(222) 
    plt.plot(xf,yf,'r')
    plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意这里的颜色可以查询颜色代码表 
              
    plt.subplot(223) 
    plt.plot(xf1,yf1,'g')
    plt.title('FFT of Mixed wave(normalization)',fontsize=9,color='r') """
    #plt.subplot(224) 
    plt.plot(xf2,yf2,'b') 
    plt.title('FFT of RC)',fontsize=10,color='#F08080') 
    plt.show()




1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160