热门标签
热门文章
- 1MySQL 5.7多源复制功能的应用_mysql 多源复制功能
- 2《农历算法》_农历程序算法
- 3Oracle 23ai——SQL*Plus新特性_oracle-free-23ai.service is not a native service
- 4代码助手Code Assistant,显示问题_oracle code asistant
- 5中台是不是要凉了_业务中台过时
- 6python——爬虫与脚本_python爬虫脚本
- 7带头结点的单链表实现快速、冒泡、直接插入/选择排序_插入hhh
- 8C C++最新手把手教你STM32入门教程(标准库)_stm32教程,2024年最新你还看不明白_stm32 c++
- 9建议收藏!小米java社招面试_小米java外包面试题,面试加分项目能加多少分啊_小米java面试题
- 10Windows10 安装python3.64 cuda9.0 cudnn 完整版(大马哈鱼)_python的cudu安装
当前位置: article > 正文
【贪吃蛇问题】_可能有不少的同学玩过“贪吃蛇“的游戏,游戏中蛇头带动整个蛇的移动,蛇身将沿蛇头
作者:喵喵爱编程 | 2024-08-19 08:40:11
赞
踩
可能有不少的同学玩过“贪吃蛇“的游戏,游戏中蛇头带动整个蛇的移动,蛇身将沿蛇头
问题:
可能有不少的同学玩过“贪吃蛇“的游戏,游戏中蛇头带动整个蛇的移动,蛇
身将沿蛇头移动过的位置进行移动。如果将整条蛇分成若干个方格,则可以表示为
S1,S2,S3,…,SL,其中 S1 为蛇头,SL 为蛇尾,中间则是蛇头到蛇尾之间的部分。蛇在某
个区域内移动时,如果蛇头所在位置的上下左右四个方向没有其它的物体,则蛇头 S1 可以
朝其中任何一个方格移动,蛇身则填补前面移动后的区域,也就是 S2 移动到 S1 所在区域,
S3 移动到 S2 所在区域……,依次类推,如下图所示。
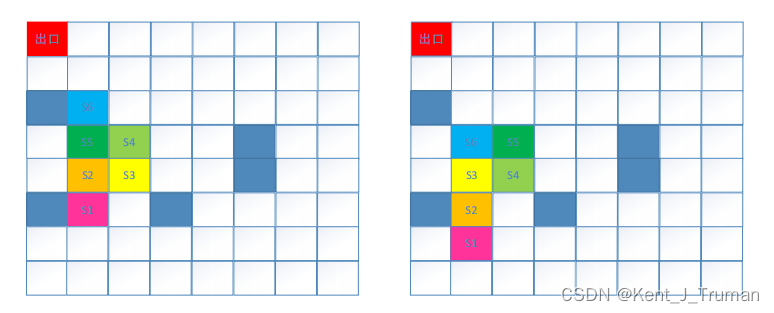
备注:左图为蛇移动前的情况。右图为蛇向下移动一个方格后的情况。蓝色填充的方格
表示有障碍物。
请判断蛇是否可以从它当前所在的位置移动到出口所在的位置,如果能,则给出最少需
要移动的步数。如果不能,则输出“Impossible”。
输入要求:
输入的第 1 行包含三个整数 n, m(l<=n, m<=20) 和 L (2<=L<=8),分别表示蛇所在区域的大小(行,列方格数)以及蛇的长度。其后的 L 行用于表示从蛇头到蛇尾依次占用的
方格的行列值。紧接着的 1 行包含一个整数 K,表示该区域内障碍物占用的方格数。之后的
K 行,每行包含两个整数,分别表示障碍物所占用的方格的行列值。出口所在的位置为(1,
1),且出口处没有障碍物。
输出要求:
输出 1 行,如果蛇能够到达出口,则输出蛇从当前位置移动到出口位置最少需要移动的
方格数量,否则输出“Impossible”。
样例输入:
8 8 6
6 2
5 2
5 3
4 3
4 2
3 2
5
3 1
6 1
4 6
5 6
6 4
样例输出:
12
思路:
代码(6.7更新,把sign去掉了):
- #include<bits/stdc++.h>
- using namespace std;
- #define exit_x 1
- #define exit_y 1
-
- int n, m, l, k;
- int dx[] = {-1, 0, 0, 1};
- int dy[] = {0, -1, 1, 0};
- int best = INT_MAX;
-
- int solve(int **blocks, int h, int t, int *snake_x, int *snake_y, int total)
- {
- int result = INT_MAX;
-
- if(total >= best) return total;
-
- int head_x = snake_x[h], head_y = snake_y[h];
-
- if(head_x == exit_x && head_y == exit_y)
- {
- best = total;
- return total;
- }
-
- for(int i = 0; i < 4; i++)
- {
- int new_x = head_x + dx[i];
- int new_y = head_y + dy[i];
-
- if(new_x < 1 || new_x > n || new_y < 1 || new_y > m) continue;
- if(blocks[new_x][new_y]) continue;
-
- bool hurt = false;
- for(int j = 0; j < l; j++)
- {
- if(snake_x[j] == new_x && snake_y[j] == new_y) hurt = true;
- }
- if(hurt) continue;
-
- int tempx = snake_x[(h-1+l)%l], tempy = snake_y[(h-1+l)%l];
-
- snake_x[(h-1+l)%l] = new_x;
- snake_y[(h-1+l)%l] = new_y;
-
- int this_time = solve(blocks, (h-1+l)%l, (t-1+l)%l, snake_x, snake_y, total+1);
- if(this_time < result) result = this_time;
-
- snake_x[(h-1+l)%l] = tempx;
- snake_y[(h-1+l)%l] = tempy;
-
-
- }
-
- return result;
- }
- void Delete(int **blocks, int *snake_x, int *snake_y)
- {
- for(int i = 1; i <= n; i++)
- {
- delete [] blocks[i];
- }
-
- delete [] snake_x;
- delete [] snake_y;
- }
- int main()
- {
-
- cin >> n >> m >> l;
- int **blocks = new int*[n+1];
- for(int i = 1; i <= n; i++)
- {
- blocks[i] = new int[m+1]();
- }
-
- int *snake_x = new int[l+1]();
- int *snake_y = new int[l+1]();
- for(int i = 0; i < l; i++)
- {
- cin >> snake_x[i] >> snake_y[i];
- }
-
- cin >> k;
- for(int i = 1; i <= k; i++)
- {
- int x, y;
- cin >> x >> y;
- blocks[x][y] = 1;
- }
-
- int steps = solve(blocks, 0, l-1, snake_x, snake_y, 0);
-
- if(steps == INT_MAX) cout << "Impossible" << endl;
- else cout << steps << endl;
-
- Delete(blocks, snake_x, snake_y);
- return 0;
- }

本文内容由网友自发贡献,转载请注明出处:https://www.wpsshop.cn/w/喵喵爱编程/article/detail/1001549
推荐阅读
相关标签


