排序进阶----快速排序

        当我们写了插入和希尔排序后，我们就应该搞更难的了吧。大家看名字就知道我们这篇博客的内容了吧。而且从名字上来看。快速排序就很快吧。那么为什么这个排序怎么能叫快速排序啊。我们希尔排序不是很快嘛。那么我们的快速排序肯定是有特殊之处嘞。不然这就太自负了。而且对于快速排序是用上了我们以前学的知识，二叉树。那我们为什么这么说嘞。我们下面就来讲讲嘛。

快速排序的思路

       其实对于看快速排序来说，我们理解的话还算是比较简单的。为什么这么说了，因为大家都已经大概了解了二叉数的用法了吧。我们这个快速排序设置一个值，但是这个值就是数组里面的，然后以他为主来左右行走。就是数组的头和尾，然后向中间寻找遇见比他大或者比他小的数，然后就进行交换，直到他们相遇。他们如果相遇了，那么可以表明的一件事就是他们相遇的地点一定会比我们设定的值大或者小。那么之所以会这样子呢，我们后面在实现的时候再谈论。所以总之上面我们说的就是把这个数组从左右两边开始移动后边的如果比我们设定值小，就先暂时停留，然后左边向中间移动，如果遇见比我们设定的值大的话就暂时停留，然后他们两个交换。接着继续往前走，如果他们两个相遇了的话，我们也能确定他们相遇的值是否比设定的值大或者小。后当他们相遇了之后，这就能用上我们二叉树的内容了。然后我们分左边和右边递归来实现这个。

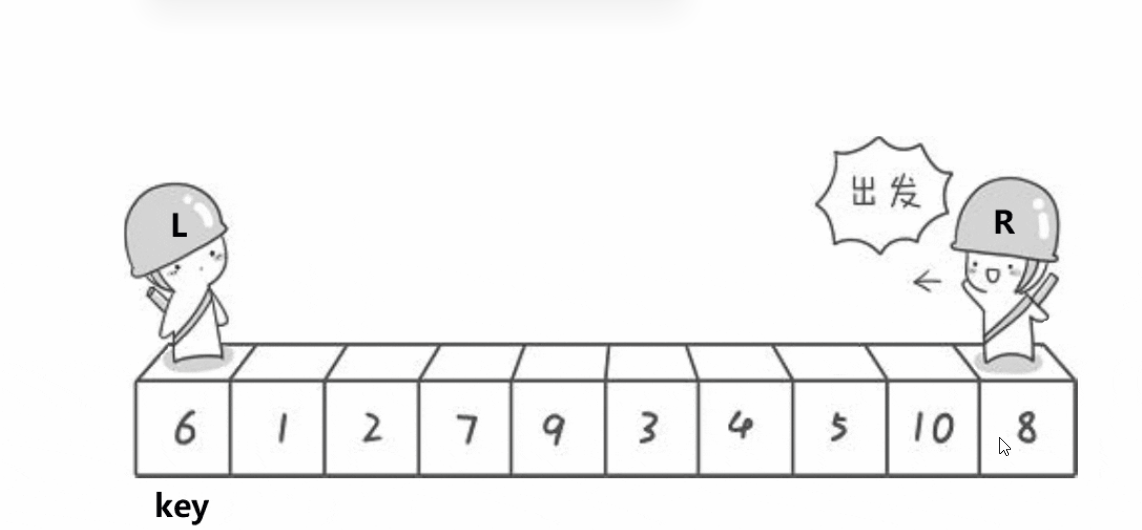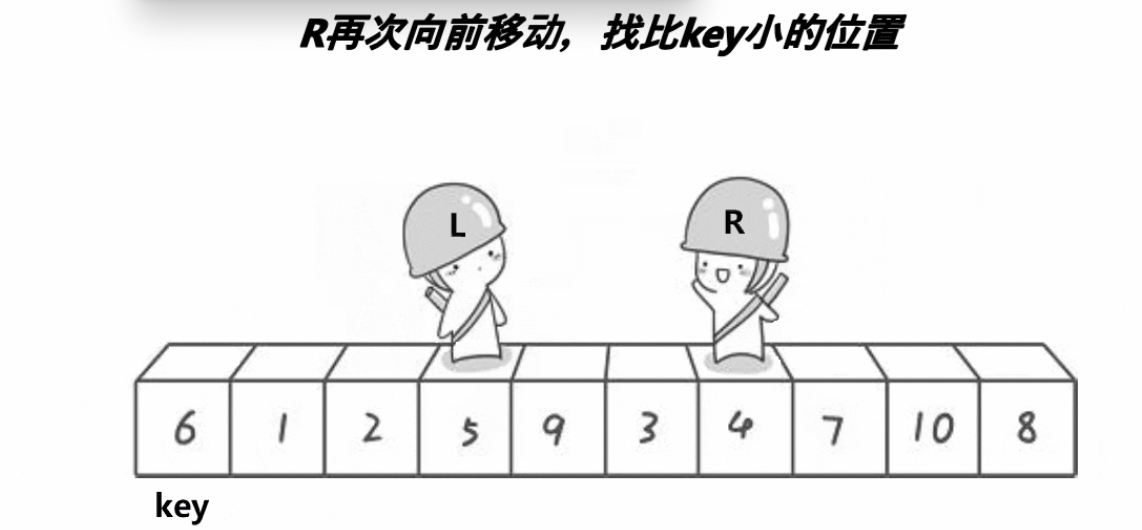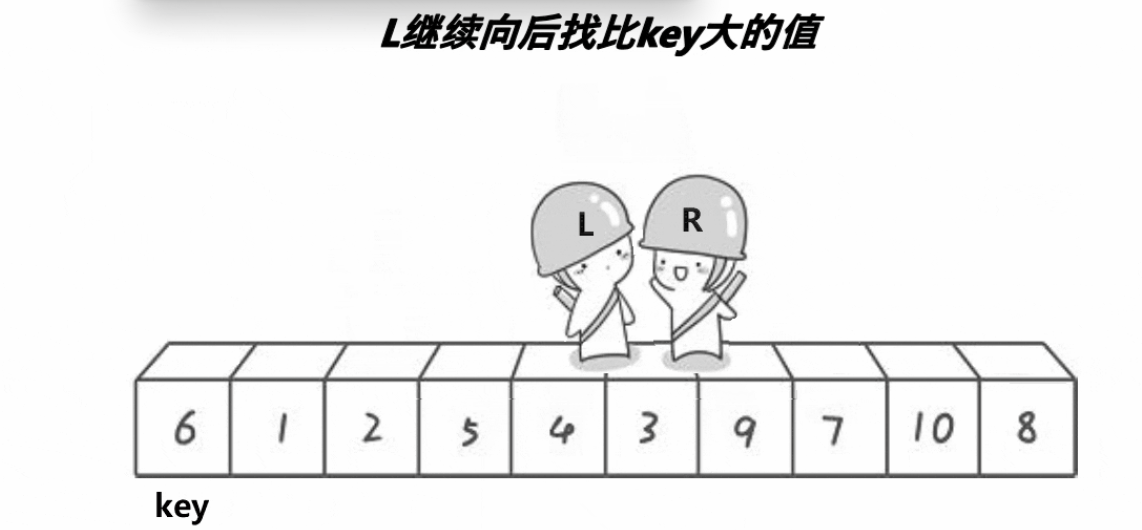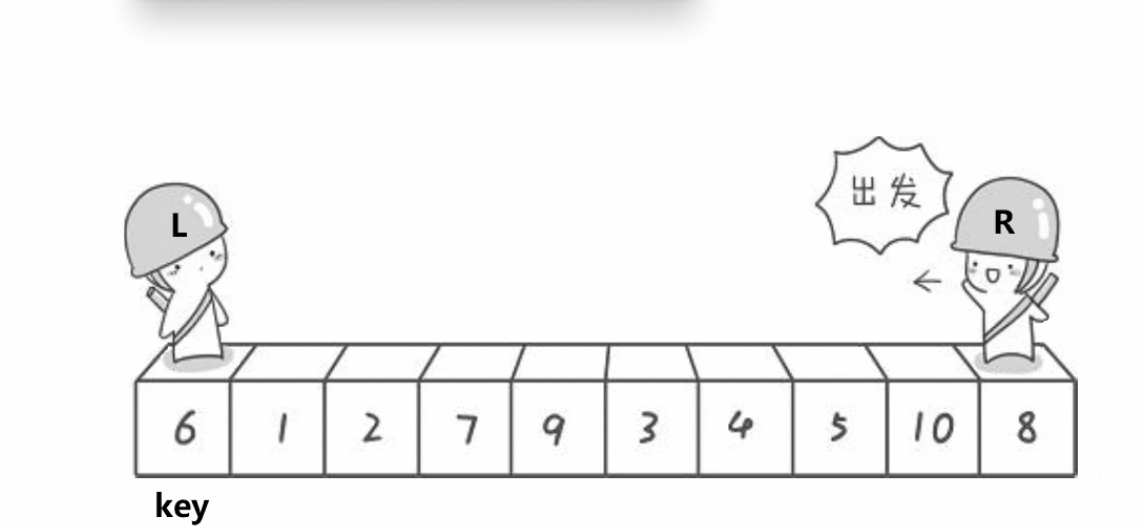
快速排序的实现 

       当然实现快速排序的话，我们也还是像以前一样。先来写一个单趟。然后再实现整整体的过程。那么我们上面也说过了，需要先设定一个基准值。那我就先普遍设为头节点。当我们设置头节点后，我们还要向左右移动。那么我们这个还要再设置两个。那我当我们设置完这些之后，我们就可以开始向中间移动了。但是移动我们也有一个先后吧，到底是左先动还是右先动？如果我们以右先动的话，那么就是先找比我们设定值小的值就停下来然后就是左边移动。那么就会遇见比设定值小的值停下来。当达到这个目标之后我们就进行交换。知道他们两个相遇之后就结束。然后与这个值与我们的设定值进行交换。大家可能会想你怎么知道他们相遇的值会我设定的值小？这个大家需要先想一下。我们是让右边先走的。如果他们相遇，那肯定是右边走到了比他小的子才会停下来。然后左边才走。那么这是不是就确定了他们相遇的值比设定的值小。那么我们已经退出循环了，所以我们需要在手动的调整一下。这样，我们这单趟就结束了。

void xixi(int* a, int zuo, int you)
{
	//key确定基准值
	int key = zuo;
	int left = zuo;
	int right = you;
	while (left < right)
	{
		//right先行动，找到比key小的值
		while (left < right && a[right] >= a[key])
		{
			right--;
		}
		//left行动，找到比key大的值
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		//到达指定位置，进行交换
		swap(&a[left], &a[right]);
	}
	//走完上面的步骤后，两个下标会相聚在一个位置
	//然后对这两个位置的值进行交换
	swap(&a[right], &a[key]);
}

        上面就是快速排序的单趟排序了，看起来是不是还是比较简单啊。就是比较确定下标然后交换数组的值。那么我们刚开始说过 快速排序是会用到二叉树的内容。我们既然单趟了那么下一趟怎么走呢？我不知道日常树就是递归值不一样而已。那么我们只需要将传进去的递归值改变从他们两个相遇的地方划分成为两部分，然后分为左部分和右部分。然后再分别理赔，周而复始，这样就排序好了。大家想想是不是这样的？所以在单趟排序的时候，我们还有一个事情需要处理一下，就是将key的值改变我们在最后的交换把key的改变写上，然后递归实现。

void QuickSort(int* a, int begin, int end)
{
	//结束条件
	if (begin >= end)
	{
		return;
	}
	//一趟的实现
	int left = begin;
	int right = end;
	int keyi = left;
	while (left < right)
	{
		//右边开始行动   一定要加上等于，因为快速排序找的是一定比它小的值
		while (left < right && a[keyi] <= a[right])
		{
			right--;
		}
		//左边开始行动
		while (left < right &&   a[left] <= a[keyi])
		{
			left++;
		}
		swap(&a[left], &a[right]);
 
	}
	swap(&(a[keyi]), &(a[right]));
	keyi = right;
	//[begin,keyi-1] keyi [keyi+1,end]
	QuickSort(a, begin, keyi - 1);//递归传递值
	QuickSort(a, keyi + 1, end);
}

         上面就是快速排序的基本方法了。当然都说只是基本方法了，那么他肯定还可以再进行优化。那他有哪些地方可以优化呢？我们接下来就来讲讲这些。

快速排序的优化 

1：      首先我们对于快速排序的优化就是我们最重要的key的值。我们快速排序，为什么key的值就始终是头节点了，我们不能换一个更加好一点儿的吗？所以我们的快速优化的第一个就是更改key的值。那么我们需要递归很多事，所以key的值需要更换很多次。那么我们就要写一个子函数来专门确定key的值。但是如何确定啊？这里就要用前辈的思想了。叫做三数取中。我们传递数组，和开头和结尾，然后我们计算开头和结尾中间的值比较，我们取中间的值，这样我们的快速排序就更加快速了。实现很简单：

//三数取中
int GetMid(int *a, int begin, int end)
{
	int mid = (begin + end) / 2;//平均的下标值
	if (a[begin] > a[end])//假设头大于尾的话
	{
		if (a[end] > a[mid])//尾大于平均那么尾就是中间的
			return end;
		else if (a[mid] > a[begin])//如过平均大于头的话头是中间值
			return begin;
		else//就只剩平均值了
			return mid;
	}
	else//(a[begin] < a[end])假设头大小于尾的话
	{
		if (a[end] < a[mid])//平均大于尾。则为是中间
			return end;
		else if (a[begin] < a[mid])//平均大于头的话，平均就是中间
			return mid;
		else//就只剩头了
			return begin;
	}
}

2:          另外一个优化方法就简单粗暴了许多了。因为我们都说快速排序嘛，要比我们前面学了几个排序都要好一些，而且我们也知道我们前面写的几个排序中插入排序对。小数组计算更快。我们就判断如果数组大于十的话，我们就快拍，如果小于十的话，我们就用插入排序。这就是大的用大的方法，小的用小的方法，这样我们是不是要方便许多？ 但是我们要注意1.插入排序之后两个参数，一个是数据集合的起点地址，第二个是数据量。2.使用插入排序时，我们要传入待排序数据集合的其实地址，即a+begin，如果传入的是a，那排序的永远都是数组a的前n个区间。3.插入排序传入的是数据个数，所以我们要将end-begin加上1之后才传入。快速排序中end、begin都是闭区间(即数组下标)。如果大家对于插入排序还是不了解的话，可以看一下我上一篇博客。

void QuickSort_Pointer(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//数据区间大与10，进行快速排序
	if (end - begin > 10)
	{
		int prev = begin;
		int cur = begin + 1;
		int keyi = begin;
		//三数取中后对keyi位置的值进行交换
		int mid = GetMid(a, begin, end);
		swap(&a[mid], &a[keyi]);
		while (cur <= end)
		{
			if (a[cur] < a[keyi] && ((++prev) != cur))
			{
				swap(&a[cur], &a[prev]);
			}
			cur++;
		}
		swap(&a[prev], &a[keyi]);
		keyi = prev;
		//开始进行递归
		QuickSort_Pointer(a, begin, keyi - 1);
		QuickSort_Pointer(a, keyi + 1, end);
	}
	else
	{
		//左闭右闭
		InsertSort(a, end - begin + 1);
		InsertSort(a + begin, end - begin + 1);
	}
 
}

总结

      那么说明的就是我们快速拍摄的大概所有内容了。当然还有一种优化其实也是可以的，叫做挖坑法。这个如果大家感兴趣的话可以自己去了解一下。当然我的内容是不是很完全的。所以大家可以在评论区里面也说一下，自己感兴趣的话，我下一篇博客会补充的。