Python多元线性回归_简单的多元线性回归数据集

Python多元线性回归

1.首先导入需要的模块

import pandas
from sklearn.model_selection import train_test_split #交叉验证 训练和测试集合的分割
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
1
2
3
4
5

2.数据集使用的是Advertising.csv；总共两百条数据，记录的是广告投入与销售之间的关系。之间关系如下
Sales = TVx1+Radiox2+Newspaper*x3+b；

3.读取数据

# 读取csv数据
data = pandas.read_csv("csv//Advertising.csv");

1
2
3

4.构建X和Y特征向量

# 构建X和Y   scikit-learn要求X是一个特征矩阵，y是一个NumPy向量。pandas构建在NumPy之上。
# 因此，X可以是pandas的DataFrame，y可以是pandas的Series，scikit-learn可以理解这种结构
X = data[['TV','Radio','Newspaper']];  #返回 dataframe
print(type(X),"  ",X.shape);   # 返回X类型  X的维度
Y = data['Sales']; #返回Series类型  及list
print(type(Y),"   ",Y.shape);  # 返回X类型  X的维度
1
2
3
4
5
6

输出

5.拆分训练集和测试集

#  训练集测试集拆开 百分之75用于训练 百分之25用于测试
# random_state 在需要设置random_state的地方给其赋一个值，当多次运行此段代码能够得到完全一样的结果，别人运行此代码也可以复现你的过程。若不设置此参数则会随机选择一个种子，执行结果也会因此而不同了。虽然可以对random_state进行调参，但是调参后在训练集上表现好的模型未必在陌生训练集上表现好，所以一般会随便选取一个random_state的值作为参数。
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,random_state=1);
print(X_train.shape,"  ",X_test.shape,"  ",Y_train.shape,"  ",Y_test.shape);
1
2
3
4

输出

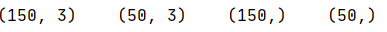
6.线性回归

# sklearn线性回归
lrg = LinearRegression();
model = lrg.fit(X_train,Y_train);  #训练
print(model);
print(lrg.intercept_);  #输出截距
coef = zip(['TV','Radio','Newspaper'],lrg.coef_) #特征和系数对应  打包对应为元组
for T in coef :
    print(T); #输出系数
1
2
3
4
5
6
7
8

输出

7.预测

#预测
y_pred = lrg.predict(X_test);
print(y_pred);  #输出测试值
1
2
3

输出

8.#评价测度

#评价测度  对于分类问题，评价测度是准确率，但其不适用于回归问题，因此使用针对连续数值的评价测度（evaluation metrics）。
# 这里介绍3种常用的针对线性回归的评价测度。·
# 平均绝对误差（Mean Absolute Error，MAE）；
# ·均方误差（Mean Squared Error，MSE）；
# ·均方根误差（Root Mean Squared Error，RMSE）。这里使用RMES进行评价测度。
print("预测");
print(type(y_pred),type(Y_test));
print(len(y_pred),len(Y_test));  #  len() 方法返回对象（字符、列表、元组等）长度或项目个数。

sum_mean = 0;
for i in range(len(y_pred)):   #for循环
    sum_mean+=(y_pred[i]-Y_test.values[i])**2;
sum_erro = np.sqrt(sum_mean/len(y_pred));  # sqrt()根号  均方根误差
print("均方根误差",sum_erro);
1
2
3
4
5
6
7
8
9
10
11
12
13
14

输出

9.绘制ROC曲线

plt.figure();
plt.plot(range(len(y_pred)),y_pred,'b',label="predict");   #x: x轴上的数值 y: y轴上的数值 ls：折线图的线条风格 lw：折线图的线条宽度 label：标记图内容的标签文本
plt.plot(range(len(Y_test)),Y_test,'r',label="test");
plt.xlabel("the number of sales");
plt.ylabel("value of sales");
plt.legend();  # 用于显示plot函数里面 label标签
plt.show();
1
2
3
4
5
6
7

输出