- 1海量数据处理---分而治之_如何使用分治算法处理海量数据
- 2Qt Creator 添加自定义新建文件/项目模板向导_修改qt源码自定义添加项目模板
- 32020年大数据营销案例_大数据营销案例分析_2020年利用大数据预测的案例
- 4Java使用GSON对JSON进行解析——IDEA引入jar包方式_gson jar
- 5创建ArrayList的几种方式_arraylist创建
- 6在Linux离线安装SQL,在Linux上离线安装SQL Server 2017
- 7js实现公告栏文字从右向左匀速循环滚动,且公告内容可以随时增减
- 8详解基于Android的Appium+Python自动化脚本编写_安卓自动化脚本开发
- 9曼昆 宏观经济学 笔记 10.21备份_zy=f(zk,zl)
- 10机器学习入门--LSTM原理与实践_sklearn lstm
Mamba论文_mamba ssm s6 选择性扫描
赞
踩
题目
Mamba: Linear-Time Sequence Modeling with Selective State Spaces
Mamba:具有选择性状态空间的线性时间序列建模
作者简介
Albert Gu
Tri Dao

状态空间模型SSM
详细网站
https://blog.csdn.net/weixin_39699362/article/details/136295477
定义
结构状态空间模型(Structural State Space Model, SSM)是一种用于描述和分析时间序列数据的数学模型。它通过显式地表示时间序列数据的潜在结构(即状态)以及这些状态随时间的演变方式,来捕捉数据的动态特性和复杂的依赖关系。
1. 基本概念
- 状态变量(State Variables): 这些是隐藏的(不可观测的)变量,代表系统的潜在状态。它们随时间变化,反映了系统内部的动态特性。
- 观测变量(Observation Variables): 这些是可观测的变量,通常是我们直接可以测量或看到的数据。观测变量是状态变量的某种函数加上噪声。
- 状态转移方程(State Transition Equation): 描述状态变量如何随时间变化,通常是前一时刻状态和噪声的函数。
- 观测方程(Observation Equation): 描述观测变量如何由状态变量生成,通常包括状态变量和观测噪声。

3. 应用
结构状态空间模型广泛应用于各种领域,包括但不限于:
- 经济学和金融: 用于经济指标的建模和预测、资产价格建模等。
- 工程和控制系统: 用于系统状态估计、故障检测、自动控制等。
- 生物医学: 用于心脏信号建模、流行病传播建模等。
- 气象学: 用于天气预报和气候建模。
4. 估计和推断
为了使用状态空间模型进行分析,我们通常需要进行以下步骤:
- 参数估计: 估计状态转移矩阵、观测矩阵等参数。这通常通过最大似然估计或贝叶斯方法来完成。
- 状态估计: 给定观测数据,估计状态变量。这通常通过卡尔曼滤波、粒子滤波等方法来完成。
- 预测: 基于估计的状态变量和模型参数,对未来进行预测。
5. 优点
- 灵活性: 可以处理非平稳时间序列,适应不同类型的数据结构。
- 系统性: 能够显式地描述系统的动态特性和观测过程。
- 可解释性: 状态变量和模型参数具有明确的物理意义

图1 选择性SSM概述
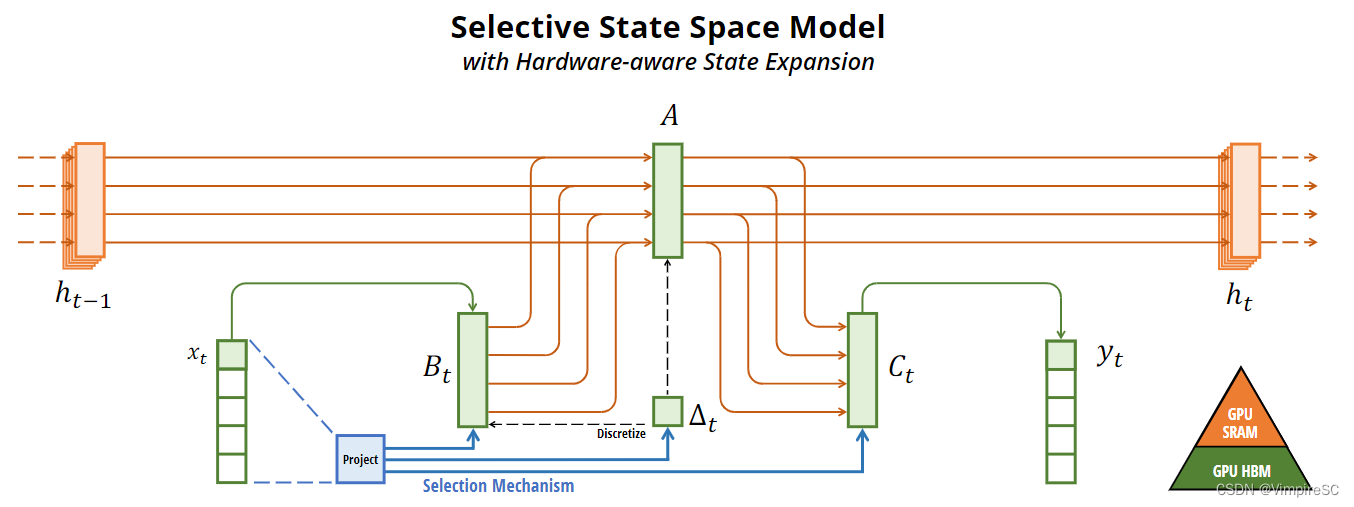
涉及到一种高级的结构化状态空间模型(SSM),以及它如何通过高维潜在状态和巧妙的计算路径来处理多通道输入数据并映射到输出。


离散化方法
定义

符号解释

零阶保持器

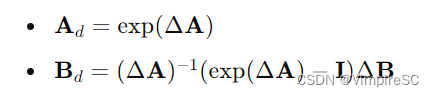
Computation计算

主要内容
一种混合训练和推理策略,该策略在训练和推理过程中使用不同的模式来提高效率。具体来说,这种策略在训练过程中使用并行的卷积模式,而在推理过程中使用递归模式。这种方法结合了卷积神经网络(CNN)和递归神经网络(RNN)的优点,以提高模型的训练效率和推理性能。
卷积如何进行并行操作的
卷积算法并行编程原理是通过将卷积操作划分为多个小的并行任务,利用多个处理单元同时计算,以加速卷积计算的过程。
并行编程的原理可以基于多种不同的架构和编程模型。以下是几种常见的卷积算法并行编程原理:
-
数据并行:将输入数据划分为多个部分,每个处理单元负责处理一部分数据。这种方式适用于多核CPU或GPU等多处理器架构。每个处理单元独立计算局部卷积,最后将结果合并得到最终的卷积结果。
-
线程并行:使用线程来并行执行卷积操作。这种方式适用于支持线程并行的多核CPU或GPU。每个线程负责处理输入数据的一部分,并独立计算局部卷积。通过合并各个线程的计算结果,得到最终的卷积结果。
-
图像并行:将输入图像划分为多个较小的块,并将每个块分配给不同的处理核心进行独立计算。这种方式适用于处理大尺寸的图像。每个处理核心独立计算局部卷积,并将结果合并得到最终的卷积结果。
-
指令级并行:利用SIMD(单指令多数据)指令集来实现并行计算。通过同时处理多个数据元素,以提高运算速度。这种方式适用于支持SIMD指令集的处理器。通过对输入数据进行向量化操作,实现并行计算。
在实际应用中,我们可以根据具体的硬件架构和编程模型选择适合的并行编程原理,并结合优化技术,如数据重用、内存局部性等,进一步提高卷积算法的并行性能。
卷积和递归有什么不同?
递归概念及优缺点

卷积概念及优缺点

不同之处
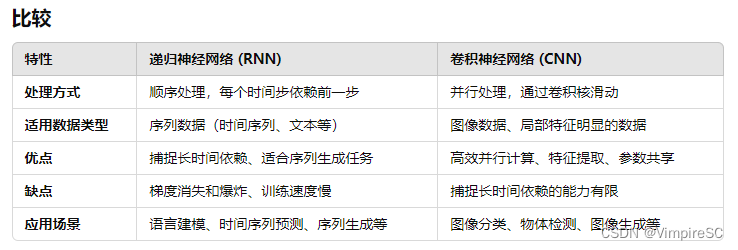
推理模式使用递归的好处

线性时间不变性(LTI)
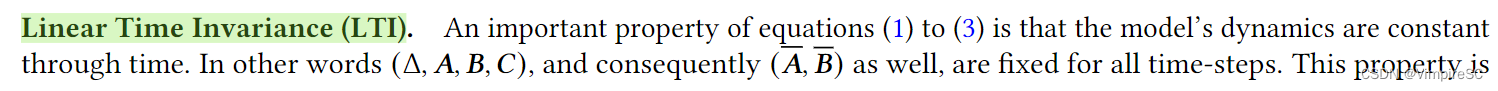

探讨了模型动力学随时间保持恒定的重要性质,即线性时不变性(LTI)
线性时不变性(LTI):
方程1-3
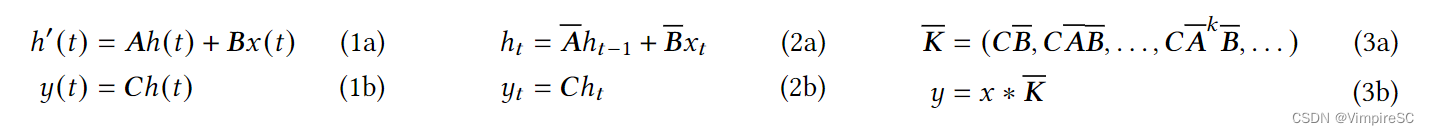

LTI在本文概念、LTI模型的局限性和作者对于LIT模型的改进

结构及尺寸

讨论了结构化SSM(结构化状态空间模型)的命名原因和其特定的结构化形式,重点是如何有效地计算这些模型

一般空间状态模型

讨论了“状态空间模型”(State Space Model, SSM)这一术语在不同领域中的广泛含义,以及该论文中对这一术语的具体使用


S4模型

SSM体系结构
- 介绍SSM及其在神经网络中的应用,强调其独特性和灵活性。
- 讨论几种著名的SSM架构及其特点,展示SSM在不同任务中的应用。
- 提到其他密切相关的SSM和架构,并将在扩展的相关工作中进一步讨论这些方法。
解释了状态空间模型(SSM)及其在现代神经网络架构中的应用。

1.讲述了 SSM的独立性和端到端性
2.SSNN又可以叫SSM,结构化状态空间神经网络,可以多层处理

介绍了一些著名的SSM架构,如线性注意力、H3结构、Hyena结构、Retnet和RWKV


3 Selective State Space Models
讨论了论文中的研究流程和主要贡献,尤其是选择机制如何被纳入状态空间模型(SSM),并解决了由此带来的计算挑战。
对每一个章节的介绍

第3.1节和3.2节内容
3.1节:通过合成任务来激励理解选择机制
3.2节:解释如何将选择机制纳入状态空间模型以及引入了时变SSM(动态参数在时间上是变化的)

第3.3节、3.4节和3.5节内容
3.3节:因为时变SSM不能卷积,改进硬件提出硬件感知算法
3.4节:一种无需注意力机制和MLP块的SSM架构
3.5节:讨论文鲁棒性、可解释性和泛化性,以及对模型进行优化

3.1 Motivation:Selection as a Means of Compression
动机:选择作为一种压缩手段
下面一段探讨了序列建模中的一个基本问题,即如何将上下文信息压缩到较小的状态。这种压缩在不同的序列模型中呈现出不同的权衡和挑战。

序列模型上下文压缩问题
序列建模中的一个重要权衡在于如何有效地压缩和存储上下文信息。
注意力机制和递归模型各有优缺点:
1.注意力机制:能够灵活捕捉上下文,但需要大量内存和计算资源。
2.递归模型:在效率上有优势,但其有限的状态容量可能限制其对长序列的处理能力。

合成任务(为理解压缩推理原理)
解释了为了理解上下文压缩和推理的原理,研究者们使用了两个合成任务的运行示例。
这些任务被设计来测试和展示模型在不同情况下处理和记住上下文信息的能力。

合成任务解释

合成任务的目的和意义
序列模型局限性特殊情况(失效模式)
深入探讨了序列模型的局限性,特别是线性时不变(LTI)模型在处理某些任务时的失效模式,并引出了一种新的构建原则,即选择性。

递归模型和卷积模型的局限性
递归模型:状态更新规则不变,难以根据动态调整
卷积模型:在选择任务中不佳,缺乏内容感知,输入到输出间隔是变化的,无法有效建模

状态压缩的权衡及选择性机制的提出
状态压缩:为了高效,有效处理记住上下文信息。需要较小的状态及包含所有必要信息的状态
选择性机制:为了克服上述局限性,提出选择性机制


序列维度的传播与交互定义
信息在递归时候,通过时间步传播。在卷积模型,通过卷积进行传播

序列的交互通过自注意机制去聚合或通过门控机制决定哪些信息可以传递或丢弃

3.2 Improving SSMs with Selection通过选择改进SSM
解释了如何将选择机制整合到模型中,并指出了这种整合对模型效率的影响。

选择机制的整合
在RNN中动态调整动力学参数,在CNN中动态调整卷积核参数

从时不变到时变性的转换
改为时变性,模型可以动态调整参数,但是失去卷积效率。

描述参数及函数
描述了选择机制中的具体参数化方法,详细说明了如何使用线性投影和激活函数来实现这些选择机制

设计三个线性投影和一个激活函数
一个参数化的线性投影函数,一个广播操作,一个激活函数

四个选择机制,两个将x投影到维度N上得到B和C,两个机制将x投影到维度1,然后广播到D上。

RNN的门控机制GRU如下网址所示
9.1. 门控循环单元(GRU) — 动手学深度学习 2.0.0 documentation
图2
Figure 2 指的是三个合成任务示例,这些任务展示了不同类型的序列建模问题以及不同模型在解决这些问题时的挑战和要求。
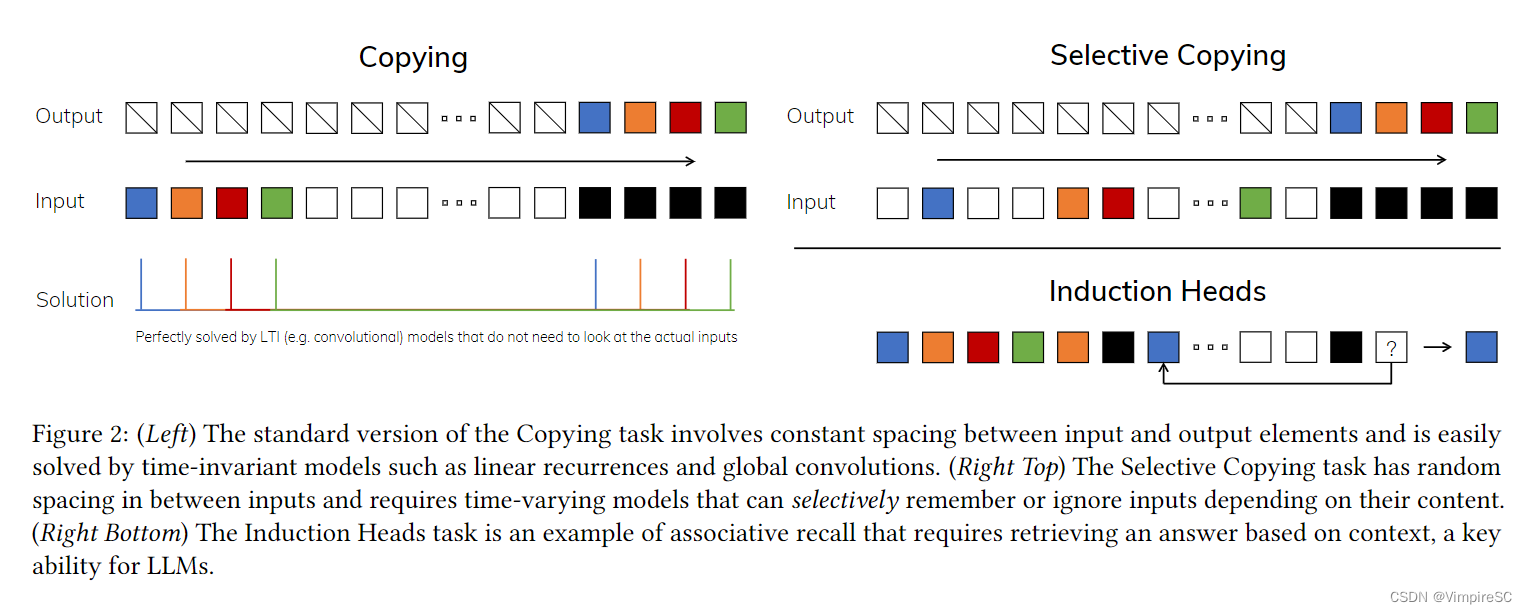
复制任务
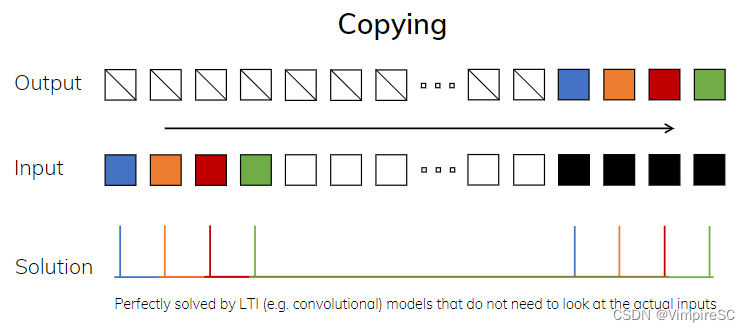

选择性复制任务
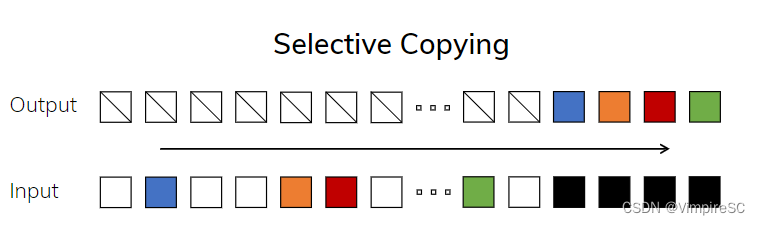

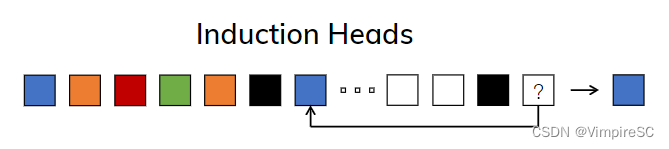
归纳头任务

算法流程图
这里给出了两个算法,分别是 SSM (S4) 和 SSM + Selection (S6)。它们描述了结构化状态空间模型(SSM)在处理输入序列 声明:本文内容由网友自发贡献,转载请注明出处:【wpsshop】
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。



