- 1Android——最强大的RecyclerView框架
- 2Flink集成kafka消费数据和推送消息_flink 推送
- 3lstm 文本纠错_PyCorrector文本纠错工具实践和代码详解
- 4【面试题】手写Promise_面试题手写一个promise代码
- 5J204B接口简介
- 6数据结构:顺序表的实现
- 7KVM IO虚拟化_virtualio和virtual bus
- 8用Python的flask、tornado和fastapi探索SSE推送服务_flask sse
- 92024年运维最新dbeaver安装和使用教程_dbeaver使用教程,2024年最新透彻解析
- 10el-select的错误提示不生效、el-select验证失灵、el-select的blur规则失灵_elementplus el-select v-model placeholder 不生效
数据结构与算法之决策树算法_决策树数据结构
赞
踩
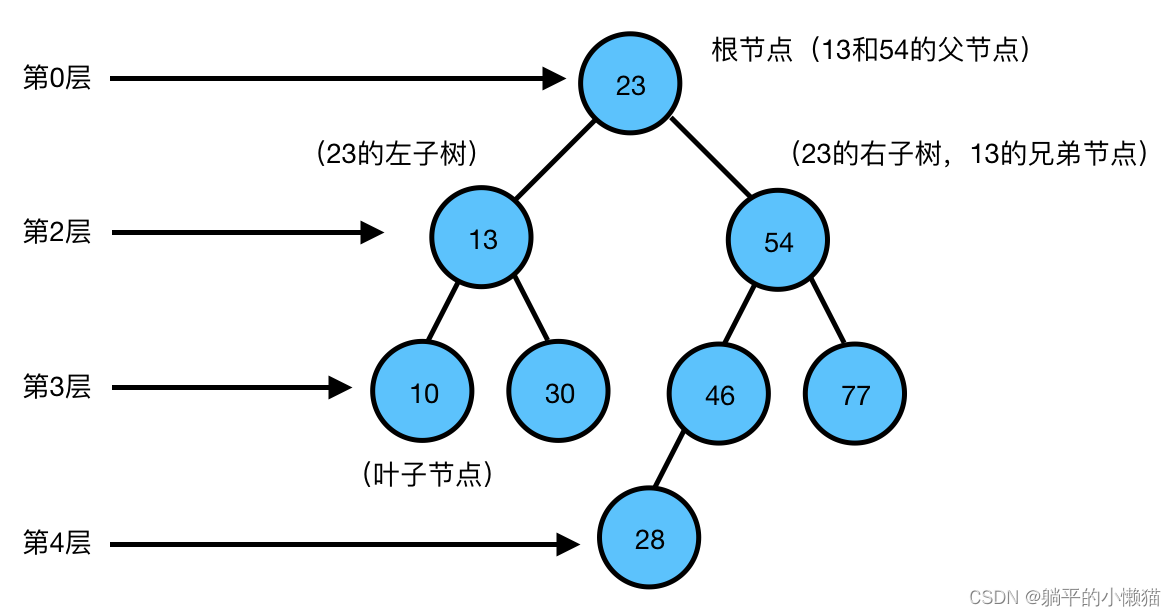
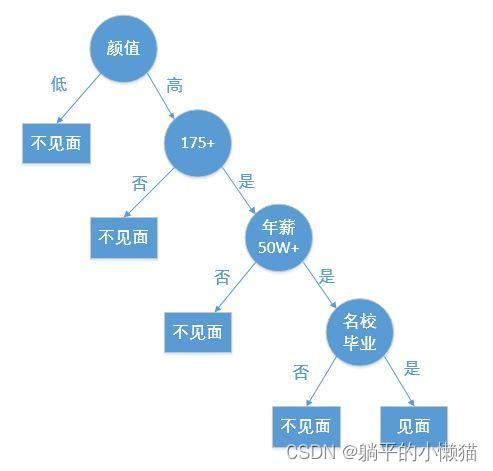
决策树算法是一种基于树形结构的分类和回归分析方法,其基本思想是将数据集分成一些小的子集,每个子集都对应着某个决策条件。通过对数据集的分解和判断,不断对决策条件进行选择,最终达到分类和回归的目的。
决策树算法的基本原理包括:
-
节点选择:决策树的构建是一个递归过程,每次需要选择一个最佳的特征来作为分裂节点。常用的特征选择方法有信息增益、信息增益比和基尼不纯度等。
-
剪枝:决策树容易出现过拟合现象,因此需要采取剪枝操作来避免决策树的过度复杂化。剪枝的方法包括预剪枝和后剪枝两种。
-
分类预测:决策树构建完成后,可以用于分类和回归分析。对于新的数据样本,可根据决策树的规则进行判断和预测。
决策树算法具有易于理解和解释,分类效果较好等优点。在实际应用中,可以用于医学诊断、金融风险评估、电商推荐等方面。但该算法也存在容易受数据噪声影响、易于过拟合等缺点,因此在实际使用中需要注意数据预处理和模型调优等问题。

一、C 实现决策树算法及代码详解
决策树算法是一种常用的分类算法,其中树上的每个节点都对应着一个问题,根据不同的问题选取不同的属性进行划分,直至到叶节点为止。下面我们通过C语言来实现决策树算法,并详细解释其实现过程。
一、决策树算法的实现流程
1.读入数据集
2.计算数据集中各个属性的信息熵
3.根据信息增益最大的属性划分当前数据集
4.递归划分各个子数据集,直到满足结束条件
5.构建决策树模型
二、决策树算法的代码实现
1.读入数据集
我们需要将训练数据集存储在一个CSV文件中,然后将其读入程序中。例如,我们有如下的训练集:
| 年龄 | 收入 | 学历 | 是否购买 |
|---|---|---|---|
| 青年 | 高 | 大专 | 否 |
| 青年 | 高 | 本科 | 否 |
| 中年 | 高 | 本科 | 是 |
| 老年 | 中 | 本科 | 是 |
| 老年 | 低 | 中专 | 是 |
| 中年 | 低 | 大专 | 否 |
| 青年 | 中 | 大专 | 是 |
将其保存为“train.csv”文件,然后通过如下代码读入:
#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX_DATA_NUM 1000 #define MAX_LINE_LEN 1024 // 训练数据 typedef struct train_data_t { char* age; char* income; char* education; char* buy; } train_data_t; // 读取训练数据 int readTrainData(train_data_t* data, char* filePath, int maxNum) { FILE* fp; char line[MAX_LINE_LEN] = { 0 }; char* ret = NULL; int index = 0; fp = fopen(filePath, "r"); if (fp == NULL) { printf("can not open file %s\n", filePath); return -1; } // 读取训练数据 while (fgets(line, MAX_LINE_LEN, fp) != NULL) { if (index >= maxNum) { break; } // 解析训练数据 ret = strtok(line, ","); data[index].age = strdup(ret); ret = strtok(NULL, ","); data[index].income = strdup(ret); ret = strtok(NULL, ","); data[index].education = strdup(ret); ret = strtok(NULL, ","); data[index].buy = strdup(ret); ++index; } fclose(fp); return index; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
2.计算数据集中各个属性的信息熵
在决策树算法中,信息熵是用来衡量数据的不确定性的指标。计算信息熵的公式为:
H = − ∑ i = 1 n p i log 2 p i H = -\sum\limits_{i=1}^n p_i\log_2p_i H=−i=1∑npilog2pi
其中, n n n表示数据集中的分类数, p i p_i pi表示某一分类在数据集中出现的概率。
在C语言中,可以通过如下代码来计算信息熵:
// 计算信息熵 double calcEntropy(train_data_t* data, int num) { int buyCount[2] = { 0 }; double buyProp[2] = { 0.0 }; double entropy = 0.0; int i; // 统计是否购买的数量 for (i = 0; i < num; ++i) { if (strcmp(data[i].buy, "是") == 0) { ++buyCount[1]; } else { ++buyCount[0]; } } // 计算是否购买的概率 buyProp[0] = (double)buyCount[0] / num; buyProp[1] = (double)buyCount[1] / num; // 计算信息熵 for (i = 0; i < 2; ++i) { if (buyProp[i]) { entropy -= buyProp[i] * log2(buyProp[i]); } } return entropy; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
3.根据信息增益最大的属性划分当前数据集
信息增益是表示划分后数据集的不确定性减少的程度,计算公式为:
I G ( D , A ) = H ( D ) − ∑ v ∈ V ∣ D v ∣ ∣ D ∣ H ( D v ) IG(D, A) = H(D) - \sum\limits_{v\in V} \frac{|D^v|}{|D|} H(D^v) IG(D,A)=H(D)−v∈V∑∣D∣∣Dv∣H(Dv)
其中, D D D表示当前数据集, V V V表示某一属性的取值集合, D v D^v Dv表示满足属性值为 v v v的子集, H ( D ) H(D) H(D)表示当前数据集的信息熵。
可以通过如下代码计算属性的信息增益:
// 计算信息增益 double calcInfoGain(train_data_t* data, int num, int attrIndex, double parentEntropy) { char* attrValues[MAX_DATA_NUM] = { 0 }; int valuesCount[MAX_DATA_NUM] = { 0 }; int valuesNum = 0; train_data_t* dataPtrs[MAX_DATA_NUM] = { 0 }; int dataCounts[MAX_DATA_NUM] = { 0 }; int dataNums[MAX_DATA_NUM] = { 0 }; double entropySum = 0.0; double infoGain = 0.0; int i, j; // 统计各个属性的取值 for (i = 0; i < num; ++i) { int found = 0; for (j = 0; j < valuesNum; ++j) { if (attrValues[j] && strcmp(attrValues[j], data[i].age) == 0) { ++valuesCount[j]; found = 1; break; } } if (!found) { attrValues[valuesNum] = strdup(data[i].age); valuesCount[valuesNum] = 1; ++valuesNum; } } // 统计各个属性取值的数据 for (i = 0; i < valuesNum; ++i) { for (j = 0; j < num; ++j) { if (strcmp(attrValues[i], data[j].age) == 0) { dataPtrs[i * MAX_DATA_NUM + dataCounts[i]] = &data[j]; ++dataCounts[i]; } } dataNums[i] = dataCounts[i]; } // 计算信息熵 for (i = 0; i < valuesNum; ++i) { double entropy = 0.0; entropy = calcEntropy(dataPtrs + i * MAX_DATA_NUM, dataCounts[i]); entropySum += (double)dataCounts[i] / num * entropy; } // 计算信息增益 infoGain = parentEntropy - entropySum; return infoGain; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
4.递归划分各个子数据集,直到满足结束条件
我们递归地对每一个子数据集进行划分,直至到满足某一个结束条件。例如,在这里我们可以设置决策树最大的深度或者划分后数据集中的某个分类样本数目小于某个阈值等条件作为结束条件。
以下是递归划分数据集的代码:
// 划分数据集 node_t* splitData(train_data_t* data, int num, double parentEntropy, int depth, int maxDepth) { node_t* node = NULL; int attrIndex = -1; double infoGainMax = -1.0; int i; // 判断是否满足结束条件 if (num == 0 || depth == maxDepth) { return NULL; } // 计算信息增益最大的属性索引 for (i = 0; i < ATTR_NUM; ++i) { double infoGain = calcInfoGain(data, num, i, parentEntropy); if (infoGainMax < infoGain) { infoGainMax = infoGain; attrIndex = i; } } // 判断是否满足结束条件 if (infoGainMax < 0 || attrIndex < 0) { return NULL; } // 构建节点 node = (node_t*)malloc(sizeof(node_t));
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
二、C++ 实现决策树算法及代码详解
决策树是一种基于树结构的分类模型,它可以对特征空间进行划分,从而将样本集合划分为不同的类别。本篇文章将介绍如何使用C++实现决策树算法,并提供详细的代码解释。
首先,我们需要定义一个节点结构体来表示决策树的节点。
struct Node {
int feature; // 特征编号
bool is_leaf; // 是否为叶节点
std::string label; // 分类标签
Node* left; // 左子节点指针
Node* right; // 右子节点指针
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
我们在结构体中定义了五个成员变量:特征编号、是否为叶节点、分类标签以及左右子节点指针。其中,特征编号是用于表示该节点所选择的划分特征,分类标签则是用于表示该节点的类别。
接下来是决策树的训练过程。我们采用递归的方式来构建决策树,其中需要用到ID3算法或C4.5算法对特征空间进行划分。
Node* build_tree(std::vector<std::vector<std::string>> data, std::vector<std::string> features) { Node* node = new Node(); node->label = get_majority_class(data); if (data.size() == 1) { node->is_leaf = true; return node; } if (features.empty()) { node->is_leaf = true; return node; } if (is_same_class(data)) { node->is_leaf = true; node->label = data[0].back(); return node; } int best_feature = get_best_feature(data, features); node->feature = best_feature; node->is_leaf = false; node->left = build_tree(get_small_subset(data, best_feature, true), get_subset(features, best_feature)); node->right = build_tree(get_small_subset(data, best_feature, false), get_subset(features, best_feature)); return node; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
其中,get_majority_class函数用于获取当前样本集合中占比最多的类别;is_same_class函数用于判断当前样本集合是否属于同一类别;get_best_feature函数用于获取最佳划分特征;get_small_subset函数用于根据特征的取值划分子集;get_subset函数用于更新特征集合。
接下来是决策树的预测过程,即对新数据进行分类。我们同样采用递归的方式来对数据进行分类。
std::string predict(Node* node, std::vector<std::string> sample) {
if (node->is_leaf) {
return node->label;
}
int feature = node->feature;
if (sample[feature] == "1") {
return predict(node->left, sample);
} else {
return predict(node->right, sample);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
最后,我们将构建好的决策树和测试数据输入到程序中,即可得到分类结果。
std::vector<std::vector<std::string>> data = {{"0", "0", "0", "1", "no"},
{"0", "0", "1", "1", "yes"},
{"1", "0", "0", "1", "yes"},
{"1", "1", "1", "1", "no"},
{"0", "1", "0", "0", "yes"},
{"0", "1", "1", "0", "no"}};
std::vector<std::string> features = {"0", "1", "2", "3"};
Node* root = build_tree(data, features);
std::vector<std::string> sample = {"1", "0", "1", "0"};
std::cout << predict(root, sample) << std::endl;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
以上就是C++实现决策树算法的全部代码和详解。
三、Java 实现决策树算法及代码详解
决策树算法是一种基于树形结构的分类算法,它通过对数据集进行分割,得到一棵树,每个节点表示一个分类条件(属性),分支表示该条件下的不同取值,最终叶子节点所代表的分类就是该数据的分类。
下面是 Java 实现决策树算法的步骤及代码详解:
- 定义数据结构
决策树算法的核心是树形结构,因此我们需要定义树节点数据结构。在本实现中,我们使用一个类来表示树节点,其中包含以下属性:
- feature:分类条件(属性)名称
- label:叶子节点的分类标签
- children:子节点列表
- value:当前节点的取值
代码如下:
public class TreeNode {
private String feature;
private String label;
private List<TreeNode> children;
private String value;
// constructors, getters and setters
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 定义决策树算法
决策树的生成过程可以使用递归实现,具体步骤如下:
- 如果数据集已经完全属于同一类别,则返回该类别作为叶子节点的分类结果;
- 如果数据集中只剩下一个特征,将数据集中出现次数最多的类别作为叶子节点的分类结果;
- 选择最优特征,将数据集分成子集,对每个子集递归调用本算法,直到所有特征被使用或子集中的实例属于同一类别。
在本实现中,我们使用信息熵(熵越小表示样本更加纯净)和信息增益(增益越大表示该特征对分类的贡献越大)来评估每个特征的重要性,选取信息增益最大的特征作为分类条件。具体代码如下:
public TreeNode buildDecisionTree(List<String[]> data, List<String> features) { // 1. 如果数据集已经完全属于同一类别,则返回该类别作为叶子节点的分类结果 if (isSameClass(data)) { String label = data.get(0)[data.get(0).length - 1]; return new TreeNode(null, label, null, null); } // 2. 如果数据集中只剩下一个特征,将数据集中出现次数最多的类别作为叶子节点的分类结果 if (features.size() == 1) { String label = findMostCommonClass(data); return new TreeNode(null, label, null, null); } // 3. 选择最优特征,将数据集分成子集,对每个子集递归调用本算法 String bestFeature = findBestFeature(data, features); TreeNode root = new TreeNode(bestFeature, null, new ArrayList<>(), null); features.remove(bestFeature); Map<String, List<String[]>> subsets = splitData(data, bestFeature); for (Map.Entry<String, List<String[]>> entry : subsets.entrySet()) { String value = entry.getKey(); List<String[]> subset = entry.getValue(); if (subset.isEmpty()) { String label = findMostCommonClass(data); root.getChildren().add(new TreeNode(null, label, null, value)); } else { TreeNode child = buildDecisionTree(subset, new ArrayList<>(features)); child.setValue(value); root.getChildren().add(child); } } features.add(bestFeature); return root; } // 判断数据集是否属于同一类别 private boolean isSameClass(List<String[]> data) { String firstClass = data.get(0)[data.get(0).length - 1]; for (int i = 1; i < data.size(); i++) { if (!firstClass.equals(data.get(i)[data.get(i).length - 1])) { return false; } } return true; } // 找出数据集中出现次数最多的类别 private String findMostCommonClass(List<String[]> data) { Map<String, Integer> countMap = new HashMap<>(); for (String[] instance : data) { String label = instance[instance.length - 1]; countMap.put(label, countMap.getOrDefault(label, 0) + 1); } String mostCommonLabel = null; int maxCount = 0; for (Map.Entry<String, Integer> entry : countMap.entrySet()) { if (entry.getValue() > maxCount) { mostCommonLabel = entry.getKey(); maxCount = entry.getValue(); } } return mostCommonLabel; } // 找出最优特征 private String findBestFeature(List<String[]> data, List<String> features) { double entropy = calculateEntropy(data); double maxGain = -1; String bestFeature = null; for (String feature : features) { double featureEntropy = 0; Map<String, List<String[]>> subsets = splitData(data, feature); for (Map.Entry<String, List<String[]>> entry : subsets.entrySet()) { List<String[]> subset = entry.getValue(); double subsetEntropy = calculateEntropy(subset); double weight = (double) subset.size() / data.size(); featureEntropy += weight * subsetEntropy; } double gain = entropy - featureEntropy; if (gain > maxGain) { maxGain = gain; bestFeature = feature; } } return bestFeature; } // 计算信息熵 private double calculateEntropy(List<String[]> data) { Map<String, Integer> countMap = new HashMap<>(); for (String[] instance : data) { String label = instance[instance.length - 1]; countMap.put(label, countMap.getOrDefault(label, 0) + 1); } double entropy = 0; for (Map.Entry<String, Integer> entry : countMap.entrySet()) { double p = (double) entry.getValue() / data.size(); entropy -= p * Math.log(p) / Math.log(2); } return entropy; } // 将数据集按特征分成多个子集 private Map<String, List<String[]>> splitData(List<String[]> data, String feature) { Map<String, List<String[]>> subsets = new HashMap<>(); for (String[] instance : data) { String value = instance[getKeyIndex(feature)]; List<String[]> subset = subsets.getOrDefault(value, new ArrayList<>()); subset.add(instance); subsets.put(value, subset); } return subsets; } // 根据特征名称找到它在数据集中的下标 private int getKeyIndex(String key) { String[] header = this.data.get(0); for (int i = 0; i < header.length; i++) { if (header[i].equals(key)) { return i; } } return -1; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 使用决策树进行分类
得到决策树后,我们可以使用它对新的实例进行分类。具体步骤如下:
- 对于每个节点,比较实例的属性值和节点的取值,如果相同,则遍历该节点的子树;
- 如果遍历到叶子节点,返回该节点的分类标签。
在本实现中,我们使用递归实现决策树的分类过程,具体代码如下:
public String classify(String[] instance) { return classify(instance, root); } private String classify(String[] instance, TreeNode node) { if (node.getChildren().isEmpty()) { // 叶子节点,返回分类标签 return node.getLabel(); } else { for (TreeNode child : node.getChildren()) { if (child.getValue().equals(instance[getKeyIndex(node.getFeature())])) { return classify(instance, child); } } } return null; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 测试代码
最后,我们编写一个测试代码,读入数据集(本实现中使用的是鸢尾花数据集),使用 5 折交叉验证测试决策树算法的分类准确率。具体代码如下:
public static void main(String[] args) throws IOException {
List<String[]> data = loadCsvFile("iris.csv");
int k = 5;
double sumAccuracy = 0;
List<List<String[]>> folds = splitDataIntoKFolds(data, k);
for (int i = 0; i < k; i++) {
List<String[]> trainData = new ArrayList<>();
List<String[]> testData = folds.get(i);
for (int j = 0; j < k; j++) {
if (j != i) {
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10





