聚类分析|基于密度的聚类方法DBSCAN及其Python实现

0. 基于密度的聚类方法

之前介绍过基于划分的聚类算法，如k-means和k-medoids，也介绍过基于层次聚类的方法。这两种方法本质上都是基于距离的算法，只能发现类圆形的聚类。

基于密度的方法（Density-based Methods）是基于密度的，可以克服基于距离的算法只能发现“类圆形”聚类的缺点。
主要思想：只要在给定半径邻近区域的密度超过某个阈值，就把它添加到与之相近的簇类中去。
这样的方法可以用来过滤噪声数据，并且可以发现任意形状的聚类。
基于密度的方法中，代表算法有：

• DBSCAN算法
• OPTICS算法
• DENCLUE算法
  以下对DBSCAN（Density Based Spatial Clustering of Applications with Noise，DBSCAN）聚类算法进行介绍。

1. DBSCAN聚类算法的相关概念

DBSCAN是基于密度聚类中的经典算法，突出特色在于：

• 第一，利用小类的密度可达性（或称连通性），可发现任意形状的小类
• 第二，聚类同时可以发现数据中的噪声，也即离群点

DBSCAN聚类中有两个重要参数：

1. 邻域半径$\epsilon$；
2. 邻域半径$\epsilon$范围内包含的最少观测点个数，记为$minPts$。

基于这两个参数，DBSCAN聚类将样本观测点分成以下4类：

1. 核心点（核心样本）$P$：若任意样本观测点$O$的邻域半径$\epsilon$内的邻居个数不少于$minPts$，则称$O$为核心点，记作$P$
2. 核心点$P$的直接密度可达点$Q$：若任意样本观测点$Q$在核心点$P$的邻域半径$\epsilon$范围内，则称点$Q$为核心点$P$的直接密度可达点。也称从点$P$直接密度可达点$Q$
3. 核心点$P$的密度可达点$Q$：若存在一系列样本观测点 $O_1,O_2,\dots ,O_n$，且$O_{i+1}(i=1,2,...,n-1)$是$O_i$的直接密度可达点，且$O_i=P,O_n=Q$，则称$Q$是点$P$的密度可达点，也称从点$P$密度可达点$Q$。
4. 噪声点：除上述类型之外的样本观测点，均定义为噪声点。
   如下图所示，$q$是一个核心样本，$p$由$q$直接密度可达。
   

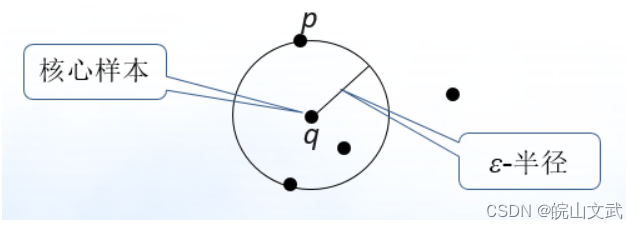
• 直接密度可达的传递性会导致密度可达！
• 若存在任意样本观测点$O$，同时密度可达点$O_1$和点$O_2$，则称点$O_1$和点$O_2$是密度相连的。

2. DBSCAN聚类过程

设置邻域半径$\epsilon$和邻域半径$\epsilon$范围内包含的最少观测点个数$minPts$。
在参数设定的条件下，DBSCAN聚类过程大致包括形成小类和合并小类两个阶段：

2.1 形成小类

1. 从任意一个样本观测点$O_i$开始，在参数限定的条件下判断$O_i$是否为核心点。
2. 若$O_i$是核心点，首先标记该点为核心点。然后，找到$O_i$的所有（如$m$个）直接密度可达点（包括边缘点），并形成一个以$O_i$为“核心”的小类，记作$C_i$。$m$个直接密度可达点（尚无小类标签）和样本观测点$O_i$的小类标签均为$C_i$
3. 若$O_i$不是核心点，那么$O_i$可能是其他核心点的直接密度可达点，或密度可达点，亦或噪声点。若$O_i$是直接密度可达点或密度可达点，则一定会在后续的处理中被归到某个小类，带有小类标签$C_j$。若是噪声点，则不会被归到任何小类中，始终不带有小类标签

2.2 合并小类

• 判断带有核心点标签的所有核心点之间，是否存在密度可达和密度相连关系。若存在，则将相应的小类合并起来，并修改相应样本观测点的小类标签

3. DBSCAN算法的Python实现

在scikit-learn中，包含sklearn.cluster.DBSCAN的算法。DBSCAN()常用形式为：

DBSCAN(eps=0.5,min_samples=5,metric=’euclidean’, algorithm=’auto’)
1

参数说明：

1. eps：设置半径，用以确定邻域的大小，默认0.5。
2. min_samples：int，设置阈值MinPts。
3. metric：采用的距离计算方式，默认是欧式距离。
4. algorithm：取值{’auto’,’ball_tree’,’kd_tree’,’brute’}。用于计算两点间距离并找出最近邻的点。取值为：’auto’：由算法自动取舍合适的算法；’ball_tree’：用ball树来搜索；’kd_tree’：用kd树搜索；’brute’：暴力搜索。对于稀疏数据，一般取值’brute’。

3.1 DBSCAN算法示例

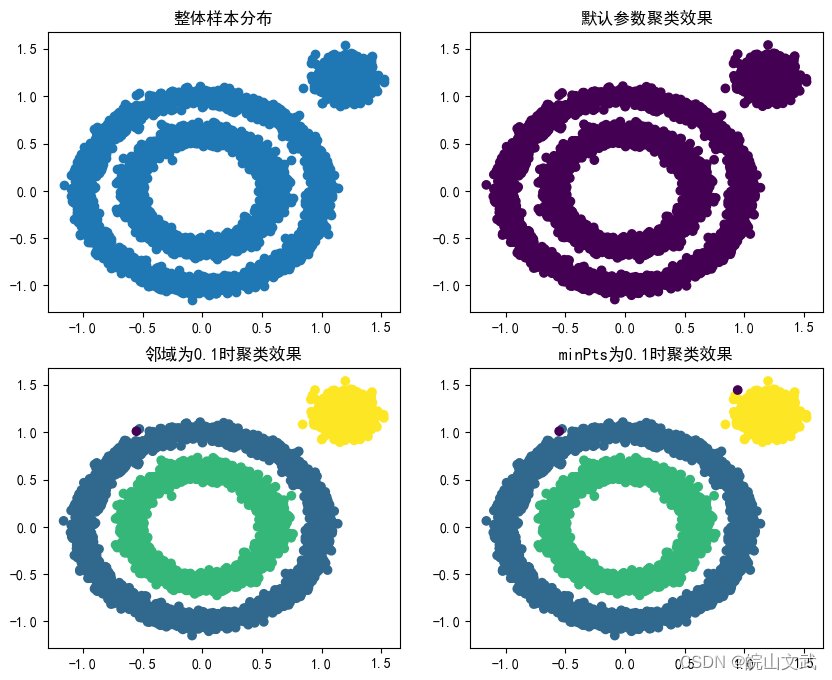
1. 首先生成一组随机数据，为了体现DBSCAN在非凸数据的聚类优点，生成三簇数据，两组是非凸的。
2. 直接使用DBSCAN默认参数，观看聚类效果
3. 对DBSCAN的两个关键的参数eps和min_samples进行调参，当类别数太少，需要增加类别数，那么就可以减少邻域的大小，默认是0.5，下面减到0.1
4. 将min_samples从默认的5增加到10，观看效果。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x1,y1=datasets.make_circles(n_samples=5000, factor=0.6,noise=0.05)
x2,y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9)
x = np.concatenate((x1, x2))
plt.rcParams['font.sans-serif']=['SimHei'] 
plt.rcParams['axes.unicode_minus']=False
plt.figure(figsize=(10,8))
plt.subplot(2,2,1)
# 观察总体样本分布
plt.title("整体样本分布")
plt.scatter(x[:,0],x[:,1], marker='o')
plt.subplot(2,2,2)
# 观察认参数聚类效果
plt.title("默认参数聚类效果")
x = np.concatenate((x1, x2))
y_pred = DBSCAN().fit_predict(x)
plt.scatter(x[:,0],x[:, 1], c=y_pred)
plt.subplot(2,2,3)
# 观察邻域为0.1时聚类效果
plt.title("邻域为0.1时聚类效果")
y_pred2 = DBSCAN(eps = 0.1).fit_predict(x)
plt.scatter(x[:,0],x[:,1],c=y_pred2)
plt.subplot(2,2,4)
# 观察minPts为10时聚类效果
plt.title("minPts为0.1时聚类效果")
y_pred3 = DBSCAN(eps = 0.1,min_samples =10).fit_predict(x)
plt.scatter(x[:,0],x[:,1],c=y_pred3)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

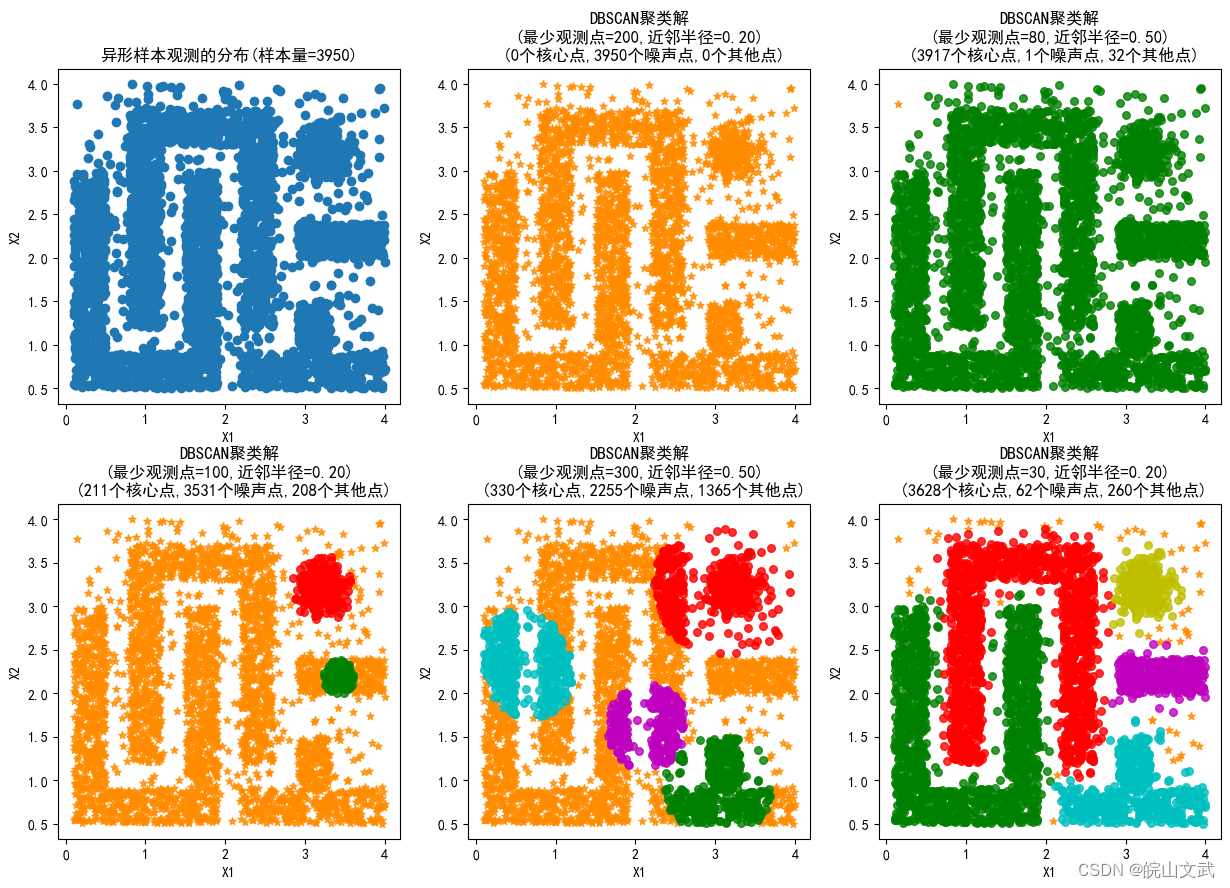
3.2 DBSCAN的异型聚类特点

DBSCAN聚类的最大特点是能够发现任意形状的类。
DBSCAN算法对参数$\epsilon$（邻域半径）和$minPts$极为敏感。以下进行相关参数设置试验以说明特性：

1. 邻域半径$\epsilon$较小，且邻域范围内的最少观测点个数$minPts$较多
2. 邻域半径$\epsilon$较大，且邻域范围内的最少观测点个数$minPts$较少
3. 适中的参数设置

试验代码如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from itertools import cycle
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  
plt.rcParams['axes.unicode_minus']=False
from scipy.stats import norm
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN,Birch,KMeans,estimate_bandwidth,MeanShift
X=pd.read_csv('异形聚类数据.txt',header=0)
fig=plt.figure(figsize=(15,10))
plt.subplot(231)
plt.scatter(X['x1'],X['x2'])
plt.title("异形样本观测的分布(样本量=%d)"%len(X))
plt.xlabel("X1")
plt.ylabel("X2")

colors = 'bgrcmyk'
EPS=[0.2,0.5,0.2,0.5,0.2]
MinS=[200,80,100,300,30]
Gid=1
for eps,mins in zip(EPS,MinS):
    DBS=DBSCAN(min_samples=mins,eps=eps)
    DBS.fit(X)
    labels=np.unique(DBS.labels_)
    Gid+=1
    plt.subplot(2,3,Gid)
    for i,k in enumerate(labels):
        if k==-1:  #噪声点
            c='darkorange'
            m='*'
        else:
            c=colors[i]
            m='o'
        plt.scatter(X.iloc[DBS.labels_==k,0],X.iloc[DBS.labels_==k,1],c=c,s=30,alpha=0.8,marker=m)
    
    plt.title("DBSCAN聚类解\n(最少观测点=%d,近邻半径=%.2f)\n (%d个核心点,%d个噪声点,%d个其他点)"%(mins,eps,len(DBS.components_),
                                                        sum(DBS.labels_==-1),len(X)-len(DBS.components_)-sum(DBS.labels_==-1)))
    plt.xlabel("X1")
    plt.ylabel("X2")
fig.subplots_adjust(hspace=0.3)
fig.subplots_adjust(wspace=0.2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

4. DBSCAN算法的缺点

在DBSCAN算法中，有两个初始参数$\epsilon$（邻域半径）和$minPts$（$\epsilon$邻域最小样本数）需要用户手动设置输入，并且聚类的类簇结果对这两个参数的取值非常敏感，不同的取值将产生不同的聚类结果，其实这也是大多数需要初始化参数聚类算法的弊端。